Навигация
Сумма и произведение двух комплексно сопряженных чисел являются действительными числами
7. Сумма и произведение двух комплексно сопряженных чисел являются действительными числами.
![]()
![]()
Следствие из 7. ![]()
Модулем комплексного числа ![]() называется действительное число вида
называется действительное число вида
![]() .
.
8. Теорема о сопряженном корне.
Если число ![]() является корнем уравнения
является корнем уравнения
![]() (1)
(1)
с действительным коэффициентами a0 , a1 , …, an , то число ![]() также является корнем уравнения (1).
также является корнем уравнения (1).
Извлечение квадратного корня из комплексного числа ![]() . Пусть
. Пусть
![]() ,
,
где x и y – действительные числа. Возводя обе части этого равенства в квадрат, получаем
![]() .
.
Что равносильно системе

Решая эту систему, получаем:
 ;
;  .
.
Таким образом, извлечение корня квадратного из комплексного числа осуществляется по формуле
 .
.
В скобках перед мнимой единицей берется знак плюс, если ![]() , и знак минус, если
, и знак минус, если ![]() .
.
Задача 1. Найдите комплексные корни уравнения ![]() , если:
, если:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
Решение
а) ![]() .
.
Так как ![]() , то это уравнение можно записать в виде
, то это уравнение можно записать в виде ![]() или
или ![]() . Отсюда, раскладывая левую часть на множители, получаем
. Отсюда, раскладывая левую часть на множители, получаем ![]() , откуда
, откуда ![]() ,
, ![]() .
.
б) ![]() .
.
Учитывая, что ![]() , преобразуем это уравнение:
, преобразуем это уравнение: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , откуда
, откуда ![]() ,
, ![]() .
.
в) ![]() .
.
Преобразуем ![]() ,
, ![]() ,
, ![]() , откуда
, откуда ![]() ,
, ![]() .
.
Ответ: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
Задача 2. Найдите x и y, для которых ![]() .
.
Решение
Получим и решим систему двух уравнений:

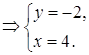
Ответ: ![]() .
.
Задача 3. Решите уравнение ![]() относительно действительных переменных x и y.
относительно действительных переменных x и y.
Решение
Левую часть уравнения можно рассматривать, как некоторое неизвестное комплексное число. Приведя его к виду ![]() , получаем уравнение равносильное данному:
, получаем уравнение равносильное данному: ![]() . Так как два комплексные числа равны тогда и только тогда, когда равны их действительные и мнимые части, приходим к системе:
. Так как два комплексные числа равны тогда и только тогда, когда равны их действительные и мнимые части, приходим к системе:


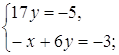

Ответ:  .
.
Задача 4. При каких действительных значениях x и y комплексные числа  и
и ![]() будут противоположными?
будут противоположными?
Решение
Комплексные числа ![]() и
и ![]() будут противоположными, если выполняются условия:
будут противоположными, если выполняются условия:



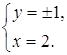
Ответ: ![]() ;
; ![]() .
.
Задача 5. При каких действительных значениях x и y комплексные числа ![]() и
и ![]() будут равными?
будут равными?
Решение
Комплексные числа ![]() и
и ![]() будут равными, если выполняются условия:
будут равными, если выполняются условия:




Ответ: ![]() ;
; ![]() .
.
Задача 6. Решите уравнение ![]() относительно действительных переменных x и y.
относительно действительных переменных x и y.
Решение
Левую часть уравнения можно рассматривать, как некоторое неизвестное комплексное число. Приведя его к виду ![]() , получаем уравнение равносильное данному:
, получаем уравнение равносильное данному: ![]() . Так как два комплексные числа равны тогда и только тогда, когда равны их действительные и мнимые части, приходим к системе:
. Так как два комплексные числа равны тогда и только тогда, когда равны их действительные и мнимые части, приходим к системе:

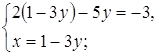


Ответ:  .
.
Задача 7. Решите во множестве комплексных чисел уравнение ![]() .
.
Решение
Так как ![]() , тогда корни находятся по формуле
, тогда корни находятся по формуле
![]() (
(![]() ).
).
Отсюда, ![]() ,
, ![]() .
.
Ответ: ![]() .
.
Задача 8. Решите уравнение ![]() .
.
Решение
Перепишем уравнение в виде ![]() .
.
Полагая ![]() , получим уравнение
, получим уравнение ![]() , которое имеет корень
, которое имеет корень ![]() . Поэтому левую часть этого уравнения можно представить в виде произведения двучлена
. Поэтому левую часть этого уравнения можно представить в виде произведения двучлена ![]() и квадратного трехчлена.
и квадратного трехчлена.
Для нахождения коэффициентов квадратного трехчлена применим схему Горнера:
| 1 | 1 | 2 | – 4 | |
| 1 | 1 | 2 | 4 | 0 |
Итак, получаем уравнение ![]() .
.
Квадратный трехчлен ![]() имеет корни
имеет корни ![]() и
и ![]() .
.
Следовательно, исходное уравнение имеет корни: ![]() ,
, ![]() ,
, ![]() .
.
Ответ: ![]() ;
; ![]() .
.
Задача 9. Решите уравнение ![]() .
.
Решение
Корни данного уравнения находятся по формулам
![]() ,
, ![]() ,
,
где ![]() и
и ![]() – числа, удовлетворяющие условию
– числа, удовлетворяющие условию ![]() . Отсюда
. Отсюда ![]() . Пусть
. Пусть ![]() , тогда
, тогда ![]() , т. е.
, т. е. ![]() . Два комплексных числа равны, следовательно, равны их действительные и мнимые части:
. Два комплексных числа равны, следовательно, равны их действительные и мнимые части:
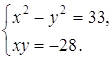
Находим два решения этой системы: ![]() ,
, ![]() . Таким образом,
. Таким образом,
решениями исходного уравнения являются числа ![]() , и
, и
![]() , т. е.
, т. е. ![]() ,
, ![]() .
.
Ответ: ![]() ;
; ![]() .
.
Задача 10. Произведите действия с комплексными числами в алгебраической форме:
а) ![]() ; б)
; б)  ; в)
; в)  .
.
Решение
а) 
б) 
в)

Ответ: а) ![]() ; б)
; б)  ; в)
; в) ![]() .
.
Задача 11. Произведите следующие действия над комплексными числами:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Решение
а) ![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
г)  .
.
Ответ: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Задача 12. Запишите комплексное число  в виде
в виде ![]() .
.
Решение
Имеем

Ответ: ![]() .
.
Задача 13. Найдите значение функции ![]() при
при ![]() .
.
Решение
Подставим значение x в функцию:
![]() .
.
Вычислим второе слагаемое:
 .
.
Вычислим первое слагаемое:
![]() .
.
Таким образом, ![]() .
.
Ответ: ![]() .
.
Задача 14. Вычислите ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Решение
С помощью формулы: 
![]()
Легко получаем:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Ответ: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Задача 15. Выполните указанные действия:  .
.
Решение
Вычислим значение дроби  .
.
Следовательно, 
Ответ: ![]() .
.
Задача 16. Решите уравнение ![]() .
.
Решение
По формуле  , находим:
, находим:
![]() .
.
Заметим, что найденные в этой задаче корни являются сопряженными: ![]() и
и ![]() . Найдем сумму и произведение этих корней:
. Найдем сумму и произведение этих корней: ![]() ,
, ![]() . Число 4 – это второй коэффициент уравнения
. Число 4 – это второй коэффициент уравнения ![]() , взятый с противоположным знаком, а число 13 – свободный член, то есть в этом случае справедлива теорема Виета. Она справедлива для любого квадратного уравнения: если
, взятый с противоположным знаком, а число 13 – свободный член, то есть в этом случае справедлива теорема Виета. Она справедлива для любого квадратного уравнения: если ![]() и
и ![]() – корни уравнения
– корни уравнения ![]() , где
, где ![]() ,
, ![]() .
.
Ответ: ![]() .
.
Задача 17. Составьте приведенное квадратное уравнение с действительными коэффициентами, имеющий корень ![]() .
.
Решение
Второй корень ![]() уравнения является числом, сопряженным с данным корнем
уравнения является числом, сопряженным с данным корнем ![]() , то есть
, то есть ![]() . По теореме Виета находим
. По теореме Виета находим
![]() ;
; ![]() ,
,
где число 2 – это второй коэффициент уравнения, взятый с противоположным знаком, а число 5 – свободный член. Таким образом, получаем уравнение
![]() .
.
Ответ: ![]() .
.
Задача 18. Даны числа ![]() ;
; ![]() . Найдите:
. Найдите:
а)![]() ; б)
; б) ![]() .
.
Решение
а) ![]() , тогда
, тогда
![]()
б) ![]() , тогда
, тогда
 Ответ: а)
Ответ: а) ![]() ; б)
; б) ![]() .
.
Задача 19. Зная, что корнем уравнения ![]() является число
является число ![]() , найдите все корни данного уравнения.
, найдите все корни данного уравнения.
Решение
Поскольку все коэффициенты данного уравнения – действительные числа, то на основании теоремы о сопряженном корне, делаем вывод, что число ![]() также является корнем данного уравнения.
также является корнем данного уравнения.
Пусть ![]() – неизвестный корень уравнения
– неизвестный корень уравнения ![]() , тогда
, тогда ![]() , где
, где
![]() , получаем
, получаем ![]() .
.
Разделим обе части последнего равенства на ![]() , получим
, получим ![]() .
.
Следовательно, ![]() .
.
Ответ: ![]() ;
; ![]() .
.
Задача 20. Найдите все комплексные числа, каждое из которых сопряжено со своим квадратом.
Решение
Пусть ![]() – искомое комплексное число, где x и y – действительные числа. Тогда число
– искомое комплексное число, где x и y – действительные числа. Тогда число ![]() , сопряженное числу
, сопряженное числу ![]() , равно
, равно ![]() .
.
По условию задачи имеем: ![]() , т.е.
, т.е. ![]() .
.
Преобразовав это уравнение, получим: ![]() .
.
Два комплексных числа равны тогда и только тогда, когда равны соответственно их действительные и мнимые части. Следовательно, последнее уравнение равносильно следующей системе уравнений с действительными переменными x и y:

Возможны два случая:
1) ![]() . Тогда система равносильна системе:
. Тогда система равносильна системе:  , которая
, которая
имеет следующие решения: ![]()
![]() ;
; ![]()
![]() .
.
2) ![]() . Тогда система равносильна системе
. Тогда система равносильна системе  , которая имеет два решения:
, которая имеет два решения: ![]() и
и ![]() .
.
Итак, искомых чисел четыре: ![]() ;
; ![]() ;
; ![]() , из них два числа
, из них два числа ![]() и
и ![]() – действительные, а два других
– действительные, а два других ![]() и
и ![]() – комплексно сопряженные.
– комплексно сопряженные.
Ответ: ![]() ;
; ![]() ;
; ![]() .
.
Задача 21. Известно, что ![]() ,
, ![]() . Найдите:
. Найдите:
а) ![]() ; б)
; б)  .
.
Решение
а)  ,
,
б)  .
.
Ответ: а) ![]() ; б)
; б) ![]() .
.
Задача 22. При каких действительных значениях x и y комплексные числа ![]() и
и ![]() будут сопряженными?
будут сопряженными?
Решение
Комплексные числа ![]() и
и ![]() будут ком-
будут ком-
плексно сопряженными, если выполняются условия:




Ответ: ![]() ;
; ![]() .
.
Задача 23. Докажите тождество ![]() .
.
Решение
Пусть ![]() ,
, ![]() ,
, ![]() . Тогда
. Тогда ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() .
.
Отсюда легко следует доказываемое тождество.
Задача 24. Докажите, что если число ![]() является чисто мнимым, то
является чисто мнимым, то ![]() .
.
Решение
По условию ![]() , где b – действительное число, тогда
, где b – действительное число, тогда ![]() ,
, ![]() ,
,  .
.
Тождество доказано.
Задача 25. Пусть ![]() . Докажите, что
. Докажите, что ![]() .
.
Решение
Поскольку ![]() , то
, то
![]()
![]()
![]()
Тождество доказано.
Задача 26. Решите уравнение ![]() .
.
Решение
Пусть ![]() . Тогда данное уравнение запишется в виде
. Тогда данное уравнение запишется в виде ![]() , откуда
, откуда ![]() . Комплексное число равно нулю, тогда и только тогда, когда его действительная и мнимая части равны нулю; поэтому для нахождения неизвестных x и y получим систему:
. Комплексное число равно нулю, тогда и только тогда, когда его действительная и мнимая части равны нулю; поэтому для нахождения неизвестных x и y получим систему:

Из второго уравнения этой системы находим: x=0 и y=0. При x=0 первое уравнение системы запишется в виде ![]() или
или ![]() . Отсюда находим
. Отсюда находим ![]() или
или ![]() . Таким образом, числа
. Таким образом, числа ![]() ,
, ![]() ,
, ![]() являются решениями данного уравнения.
являются решениями данного уравнения.
При y=0 для нахождения x получаем уравнение ![]() . Отсюда следует, что x=0, и тем самым
. Отсюда следует, что x=0, и тем самым ![]() .
.
Ответ: ![]() ;
; ![]() ;
; ![]() .
.
Задача 27. Решить систему уравнений:

Решение
Полагая ![]() , имеем
, имеем


следовательно,  и
и  .
.
После преобразований данная система принимает вид

Решение полученной системы является пары ![]() и
и ![]() . Таким образом, исходная система имеет два решения
. Таким образом, исходная система имеет два решения ![]() и
и ![]() .
.
Ответ: ![]() ;
; ![]() .
.
Задача 28. Докажите, что если ![]() , то
, то  .
.
Решение
Предположим, что существует такое комплексное число ![]() ,
, ![]() , для которого выполнено неравенство
, для которого выполнено неравенство  . Тогда
. Тогда 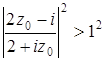 , или
, или ![]() .
.
Поскольку
![]()
![]()
![]()
![]()
![]()
![]()
то ![]() и
и ![]() – действительные числа. Поэтому из последнего неравенства получим неравенство:
– действительные числа. Поэтому из последнего неравенства получим неравенство: ![]() .
.
Следовательно, ![]() .
.
Полученное противоречие доказывает утверждение.
Задача 29. Решите уравнение ![]() .
.
Решение
По формулам корней квадратного уравнения имеем:  .
.
Извлекая корень квадратный из числа ![]() , получаем
, получаем ![]() .
.
Следовательно, ![]() ;
;
![]() .
.
Ответ: ![]() ;
; ![]() .
.
Задача 30. Извлеките квадратный корень из комплексного числа ![]() .
.
Решение
Пусть ![]() , где
, где ![]() .
.
По формуле 


Таким образом ![]() .
.
Ответ: ![]() .
.
Задача 31. Решите уравнение: ![]() .
.
Решение
Имеем ![]() ,
, ![]() ,
, ![]()
![]() .
.
Получаем ![]()
Извлечем квадратный корень из комплексного числа ![]() по формулам:
по формулам:
![]() ;
;  ;
; ![]()
Так как ![]() ,
, ![]() Тогда
Тогда 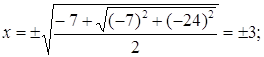


Итак, ![]() , тогда
, тогда ![]()
Где ![]() и
и ![]()
Можно сделать проверку по теореме Виета:
![]() и
и ![]() .
.
Ответ: ![]() ;
; ![]() .
.
Задача 32.
Пусть ![]() ,
, ![]() . При каких действительных значениях a и b выполняется условие
. При каких действительных значениях a и b выполняется условие  ?
?
Решение
Находим

![]() .
.
Используя условие равенства двух комплексных чисел, получаем систему

![]()

Ответ: ![]() .
.
2. 2. Геометрическая интерпретация комплексных чисел
Введем на плоскости прямоугольную систему координат xOy и поставим в соответствии каждому комплексному числу ![]() точку плоскости с координатами (a; b). Полученное соответствие между всеми комплексными числами и всеми точками плоскости взаимно однозначно: каждому комплексному числу
точку плоскости с координатами (a; b). Полученное соответствие между всеми комплексными числами и всеми точками плоскости взаимно однозначно: каждому комплексному числу ![]() соответствует одна точка плоскости с координатами (a; b), и обратно, каждой точке плоскости с координатами (a; b) соответствует единственное комплексное число
соответствует одна точка плоскости с координатами (a; b), и обратно, каждой точке плоскости с координатами (a; b) соответствует единственное комплексное число ![]() (см. рис. 1).
(см. рис. 1).
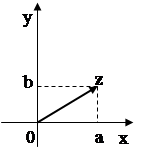
Рис. 1
Таким образом, z одновременно обозначают и комплексное число, и точку, изображающую это комплексное число.
Комплексное число ![]() называется комплексной координатой точки (a; b).
называется комплексной координатой точки (a; b).
Поскольку при указанном соответствии действительные числа ![]() изображаются точками оси абсцисс, то ось Ox называется действительной осью. Ось Oy, на которой лежат чисто мнимые числа
изображаются точками оси абсцисс, то ось Ox называется действительной осью. Ось Oy, на которой лежат чисто мнимые числа ![]() , называется мнимой осью. Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью.
, называется мнимой осью. Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью.
Комплексное число ![]() может также изображаться вектором с координатами a и b, идущим из начала координат в точку (a; b) (см. рис. 1). По определению модуля комплексного числа
может также изображаться вектором с координатами a и b, идущим из начала координат в точку (a; b) (см. рис. 1). По определению модуля комплексного числа
![]() ,
,
модуль комплексного числа равен длине вектора ![]() .
.
Задача 33. Изобразите на комплексной плоскости (рис.2), следующие комплексные числа:
![]()
![]()
![]()
![]()
Решение
Данным комплексным числам соответствуют точки комплексной плоскости.
![]()
![]()
![]()
![]()
Покажем их.

Рис.2
Задача 34. Найдите комплексную координату середины отрезка AB, если комплексные координаты его концов равны ![]() и
и ![]() соответственно.
соответственно.
Решение
Обозначим середину отрезка AB через O1. Тогда
![]() .
.
Учитывая, что комплексная координата вектора равна ![]() , получим
, получим ![]() .
.
Ответ: ![]() .
.
Задача 35. Изобразите графически множество всех точек комплексной плоскости, для которых выполняются данные условия:
а) ![]() , б)
, б) ![]() , в)
, в) ![]() , г)
, г) ![]() , д)
, д) ![]() ,
,
е)  , ж)
, ж) ![]() , з)
, з) ![]() , и)
, и) ![]() , к)
, к) ![]() .
.
Решение
а) ![]() . Из равенств
. Из равенств ![]() и
и ![]() , получаем:
, получаем: ![]() .
.
Множество точек – прямая ![]() (рис. 3).
(рис. 3).
|
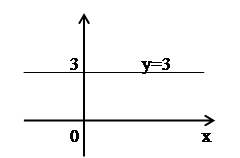
Рис. 3.
б) ![]() .
. ![]() ,
, ![]() . Следовательно,
. Следовательно, ![]() .
.
Множество точек – верхняя относительно оси OX полуплоскость, включая прямую ![]() (рис. 4).
(рис. 4).

Рис. 4.
в) ![]() . Из равенств
. Из равенств ![]() и
и ![]() , получаем:
, получаем: ![]() .
.
Множество точек – прямая ![]() (рис. 5).
(рис. 5).
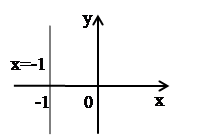
Рис. 5.
г) ![]() ,
, ![]() , и
, и ![]() . Следовательно,
. Следовательно, ![]() .
.
Множество точек – левая относительно прямой ![]() полуплоскость, включая прямую
полуплоскость, включая прямую ![]() (рис. 6).
(рис. 6).

Рис. 6.
д) ![]() .
. ![]() , поэтому
, поэтому ![]() .
.
Множество точек – прямая ![]() . (рис. 7).
. (рис. 7).

Рис. 7.
е) Если ![]() , то условия
, то условия ![]() и
и ![]() означают, что
означают, что ![]() и
и ![]() . Множество точек – часть плоскости, ограниченная снизу прямой
. Множество точек – часть плоскости, ограниченная снизу прямой ![]() , справа
, справа ![]() , исключая указанные прямые (рис. 8).
, исключая указанные прямые (рис. 8).

Рис. 8.
ж) Если ![]() , то
, то ![]() , и условие
, и условие ![]() означает, что
означает, что ![]() , т.е.
, т.е. ![]() . Множество точек – прямая
. Множество точек – прямая ![]() (рис. 9).
(рис. 9).

Рис. 9.
з) Если ![]() , то при условие, что сумма
, то при условие, что сумма ![]() отлична от нуля, имеем
отлична от нуля, имеем  , поэтому
, поэтому  . Следовательно,
. Следовательно, ![]() , откуда получаем уравнение:
, откуда получаем уравнение:
![]() , или
, или ![]() .
.
Преобразуем его
 .
.
Таким образом, множество точек – это окружность с центром в точке O радиуса
радиуса ![]() , у которой «выколота» точка
, у которой «выколота» точка ![]() (рис. 10).
(рис. 10).

Рис. 10.
и) ![]() ; по условию
; по условию ![]() , следовательно,
, следовательно, ![]() .
.
Множество точек – окружность с центром в начале координат ![]() радиуса 1.
радиуса 1.
к) По условию ![]() , поэтому
, поэтому ![]() , т.е.
, т.е. ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Последнее условие означает, что либо
. Последнее условие означает, что либо ![]() , либо
, либо ![]() . В первом случаи получаем уравнение оси Ox, в во втором случаи точку
. В первом случаи получаем уравнение оси Ox, в во втором случаи точку ![]() . Учитывая, что
. Учитывая, что ![]() , т.е. что действительная часть комплексного числа
, т.е. что действительная часть комплексного числа ![]() неотрицательна.
неотрицательна.
Приходим к выводу: искомое множество точек – положительная полуось Ox с началом в точке ![]() .
.
Задача 36. Изобразите на плоскости XOY множество, всех точек ![]() , удовлетворяющих условию:
, удовлетворяющих условию:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) 
Решение
а) ![]() . Для каждого
. Для каждого ![]() число
число ![]() равно расстоянию между точкой
равно расстоянию между точкой ![]() и точкой
и точкой ![]() . Поэтому заданному условию
. Поэтому заданному условию ![]() удовлетворяют те и только те точки, которые лежат на окружности радиуса 1 с центром в точке
удовлетворяют те и только те точки, которые лежат на окружности радиуса 1 с центром в точке ![]() (рис. 11).
(рис. 11).

Рис. 11.
б) ![]() . Для каждого
. Для каждого ![]() число
число ![]() равно расстоянию между точкой
равно расстоянию между точкой ![]() и началом координат. Поэтому условию
и началом координат. Поэтому условию ![]() удовлетворяют те и только те точки, которые лежат внутри кольца, ограниченного двумя концентрическими окружностями с центром в начале координат и радиусами
удовлетворяют те и только те точки, которые лежат внутри кольца, ограниченного двумя концентрическими окружностями с центром в начале координат и радиусами ![]() и
и ![]() соответственно (рис. 12).
соответственно (рис. 12).

Рис. 12.
в) ![]() . Из определения главного аргумента комплексного числа следует, что множество точек z, удовлетворяющих данному соотношению, является открытым лучом Oz (рис 13), образующем угол
. Из определения главного аргумента комплексного числа следует, что множество точек z, удовлетворяющих данному соотношению, является открытым лучом Oz (рис 13), образующем угол ![]() с положительным направлением оси Ох.
с положительным направлением оси Ох.

Рис. 13.
г) ![]() . Пусть
. Пусть ![]() . Тогда данное соотношение перепишется в виде
. Тогда данное соотношение перепишется в виде ![]() или
или ![]() .
.
Отсюда находим: ![]() , т.е.
, т.е. ![]() .
.
Таким образом, ![]() , и, следовательно, исходному соотношению удовлетворяют только те комплексные числа, для которых
, и, следовательно, исходному соотношению удовлетворяют только те комплексные числа, для которых ![]() . Такие точки заполняют всю верхнюю полуплоскость (рис. 14). Этот ответ можно получить из геометрических соображений, учитывая, что ось OX есть перпендикуляр к отрезку, соединяющий точки
. Такие точки заполняют всю верхнюю полуплоскость (рис. 14). Этот ответ можно получить из геометрических соображений, учитывая, что ось OX есть перпендикуляр к отрезку, соединяющий точки ![]() и
и ![]() , восстановленный из его середины.
, восстановленный из его середины.

Рис. 14.
д)  Искомое множество точек есть пересечение кольца, ограниченного окружностями радиусов 1 и 2 с центром в точке
Искомое множество точек есть пересечение кольца, ограниченного окружностями радиусов 1 и 2 с центром в точке ![]() , и второго квадранта (рис. 15).
, и второго квадранта (рис. 15).
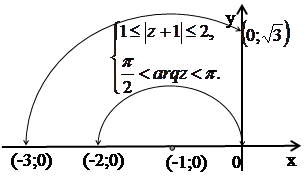
Рис. 15.
Задача 37. Докажите, что расстояние между точками ![]() и
и ![]() равно
равно ![]() .
.
Решение
Так как ![]() , а это и
, а это и
есть, как известно из геометрии, формула расстояния между двумя точками ![]()
![]() и
и ![]()
![]() .
.
Задача 38. Докажите, что если точка ![]() не совпадает с точкой
не совпадает с точкой ![]() , то равенство
, то равенство ![]() задает уравнение прямой, перпендикулярной отрезку, соединяющему точки
задает уравнение прямой, перпендикулярной отрезку, соединяющему точки ![]() и
и ![]() , и проходящей через его середину.
, и проходящей через его середину.
Решение
Все точки ![]() , удовлетворяющие равенству
, удовлетворяющие равенству ![]() , равноудалены от точек
, равноудалены от точек ![]() и
и ![]() и поэтому, как это известно из геометрии, лежат на прямой, перпендикулярной отрезку, соединяющему точки
и поэтому, как это известно из геометрии, лежат на прямой, перпендикулярной отрезку, соединяющему точки ![]() и
и ![]() , и проходящей через его середину. Обратно, все точки
, и проходящей через его середину. Обратно, все точки ![]() этой прямой, очевидно, удовлетворяют равенству
этой прямой, очевидно, удовлетворяют равенству ![]() , следовательно, это равенство является уравнением указанной выше прямой.
, следовательно, это равенство является уравнением указанной выше прямой.
Задача 39. Укажите, где на плоскости расположены точки, соответствующие комплексным числам ![]() , для которых
, для которых ![]() .
.
Решение
Представим выражение ![]() в виде разности двух комплексных чисел:
в виде разности двух комплексных чисел: ![]() . Тогда становится ясно, что равенство
. Тогда становится ясно, что равенство ![]() является уравнением окружности с центром в точке
является уравнением окружности с центром в точке ![]() и радиусом 2.
и радиусом 2.
Неравенству ![]() удовлетворяют внутренние точки указанного круга вместе с точками, лежащими на окружности
удовлетворяют внутренние точки указанного круга вместе с точками, лежащими на окружности ![]() , тогда неравенству
, тогда неравенству ![]() соответствует внешность круга радиуса 1 концентрическому первому.
соответствует внешность круга радиуса 1 концентрическому первому.
Так как нас интересуют точки, удовлетворяющие одновременно двум условиям: ![]() , поэтому искомая область является пересечением двух найденных областей и представляет собой кольцо, содержащее точки внешней ограничивающей окружности. Так как левое неравенство является строгим, точки внутренней ограничивающей окружности не входит в полученную область (рис. 16).
, поэтому искомая область является пересечением двух найденных областей и представляет собой кольцо, содержащее точки внешней ограничивающей окружности. Так как левое неравенство является строгим, точки внутренней ограничивающей окружности не входит в полученную область (рис. 16).

Рис. 16.
Задача 40. Укажите, где на плоскости расположены точки, соответствующие комплексным числам, удовлетворяющим условию: ![]() .
.
Решение
Равенство ![]() является уравнение прямой l, перпендикулярной отрезку AB (A (0;0) и B (0;2)) и проходящей через середину, т.е. прямая l параллельна оси Ox и проходит через точку (0;1). Так как из равенств
является уравнение прямой l, перпендикулярной отрезку AB (A (0;0) и B (0;2)) и проходящей через середину, т.е. прямая l параллельна оси Ox и проходит через точку (0;1). Так как из равенств ![]() ,
, ![]() , следует равенство
, следует равенство ![]() , а значит,
, а значит, ![]() , т.е.
, т.е. ![]() .
.
Поэтому этому равенству удовлетворяют точки полуплоскости, лежащие ниже прямой l не входит в указанную область, так как данное неравенство строгое (рис. 17).

Рис. 17.
Задача 41. Изобразите на плоскости комплексные числа ![]() , удовлетворяющие условию:
, удовлетворяющие условию: ![]() .
.
Решение
 . Следовательно,
. Следовательно, ![]() . Таким образом,
. Таким образом, ![]() ,
, ![]() , то
, то
![]() ,
, ![]() ,
, ![]() .
.
Этим числам соответствуют три точки: A (![]() ), B (
), B (![]() ) и C (
) и C (![]() ). Они расположены на единичной окружности и делят ее на три равные части (рис. 18).
). Они расположены на единичной окружности и делят ее на три равные части (рис. 18).

Рис. 18.
Задача 42. Изобразите на плоскости комплексные числа ![]() , удовлетворяющие условию:
, удовлетворяющие условию:  .
.
Решение
 , значит,
, значит, ![]() и
и ![]() .
.
Получили две точки: B (![]() ) и C (
) и C (![]() ) (рис. 19).
) (рис. 19).

Рис. 19.
Задача 43. Изобразите множество точек комплексной плоскости, удовлетворяющих условию:  .
.
Решение
Данное неравенство равносильно выполнению двух условий: ![]() и
и ![]() . Если
. Если ![]() , где x и y – действительные числа, то получаем следующие неравенства:
, где x и y – действительные числа, то получаем следующие неравенства: 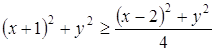 ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Искомая область лежит вне круга с центром в точке (-2; 0) радиуса 2, включая границу круга и исключая точку (2; 0) (рис. 20).
. Искомая область лежит вне круга с центром в точке (-2; 0) радиуса 2, включая границу круга и исключая точку (2; 0) (рис. 20).

Рис. 20.
Задача 44. Изобразите множество точек комплексной плоскости, удовлетворяющих условию:  .
.
Решение
Данное неравенство равносильно выполнению двух условий:
![]() и
и ![]() . Если положить
. Если положить ![]() , то получаем следующие неравенства:
, то получаем следующие неравенства:
![]() .
.
Преобразуем его
![]() ,
,
![]() ,
, ![]() ,
,
Получаем ![]() .
.
Искомая область – круг с центром в точке (0; 2) радиуса 2, включая границу круга и исключая точку (0; 1) (рис. 21).

Рис. 21.
Задача 45. Изобразите множество точек комплексной плоскости, удовлетворяющих условию:  .
.
Решение
Положим ![]() .
.
Тогда  ,
,  .
.
Неравенство  при
при ![]() равносильно неравенству
равносильно неравенству ![]() или
или  . Последнее неравенство задает круг с центром в точке (0; 0,5) и радиусом 0,5 включая границу круга. Вследствие ограничения
. Последнее неравенство задает круг с центром в точке (0; 0,5) и радиусом 0,5 включая границу круга. Вследствие ограничения ![]() точка (0; 0) не принадлежит заданному множеству (рис. 22).
точка (0; 0) не принадлежит заданному множеству (рис. 22).

Рис. 22
Задача 46. Изобразите на комплексной плоскости множество точек, удовлетворяющих неравенствам: ![]() .
.
Решение
Представим число ![]() как
как ![]() . Тогда
. Тогда
![]() ;
;
![]() .
.
По условию, ![]() , откуда
, откуда
![]() ;
; ![]() ;
;
![]() .
.
Левая часть двойного неравенства задает область, лежащую вне круга с центром в точке K(–0,5; 0,5) и радиусом 1. правая часть задает круг с центром в точке K и радиусом 2. В каждом случае граница не включается в заданное множество. Искомое множество точек изображено на рис. 23.

Рис.23.
Задача 47. Из всех чисел ![]() , удовлетворяющих условию
, удовлетворяющих условию ![]() , найдите такие, что
, найдите такие, что ![]() принимает наименьшее значение.
принимает наименьшее значение.
Решение
I способ.
Пусть ![]() . Тогда
. Тогда ![]() .
.
Уравнение ![]() задает на комплексной плоскости окружность с центром в точке O(0; 0) и радиусом 5. С геометрической точки зрения величина
задает на комплексной плоскости окружность с центром в точке O(0; 0) и радиусом 5. С геометрической точки зрения величина ![]() представляет собой сумму расстояний от точки, соответствующей комплексному числу
представляет собой сумму расстояний от точки, соответствующей комплексному числу ![]() , до точек A(7; 0) B(0; 7), соответствующих числами 7 и 7i. Из рис. 24 видно, что окружность с центром в O и радиусом 5 пересекает отрезок AB в двух точках P и Q. Эти точки и будут соответствовать тем комплексным числам, для которых величина
, до точек A(7; 0) B(0; 7), соответствующих числами 7 и 7i. Из рис. 24 видно, что окружность с центром в O и радиусом 5 пересекает отрезок AB в двух точках P и Q. Эти точки и будут соответствовать тем комплексным числам, для которых величина ![]() принимает наименьшее значение.
принимает наименьшее значение.
Действительно, для точек P и Q значение ![]() равно длине отрезка AB, а для любой точки N окружности, отличной от P и Q, в силу неравенства треугольника справедливо соотношение AN+BN>AB.
равно длине отрезка AB, а для любой точки N окружности, отличной от P и Q, в силу неравенства треугольника справедливо соотношение AN+BN>AB.
|

Рис. 24.
Найдем координаты точек P и Q. Эти точки лежат на прямой AB, которая задается уравнением ![]() . Решим систему
. Решим систему

Так как ![]() , то перейдем к системе
, то перейдем к системе

Уравнение ![]() имеет корни 3 и 4, поэтому решениями системы являются пары (3; 4) и (4; 3). Таким образом, точкам P и Q соответствуют числа
имеет корни 3 и 4, поэтому решениями системы являются пары (3; 4) и (4; 3). Таким образом, точкам P и Q соответствуют числа ![]() и
и ![]() .
.
II способ. Пусть ![]() . Тогда
. Тогда ![]() (см. I способ);
(см. I способ);
![]() .
.
![]() Найдем пары (x; y), для которых достигается минимум функции
Найдем пары (x; y), для которых достигается минимум функции ![]() при условии
при условии ![]() . Поскольку функция
. Поскольку функция ![]() принимает не отрицательное значения при всех допустимых x и y, вместо минимума функции φ можно рассматривать минимум функции
принимает не отрицательное значения при всех допустимых x и y, вместо минимума функции φ можно рассматривать минимум функции
![]() .
.
Преобразуем последнее выражение к виду
![]() ,
,
так как ![]() , то
, то ![]() ,
,
откуда ![]() .
.
Произведем замену ![]() и найдем значение t, для которых достигается минимум функции
и найдем значение t, для которых достигается минимум функции ![]() или
или ![]() , или после замены
, или после замены ![]() – те значения p, при которых минимально выражение
– те значения p, при которых минимально выражение ![]() .
.
Исследуем функцию ![]() с помощью производной. Имеем
с помощью производной. Имеем  ;
; ![]() , если
, если ![]() , т.е. если
, т.е. если ![]() , а
, а ![]() . Последнее равенство выполняется при
. Последнее равенство выполняется при ![]() .
.
Нетрудно убедиться в том, что если ![]() , то
, то ![]() , т.е.
, т.е. ![]() убывает, а если
убывает, а если ![]() , то
, то ![]() , т.е.
, т.е. ![]() возрастает. При
возрастает. При ![]() функция
функция ![]() принимает наименьшее значение.
принимает наименьшее значение.
Значению ![]() соответствует
соответствует ![]() , при
, при ![]() . Отсюда, учитывая соотношение
. Отсюда, учитывая соотношение ![]() , находим
, находим ![]() ,
, ![]() или
или ![]() ,
, ![]() и получаем окончательный ответ.
и получаем окончательный ответ.
Ответ: ![]() и
и ![]() .
.
Замечание. Конечно, II способ более трудоемкий, но вместе с тем и более универсальный. В частности, если бы на отрезке AB не нашлось ни одной точки, удовлетворяющей заданному в условии равенству, то решение I способом было бы вообще невозможно.
Задача 48. Изобразите множество точек ![]() комплексной плоскости, удовлетворяющих условию:
комплексной плоскости, удовлетворяющих условию: ![]() .
.
Решение
Представим ![]() в виде
в виде ![]() и преобразуем заданную дробь:
и преобразуем заданную дробь:
 .
.
Мнимая часть дроби равна 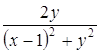 .
.
Неравенство 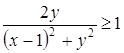 равносильно системе
равносильно системе
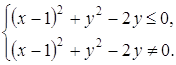
Неравенство ![]() перепишем в виде
перепишем в виде ![]() . Это соотношение задает круг с центром в точке (1; 1) и радиусом 1. Точка (1;0) принадлежит кругу, однако ее координаты не удовлетворяют второму условию системы. Полученное множество изображено на рис. 25.
. Это соотношение задает круг с центром в точке (1; 1) и радиусом 1. Точка (1;0) принадлежит кругу, однако ее координаты не удовлетворяют второму условию системы. Полученное множество изображено на рис. 25.

Рис. 25.
Задача 49. Среди комплексных чисел ![]() , удовлетворяющих условию:
, удовлетворяющих условию: ![]() , найдите число с наименьшим модулем.
, найдите число с наименьшим модулем.
Решение
Воспользуемся геометрическим смыслом модуля комплексного числа. Как известно, для комплексных чисел ![]() и w величина
и w величина ![]() равна расстоянию между точками комплексной плоскости, соответствующими числами
равна расстоянию между точками комплексной плоскости, соответствующими числами ![]() и w. Точки, соответствующие числам
и w. Точки, соответствующие числам ![]() , для которых выполняется равенство
, для которых выполняется равенство ![]() , равноудалены от точек (0; 0) и (0; 2) комплексной плоскости, а, следовательно, образуют прямую
, равноудалены от точек (0; 0) и (0; 2) комплексной плоскости, а, следовательно, образуют прямую ![]() . Среди точек прямой наименее удаленной от начала координат является точка (0; 1). Она соответствует числу
. Среди точек прямой наименее удаленной от начала координат является точка (0; 1). Она соответствует числу ![]() – числу с наименьшим модулем, удовлетворяющему заданному уравнению.
– числу с наименьшим модулем, удовлетворяющему заданному уравнению.
Ответ: ![]() .
.
Задача 50. Пусть M – множество точек ![]() комплексной плоскости таких, что
комплексной плоскости таких, что ![]() ; K – множество точек
; K – множество точек ![]() комплексной плоскости вида
комплексной плоскости вида ![]() , где
, где ![]() . Найдите расстояние между фигурами M и K.
. Найдите расстояние между фигурами M и K.
Решение
I способ.
Пусть ![]() ; тогда
; тогда ![]() , откуда
, откуда
![]() . Множество точек M комплексной плоскости, удовлетворяющих данному условию, есть окружность с центром в точке O1 (0;
. Множество точек M комплексной плоскости, удовлетворяющих данному условию, есть окружность с центром в точке O1 (0; ![]() ) и радиусом 0,5.
) и радиусом 0,5.
По условию, ![]() , т.е.
, т.е. ![]() . Полагая
. Полагая ![]() , имеем
, имеем ![]() и
и ![]() .
.
Множество K точек комплексной плоскости, удовлетворяющих этому условию, есть окружность с центром в точке O2 (–![]() ; 0) и радиусом 0,5. Так как окружности M и K не имеют общих точек, то расстоянием между ними (рис. 26) является длина отрезка PN линии центров, т.е.
; 0) и радиусом 0,5. Так как окружности M и K не имеют общих точек, то расстоянием между ними (рис. 26) является длина отрезка PN линии центров, т.е. ![]() .
.

Рис. 26.
Ответ: 1.
Замечание. Геометрическое обоснование того, что длина отрезка PN есть расстояние между данными фигурами, весьма просто. Действительно, возьмем на окружностях K и M такие точки N1 и P1 соответственно (рис. 27), что ![]() ,
, ![]() . Для ломанной O1P1N1O2 и прямой O1O2 выполняется неравенство O1P1+ P1N1+ N1O2 > O1P+ PN+ NO2. Вычитая из обеих частей неравенства сумму радиусов, получаем P1N1 > PN.
. Для ломанной O1P1N1O2 и прямой O1O2 выполняется неравенство O1P1+ P1N1+ N1O2 > O1P+ PN+ NO2. Вычитая из обеих частей неравенства сумму радиусов, получаем P1N1 > PN.

Рис. 27.
II способ.
Запишем неравенства ![]() . Таким образом,
. Таким образом, ![]() . Это значит, что расстояние от точек фигуры M до точки O1 (0;
. Это значит, что расстояние от точек фигуры M до точки O1 (0; ![]() ) постоянно и равно 0,5. фигура M – окружность с центром в точке O1 и радиусом 0,5. Условие
) постоянно и равно 0,5. фигура M – окружность с центром в точке O1 и радиусом 0,5. Условие ![]() означает, что множество K получено поворотом точек множества M на угол
означает, что множество K получено поворотом точек множества M на угол ![]() вокруг начала координат, т.е. представляет собой окружность с центром в точке O2 (–
вокруг начала координат, т.е. представляет собой окружность с центром в точке O2 (–![]() ; 0) и радиусом 0,5. Дальнейшие рассуждения такие же, как при решении I способом.
; 0) и радиусом 0,5. Дальнейшие рассуждения такие же, как при решении I способом.
Задача 51. Найдите наибольший модуль комплексного числа ![]() , удовлетворяющего условию
, удовлетворяющего условию ![]() .
.
Решение
Так как ![]() , а
, а ![]() . Это круг с центром в точке A (3; 4) и радиусом
. Это круг с центром в точке A (3; 4) и радиусом ![]() .
.
Поскольку OA= 5, ![]() , имеем
, имеем ![]() . Среди точек круга существует точка
. Среди точек круга существует точка ![]() , для которой
, для которой ![]() . Это точка пересечения границы круга и продолжения отрезка OA.
. Это точка пересечения границы круга и продолжения отрезка OA.
Ответ: 6.
Задача 52. Решите систему уравнений

Решение
Так как  , то
, то ![]() . Это множество – серединный перпендикуляр к отрезку AB, где A (0; 2), B (0; 4) – точки, соответствующие числам
. Это множество – серединный перпендикуляр к отрезку AB, где A (0; 2), B (0; 4) – точки, соответствующие числам ![]() и
и ![]() . Уравнение этого перпендикуляра есть
. Уравнение этого перпендикуляра есть ![]() . Из второго уравнения системы имеем
. Из второго уравнения системы имеем ![]() . Пусть
. Пусть ![]() , тогда
, тогда ![]() . Так как
. Так как ![]() для каждой из искомых точек, то
для каждой из искомых точек, то ![]() ;
; ![]() . корнями этого уравнения являются числа 2 и – 4. системе уравнений удовлетворяют 2 числа:
. корнями этого уравнения являются числа 2 и – 4. системе уравнений удовлетворяют 2 числа: ![]() и
и ![]() .
.
Ответ: ![]() ;
; ![]() .
.
Задача 53. Изобразите на комплексной плоскости множество точек, удовлетворяющих условию  .
.
Решение
Пусть ![]() , тогда
, тогда  и, значит,
и, значит,
 ,
,  . Исходное неравенство перепишется так:
. Исходное неравенство перепишется так:  . Последнее неравенство можно заменить системой двух условий:
. Последнее неравенство можно заменить системой двух условий: ![]() и
и ![]() , или
, или ![]() и
и ![]() .
.
Искомое множество изображено на рис. 28. Отметим, что граница множества (прямая ![]() ) принадлежит ему за исключением точки (0; 0).
) принадлежит ему за исключением точки (0; 0).

Рис. 28.
Задача 53. Множество точек комплексной плоскости определяется условие ![]() . В каких пределах изменяется
. В каких пределах изменяется ![]() .
.
Решение
Множество точек, заданное условием ![]() , определяется на комплексной плоскости круг с центром в точке
, определяется на комплексной плоскости круг с центром в точке ![]() и радиусом 1. такой круг в системе координат xOy задается неравенством
и радиусом 1. такой круг в системе координат xOy задается неравенством ![]() .
.
Пусть ![]() , тогда
, тогда ![]() ,
, ![]() ,
, ![]() . Задача сводиться к определению границ, в которых может изменяться соотношение
. Задача сводиться к определению границ, в которых может изменяться соотношение ![]() при условии
при условии ![]() . Вопрос может быть сформулирован так: при каких значениях
. Вопрос может быть сформулирован так: при каких значениях ![]() система
система

имеет хотя бы одно решение?
Последняя система равносильна следующей:
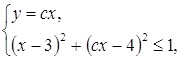 или
или 
Эта система имеет решения тогда, когда имеет решение квадратное неравенство ![]() . Так как коэффициент при
. Так как коэффициент при ![]() положителен, то оно имеет решения, если дискриминант квадратного трехчлена в его левой части неотрицателен. Имеем
положителен, то оно имеет решения, если дискриминант квадратного трехчлена в его левой части неотрицателен. Имеем
![]() .
.
![]() при
при ![]() .
.
Ответ: ![]() .
.
Похожие работы
... учащихся, школьную документацию, сделать выводы о степени усвоения данного понятия. Подвести итог об исследовании особенностей математического мышления и процесса формирования понятия комплексного числа. Описание методов. Диагностические: I этап. Беседа проводилась с учителем математики, которая в 10Є классе преподает алгебру и геометрию. Беседа состоялась по истечении некоторого времени с начала ...
... резонанс" (!)), включающее также оценку собственного поведения. 4. Критическое оценивание своего понимания ситуации (сомнения). 5. Наконец, использование рекомендаций юридической психологии (учет юристом психологических аспектов выполняемых профессиональных действий - профессионально-психологическая подготовленность). Рассмотрим теперь психологический анализ юридических фактов. ...
... математики тригонометрической подстановки и проверка эффективности разработанной методики преподавания. Этапы работы: 1. Разработка факультативного курса на тему: «Применение тригонометрической подстановки для решения алгебраических задач» с учащимися классов с углубленным изучением математики. 2. Проведение разработанного факультативного курса. 3. Проведение диагностирующей контрольной ...
... познавательные задачи призваны лишь дополнить существующие средства обучения и должны находиться в целесообразном сочетании со всеми традиционными средствами и элементами учебного процесса. Отличие учебных задач в преподавании гуманитарных наук от точных, от математических задач состоит лишь в том, что в исторических задачах отсутствуют формулы, жесткие алгоритмы и т.д., что усложняет их решение. ...
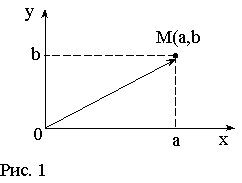

0 комментариев