Метод конформних відображень у теорії фільтрації

3.4.     Метод конформних відображень у теорії фільтрації

Якщо геометрична форма області G складна, то відшукання рішення крайової задачі пов'язане з більшими труднощами. Тому при вирішенні тієї чи іншої крайової задачі намагаються спростити як диференціальне рівняння із граничними умовами, так і вид області, у якій відшукується вирішення. Одним з найпоширеніших методів такого спрощення крайового завдання є метод перетворення незалежних змінних (заміна змінних), зокрема, метод конформного перетворення незалежних змінних.

Нехай у деякій області G необхідно знайти рішення крайової задачі для рівняння Лапласа

. (3.33)

Спробуємо спростити вид області G за допомогою заміни змінних

(3.34)

або

(3.35)

При переході до новим змінних ξ і η міняється не тільки область G, але й саме диференціальне рівняння й граничні умови. Очевидно, найбільший інтерес представляють перетворення, що не міняють вид диференціального рівняння, тобто в нашому випадку перетворення, щодо яких саме рівняння Лапласа залишається інваріантним. Покажемо, що в цьому випадку функції (3.34), що здійснюють перетворення області G у більш просту область D, належать, як і функція (x,y), до класу гармонійних функцій, більше того, вони будуть сполученими гармонійними функціями.

Знайдемо

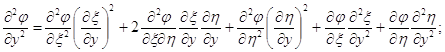
Підставляючи знайдені вирази в рівняння (3.33), одержимо наступне диференціальне рівняння

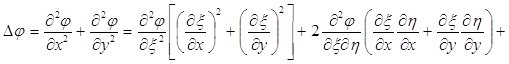
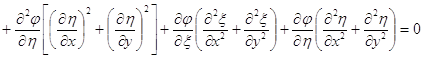. (3.36)

Очевидно, для того, щоб диференціальне рівняння (3.36) було рівнянням Лапласа, необхідно, щоб перетворення (3.34) задовольняло таким вимогам:

(3.37)

(3.38)

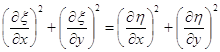. (3.39)

Рівняння (3.37) показують, що функції  і  є гармонійними функціями. Розділивши рівняння (3.38) на , маємо

(3.40)

Підставляючи вираз (3.40) у рівняння (3.39), одержуємо

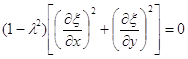,  (3.41)

звідки маємо, що якщо

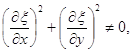 (3.42)

то = ±1 й, отже, з рівнянь (3.40) одержимо або

(3.43)

або

(3.44)

Ці рівняння є умовами Коші-Рімана й показують, що функції  і  є гармонійними функціями. Перетворення, здійснюване такими функціями, переводить нескінченно малі фігури площини хОу в подібні їм фігури площини  за умови, що виконується (3.42). Саме такі перетворення й називаються конформними. Отже, якщо перетворення, здійснюване функціями (3.34), є конформним, то рівняння (3.33) прийме вид

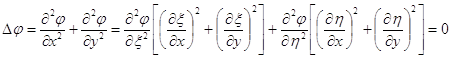
або

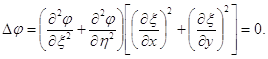
З останньої рівності одержуємо

(3.45)

Отримане рівняння також є рівнянням Лапласа, де частки похідні виражаються через нові незалежні змінні ξ і η - координати області D .

Тепер, якщо утворити комплексну функцію, у якої дійсною й уявною частинами є відповідно функції ξ(x,y) і η(x,y), то така комплексна функція ζ=ξ+iη буде аналітичною функцією комплексної змінної z = x+iy, тобто

ζ(z)=ξ(x,y)+iη(x,y) = f(z). (3.46)

Як ми вже відзначали, перетворення, здійснюване аналітичною функцією (3.47), або, що те ж саме, функціями (3.34), називається конформним усюди в області G , де похідна не дорівнює нулю, тобто де виконується умова

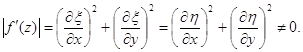(3.47)

Таким чином, рівняння Лапласа є інваріантним щодо перетворень, здійснюваних аналітичними функціями комплексного змінного. Якщо ж перетворення (3.34) здійснюється довільними функціями ξ(x,y) і η(x,y), тобто не є конформним, то рівняння Лапласа (3.33) не переходить у рівняння Лапласа (3.45), а переходить у більше загальне рівняння в частинних похідних другого порядку.

Якщо вдається знайти рішення рівняння Лапласа або якого-небудь іншого рівняння математичної фізики в одній з найпростіших, так званих канонічних областей D (коло, напівплощина, прямокутник, смуга й ін.), тобто якщо визначено функцію  як функція координат ξ і η точок області D , то, скориставшись співвідношеннями (3.47) або (3.34), легко знайти шукане рішення ,  як функцію змінних x й y - координат точок вихідної фізичної області G .

При рішенні конкретних фізичних задач функції  й  мають певну фізичну інтерпретацію. Фізична постановка задач визначає й крайові умови для шуканих функцій. Метод конформних відображень дозволяє також у ряді випадків, а саме, коли граничні умови як для функції (x,y), так і для сполученої з нею функції ψ(x,y), мають спеціальний фізичний зміст, відшукувати рішення рівняння Лапласа безпосередньо. У цих випадках досить знайти аналітичну функцію, конформно фізичну область, що відображає, G на область D зміни фізичних  параметрів (x,y) і ?(x,y) . Вид області D визначається граничними значеннями функцій (x,y) і ψ(x,y).

Для завдань плоскої фільтрації, якщо вдається конформно відобразити область фільтрації z на область комплексного потенціалу ω за допомогою деякої аналітичної функції ω = f(z), те розділивши дійсну й уявну частини функції, що відображає, знайдемо комплексний потенціали фільтрації у вигляді

 (3.48)

де (x, y) - потенціал швидкості фільтрації, а ψ(x, y) - функція струму.

Крім описаної аналітичної функції - комплексного потенціалу фільтрації, у теорії профільної фільтрації розглядаються ще дві аналітичні функції: функція Жуковського G , що визначається рівністю

 (3.49)

і функція Нумерова, обумовлена рівністю

 (3.50)

де ε - кількість води, що надходить у ґрунт (ε > 0) або паркої (ε < 0) з одиниці площі горизонтальної проекції вільної поверхні за одиницю часу.

Таким чином, крайове завдання теорії плоскої сталої або фільтрації, що квазиустано-вились, полягає в тім, щоб для заданої області фільтрації Z знайти одну (або дві) з аналітичних функцій (3.48),(3.49),(3.50).

Похожие работы

Моделювання забруднення ґрунтів

Скачать

35924

3

4

... що концентрація речовини, яка поглинається снігом, пропорційна наземній концентрації. Застосовуючи тепер метод прямих до рівняння (6) для розрахунку забруднення по однорідному профілю, отримаємо рівняння:  (8) 5. Моделювання забруднення ґрунту пестицидами Одним із найбільш важливих інтегральних показників, які відбивають кінцевий результат взаємодії пестицидів, середовища і зовнішніх ...

Вплив на атмосферу підприємств харчової промисловості та шляхи його зниження (на прикладі ВАТ "Жашківський маслозавод")

Скачать

73446

5

6

... параметрів очисного пристрою; проектування та вибір очисного пристрою або фільтра 3.2 Заходи по охороні атмосферного повітря на ВАТ "Жашківський маслозавод" Основними й найбільш дійовими методами боротьби з забрудненням атмосфери на підприємстві є екологічні, діє продумана система заохочувальних і заборонних заходів, які допомагають запобігти забрудненню. Впровадження підприємством певних ...