Навигация
Измеритель рассогласования
4.1 Измеритель рассогласования.
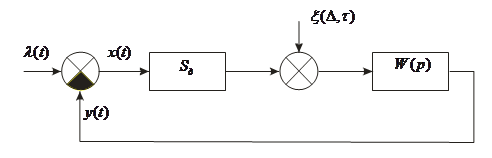
В данной системе используется измеритель рассогласования на сельсинах, схема которого изображена на рисунке 2.
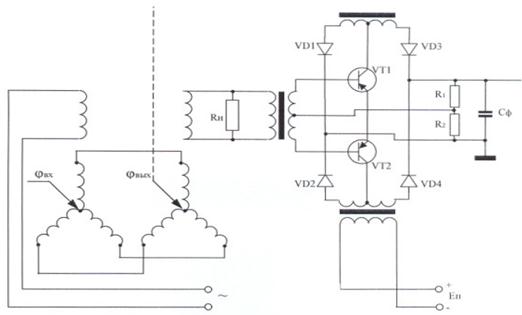
Рис.2. Схема измерителя рассогласования на сельсинах с фазочувствительным усилителем.
Измеритель рассогласования следует считать безынерционным, так как его постоянная времени на несколько порядков меньше постоянных времени остальных звеньев.
![]() ,
, ![]()
![]() ,
,
![]() ,
,
Уравнение измерителя рассогласования:
![]() , (1)
, (1)
где ![]() - коэффициент передачи измерителя рассогласования.
- коэффициент передачи измерителя рассогласования.
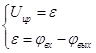 (2)
(2)
Уравнение в переменных состояния и уравнение вход-выход совпадают, так как данный элемент является безынерционным.
Сельсины являются индукционными машинами, которые позволяют при постоянном напряжении на выходе получать на выходных обмотках систему напряжений, амплитуда и фаза которых определяются угловым положением ротора. Сельсины также позволяют преобразовать такую систему напряжений в соответствующее ей угловое положение ротора или в напряжение, фаза и амплитуда которого являются функцией системы входных напряжений и угла поворота ротора. Поэтому сельсины часто применяются в качестве измерителей рассогласования следящих систем.
4.2 Датчик выхода.
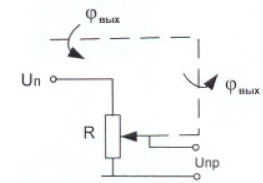
Рис.3. Схема датчика выхода.
Этот датчик угла поворота вала нагрузки описывается уравнением:
![]() , (3)
, (3)
где ![]() .
.
4.3 Усилитель мощности.
Так как по заданию усилитель мощности является звеном первого порядка, то его уравнение имеет вид:
![]() (4)
(4)
это уравнение вход-выход.
Обозначим ![]() , получим следующую систему:
, получим следующую систему:
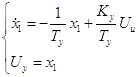 (5)
(5)
это уравнение усилителя.
Передаточная функция усилителя может быть записана в виде:
![]() (6)
(6)
Подставляя исходные значения ![]() ,
, ![]() , получим:
, получим:
![]() (7)
(7)
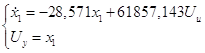 (8)
(8)
![]() (9)
(9)
4.4 Редуктор.
По техническому заданию инерционность редуктора учитывается в уравнении двигателя, поэтому редуктор считается безынерционным звеном и его уравнение имеет вид:
![]()
Уравнение вход-выход и уравнение в переменных состояния:
![]()
Передаточная функция редуктора:
![]()
4.5 Двигатель постоянного тока.
Управление осуществляется по цепи якоря, магнитный поток в зазоре постоянный, а реакция якоря и гистерезис магнитной цепи отсутствует. В этом случае исходные уравнения двигателя оказываются линейными и образуют следующую систему уравнений:
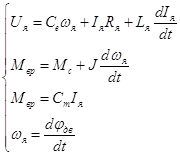 (10)
(10)
Здесь ![]() – приведенный к валу двигателя момент сопротивления;
– приведенный к валу двигателя момент сопротивления;
![]() – приведенный к валу двигателя момент инерции вращающихся частей;
– приведенный к валу двигателя момент инерции вращающихся частей;
![]() – напряжение, приложенное к якорю двигателя;
– напряжение, приложенное к якорю двигателя;
![]() ,
,![]() ,
,![]() ,
,![]() – ток, сопротивление, индуктивность и угловая скорость цепи якоря;
– ток, сопротивление, индуктивность и угловая скорость цепи якоря;
![]() ,
, ![]() – конструктивные постоянные двигателя;
– конструктивные постоянные двигателя;
![]() – угол поворота вала двигателя.
– угол поворота вала двигателя.
Установившийся режим работы двигателя:
Значения переменных в этом режиме будем обозначать с нулевыми индексами:
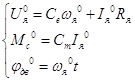 (11)
(11)
Эти уравнения можно использовать для определения коэффициентов ![]() и
и![]() , так как один из установившихся режимов называется номинальным и соответствует значениям:
, так как один из установившихся режимов называется номинальным и соответствует значениям:
![]() ,
, ![]() ,
, ![]() ,
,
![]() (рад/с)
(рад/с)
![]()
![]()
![]()
Модель двигателя необходимо получить в отклонениях от установившегося режима, но поскольку уравнение (10) линейное, то уравнения в отклонениях будут иметь вид (10).
Вывод динамической модели:
Так как индукция якоря учтена в постоянной времени усилителя мощности, то в (10) индукция равна нулю. Отсюда можно найти ток якоря:
![]()
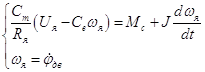 (12)
(12)
Обозначим ![]() ,
, ![]() и получим уравнения в переменных состояния:
и получим уравнения в переменных состояния:
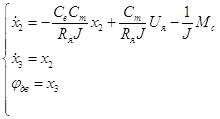 (13)
(13)
Для того, чтобы получить уравнение вход-выход необходимо продифференцировать второе уравнение системы по времени.
![]()
![]() , (14)
, (14)
где ![]() – электромеханическая постоянная двигателя;
– электромеханическая постоянная двигателя;
![]() – электромагнитная постоянная двигателя;
– электромагнитная постоянная двигателя;
![]() ,
, ![]() .
.
Уравнение двигателя принимает вид:
![]() (15)
(15)
Расчет коэффициентов:
![]() (кг·м2)
(кг·м2)
![]()
![]()
![]()
![]() (16)
(16)
Передаточная функция двигателя:
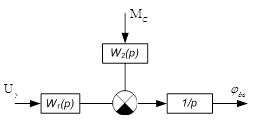
Рис.4.Структурная схема двигателя.
![]() ; (17)
; (17)
![]() .
.
5.ВЫВОД УРАВНЕНИЙ СИСТЕМЫ.
Похожие работы
... в точке подачи обратной связи и определяется как передаточная функция от ошибки x(t) к управляемой величине y(t) . Передаточные функции в обобщенной структурной схеме радиотехнической следящей системы Основная передаточная функция – передаточная функция замкнутой системы. Определяется отношением изображений по Лапласу управляемой величины и задающего воздействия: где Передаточная ...
... где - частотная передаточная функция системы; - спектральная плотность процесса на входе. Преобразовав по Фурье правую и левую часть можно определить корреляционную функцию: . Дисперсия случайного процесса на выходе линейной системы: (1) или: , (2) где Sv(w) –двусторонняя спектральная плотность процесса на выходе системы. При использовании односторонней спектральной плотности ...
... значений относительной нестабильности синхронизируемых генераторов от величины дискрета подстройки по фазе. № п/п 1 3*10-5 2 2*10-4 3 4,8*10-4 4 1,9*10-3 Примеры реализации цифровых следящих систем В качестве примеров рассмотрим схемы цифровых систем ФАПЧ с астатизмом второго порядка, реализующие методы дискретного управления фазой и ...
... переходного процесса для системы с дискретным корректирующим звеном. 2.6.8. Определение рекуррентного уравнения дискретного корректирующего звена. 2.6.9. Разработка принципиальной схемы цифровой следящей системы. 2.7. Расчетно-пояснительная записка должна содержать следующие разделы. 2.7.1. Введение (цель выполнения работы, описание следящей системы, принцип ее ...
0 комментариев