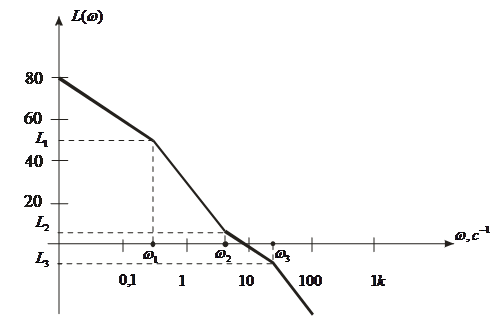
Навигация
Проверка наблюдаемости заданной части системы
6.2 Проверка наблюдаемости заданной части системы.
Для формирования модального управления необходимо измерить переменные состояния системы. Но часто бывает так, что переменные состояния недоступны для прямого измерения с помощью каких-либо датчиков. Обычно измеряются выходные величины объекта (системы), такие, как регулируемые переменные, ошибка системы, положение регулирующего органа, скорость изменения регулируемой величины. Отсюда возникает задача наблюдения, которая состоит в необходимости восстановления значений переменных состояния системы по результатам измерения (наблюдения) некоторых выходных величин системы, а это оказывается возможным только в том случае, если объект (система) является наблюдаемым.
Для определения наблюдаемости системы воспользуемся критерием наблюдаемости, предложенный Калманом. Этот критерий использует матрицу наблюдаемости, которая для систем имеет вид:
 ,
,
где ![]() - размерность вектора переменных состояния.
- размерность вектора переменных состояния.
В нашем случае ![]() , значит:
, значит:
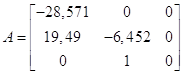 ,
, ![]() ,
,
![]() ,
,
![]()
Матрица N будет иметь вид:
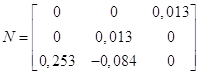
![]()
![]()
Так как ![]() и определитель матрицы N не равен нулю, то объект является вполне наблюдаемым.
и определитель матрицы N не равен нулю, то объект является вполне наблюдаемым.
6.3 Проверка устойчивости нескорректированной системы.
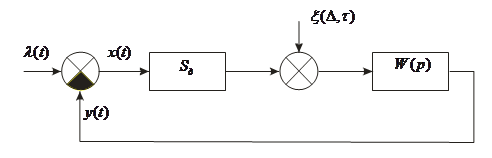
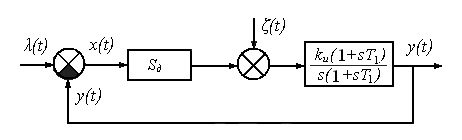
Проверка устойчивости нескорректированной замкнутой системы обычно проводится для того, чтобы убедится, нельзя ли построить требуемую следящую систему лишь на основе заданных элементов. Если выходной сигнал измерителя рассогласования ![]() подать на вход усилителя, то получится замкнутая система, структурная схема которой приведена на рисунке 6.
подать на вход усилителя, то получится замкнутая система, структурная схема которой приведена на рисунке 6.
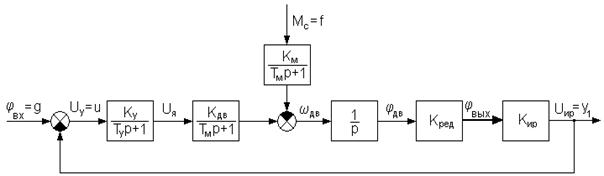
Рис.6.Структурная расчетная схема нескорректированной замкнутой системы.
Для использования алгебраического критерия Гурвица необходимо знать характеристический полином исследуемой замкнутой системы. Таким образом, получим:
![]()
Необходимым, но недостаточным условием устойчивости является положительность всех коэффициентов полинома, но поскольку старшая степень полинома равна трем, то для проверки устойчивости также необходимо воспользоваться частным случаем алгебраического критерия Гурвица – критерием Вышнеградского. Согласно последнему, система будет устойчивой, если будет выполнено условие:
![]() ,
,
где ![]() - коэффициенты характеристического полинома при переменной р в соответствующих степенях.
- коэффициенты характеристического полинома при переменной р в соответствующих степенях.
Подставим коэффициенты нашего характеристического полинома в последнее выражение и проверим выполнение этого условия:
![]()
![]()
![]()
как видно, условие не выполняется.
Следовательно, для заданной замкнутой системы условие не выполняется, то можно сделать вывод о том, что заданная часть системы является неустойчивой.
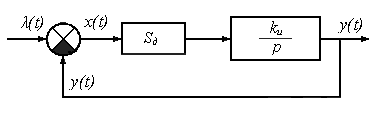
7. СИНТЕЗ УСТРОЙСТВА УПРАВЛЕНИЯ.
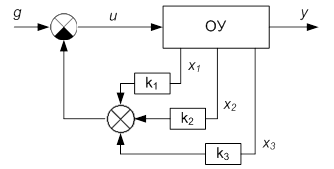
Рис.7. Структурная схема следящей системы.
Допустим, заданная часть системы описывается уравнением:
![]() , (24)
, (24)
где ![]() .
.
Уравнение устройства управления выберем:
![]() (25)
(25)
Здесь ![]() ,
, ![]() и
и ![]() - полиномы, которые нужно определить так, чтобы замкнутая система (24), (25) имела требуемые показатели качества:
- полиномы, которые нужно определить так, чтобы замкнутая система (24), (25) имела требуемые показатели качества:
![]()
![]()
Для вывода расчетных соотношений запишем уравнение замкнутой системы:
![]() (26)
(26)
Чтобы упростить схему управляющего устройства, примем:
![]() ,
,
![]() .
.
При этом передаточная функция замкнутой системы определяется выражением:
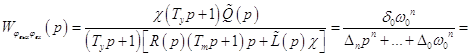
![]()
Число уравнений: ![]()
Число коэффициентов: ![]()
![]() ,
,
![]()
![]() .
.
![]() ,
, ![]()
![]() ,
, ![]()
![]()
Приравнивая числитель и знаменатель, получим:
![]()
![]()
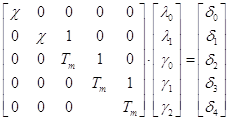
Коэффициенты ![]() выбираются из таблиц нормирующих передаточных функций по
выбираются из таблиц нормирующих передаточных функций по ![]() и
и ![]() . Кроме
. Кроме ![]() из этой таблицы выбирается
из этой таблицы выбирается ![]() :
:
![]() .
.
Подставим численные значения всех коэффициентов и произведем расчет:
![]()
![]()
![]()
![]()
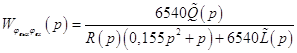
![]()
![]()
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]()
![]()
![]()
![]()
![]()
Искомое уравнение устройства управления имеет вид:
![]()
Похожие работы
... в точке подачи обратной связи и определяется как передаточная функция от ошибки x(t) к управляемой величине y(t) . Передаточные функции в обобщенной структурной схеме радиотехнической следящей системы Основная передаточная функция – передаточная функция замкнутой системы. Определяется отношением изображений по Лапласу управляемой величины и задающего воздействия: где Передаточная ...
... где - частотная передаточная функция системы; - спектральная плотность процесса на входе. Преобразовав по Фурье правую и левую часть можно определить корреляционную функцию: . Дисперсия случайного процесса на выходе линейной системы: (1) или: , (2) где Sv(w) –двусторонняя спектральная плотность процесса на выходе системы. При использовании односторонней спектральной плотности ...
... значений относительной нестабильности синхронизируемых генераторов от величины дискрета подстройки по фазе. № п/п 1 3*10-5 2 2*10-4 3 4,8*10-4 4 1,9*10-3 Примеры реализации цифровых следящих систем В качестве примеров рассмотрим схемы цифровых систем ФАПЧ с астатизмом второго порядка, реализующие методы дискретного управления фазой и ...
... переходного процесса для системы с дискретным корректирующим звеном. 2.6.8. Определение рекуррентного уравнения дискретного корректирующего звена. 2.6.9. Разработка принципиальной схемы цифровой следящей системы. 2.7. Расчетно-пояснительная записка должна содержать следующие разделы. 2.7.1. Введение (цель выполнения работы, описание следящей системы, принцип ее ...
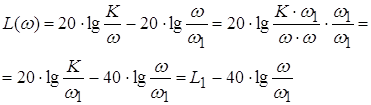
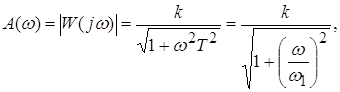
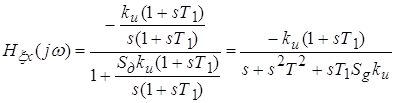
0 комментариев