Математичне моделювання руху поїзда

Вступ

Математична модель в механіці - це замкнута система математичних співвідношень, що дозволяє з прийнятною точністю вивчати особливості поведінки даного об'єкту, що цікавлять дослідника.

Математичне моделювання в механіці керованих систем має ряд особливостей:

·  Що вивчаються в механіці керованого руху об'єкти надзвичайно різноманітні. Автомобіль, гіроскопічний стабілізатор, крокуючий робот, імітатор космічного польоту і т.п. складаються з різних жорстких конструктивних елементів, пристроїв, датчиків, двигунів. З теоретико-механічної точки зору всі ці об'єкти можуть розглядатися як системи, що складаються з великого числа взаємодіючих твердих тіл. Спроба скласти математичну модель такого об'єкту за допомогою класичних методів теоретичної механіки, наприклад у формі рівнянь Лагранжа, зазвичай приводить до неймовірно громіздких рівнянь, що налічують сотні і тисячі доданків. Виникає потреба в наближеному моделюванні, яке для чітко обумовленого класу руху описує потрібні явища з прийнятною точністю.

·  Для систем, керованих рухів, що вивчаються механікою, характерні сильні загасання високочастотних власних складових руху. Наближене моделювання таких систем тяжіє до побудови розкладань А. Пуанкаре і погрансольним методам А.Н. Тихонова - А.Б. Васильєвої.

Проникнення математичних методів в найрізноманітніші, часом несподівані сфери людської діяльності означає можливість користуватися новими, як правило, вельми плідними засобами дослідження. Зростання математичної культури фахівців у відповідних областях призводить до того, що вивчення загальних теоретичних положень і методів обчислень вже не становить серйозних труднощів. Але на практиці виявляється, що одних лише математичних пізнань далеко не достатньо для вирішення того або іншого прикладного завдання необхідно ще отримати навики в перекладі початкового формулювання завдання математичною мовою.

Ситуації моделюють для різних цілей. Головна з них необхідність передбачати нові результати або нові властивості явища. Ці прогнози можуть бути пов'язані з розповсюдженням існуючих результатів або мати принциповіший характер. Часто вони відносяться до умов, які, ймовірно, матимуть місце в деякий момент в майбутньому. З іншого боку, прогнози можуть відноситься до подій, безпосереднє експериментальне дослідження яких нездійсненно. Найбільш важливий приклад такого роду дають численні прогнози, які робилися на основі математичних моделей в програмі космічних досліджень. Проте для цієї мети моделюються не всі ситуації: в деяких випадках досить вміти описувати математичними засобами роботу системи для того, щоб добитися глибшого розуміння явища (саме цю роль і грають багато видатних фізичних теорій, хоча на їх основі робляться також і прогнози). Зазвичай при такому математичному описі не враховується елемент контролю, проте в моделях, побудованих, наприклад, для дослідження роботи мереж, таких як схеми руху потягів або літаків, контроль часто є важливим чинником.

Математична модель є спрощенням реальної ситуації. Відчутне спрощення наступає тоді, коли неістотні особливості ситуації відкидаються і складне початкове завдання зводиться до завдання, що ідеалізується, піддається математичному аналізу. Саме при такому підході в класичній прикладній механіці виникли блоки без тертя, невагомі нерозтяжні нитки, нев'язкі рідини, абсолютно тверді або чорні тіла і інші подібні моделі, що ідеалізуються. Ці поняття не існують в реальній дійсності, вони є абстракціями, складовою частиною ідеалізації, зробленій автором моделі. І проте їх часто можна з успіхом вважати хорошим наближенням до реальних ситуацій. Описаний образ дій при побудові математичних моделей не є єдиним, і цьому зовсім не варто дивуватися. У іншому можливому підході першим кроком є побудова простій моделі декількох найбільш характерних особливостей явища. Це часто робиться для того, щоб відчути дане завдання, причому робиться це ще до того, як саме завдання остаточно сформульоване. Потім ця модель узагальнюється, щоб охопити інші факти, поки не буде знайдено прийнятне або адекватне рішення. Є ще підхід, коли із самого початку вводиться в розгляд одночасне велике число чинників. Він часто застосовується в дослідженні операцій, і такі моделі зазвичай вивчають імітаційними методами з використанням ЕОМ.

Актуальність теми. Одна з основних проблем сучасного локомотивобудування - забезпечення високих тягових і динамічних характеристик локомотивів, які в основному визначаються конструкцією екіпажної частини і технічним станом системи колесо - рейка.

У останні десятиліття з метою зменшення силової взаємодії і зносу гребенів коліс і рейок в кривих велася цілеспрямована і системна робота по впровадженню нових профілів коліс і технологій змазування гребенів і рейок. Це значно понизило гостроту проблеми виходу з експлуатації рейок і бандажів локомотивних коліс внаслідок підвищеного зносу. В той же час збільшилася контактно-втомна пошкоджуваність коліс і рейок.

Дослідження динаміки локомотивів і зношування гребенів в більшості теоретичних і експериментальних робіт виконувалися на вибігу, а не під тягою, при контакті нових коліс, у тому числі і з криволінійним профілем, з новими або мало зношеними рейками і без змазування.

Вивчення динаміки з погляду силової взаємодії і зношування гребенів коліс локомотива в режимах вибігу і тяга при різному технічному стані системи колесо - рейка є актуальним завданням.

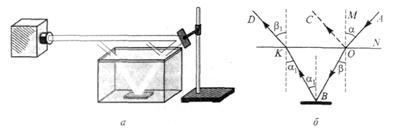
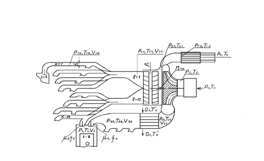
Розділ 1. Опис фізичних явищ, що впливають на рух поїзда

Похожие работы

Психолого-педагогічні аспекти комп’ютерного моделювання при вивченні розділу "Геометричної оптики"

Скачать

135809

1

21

... зичної освіти, а й важливий чинник загального розвитку школяра та професійного становлення у будь-якій галузі. Перша проблема, яку потрібно вирішити, упроваджую чи елементи комп'ютерного моделювання при вивченні фізики – вибір інструментальних засобів його реалізації. У час зародження сучасних інформаційних технологій єдиним способом було використання мов програмування високого рівня. За останні ...

Моделювання робочого процесу чотирьохтактного дизеля

Скачать

99626

0

16

... з системи охолоджування. Манометри показують тиск до і після фільтру, тонкої очистки палива, тобто після підкачуючої помпи і перед насосами високого тиску.   2. МОДЕЛЮВАННЯ РОБОЧОГО ПРОЦЕСУ ЧОТИРЬОХТАКТНОГО ДИЗЕЛЯ Рішення задачі вибору конструктивних і регулювальних параметрів двигунів будь-якого призначення за яким-небудь критерієм може здійснюватися двома методами: експериментальним або ...

Моделювання оптимального розподілу інвестицій за допомогою динамічного програмування

Скачать

48339

9

15

... у формулу (2.11) і визначити наступний стан системи . Для зміненого стану знайти оптимальне управління , підставити у формулу (2.11) і так далі. Для і-гo стану , знайти  і  і т.д. [1]. 3. Оптимальний розподіл інвестицій, як задача динамічного програмування Інвестор виділяє кошти в розмірі  умовних одиниць, котрі повинні бути розподілені між -підприємствами. Кожне і-те підприємство при і ...

Моделювання управління запасами

Скачать

86263

3

4

... прогнозування, визначення економічних і соціологічних тенденцій. Оскільки незалежна потреба величина невизначена, у запас доводиться включати додаткові вироби. 1.2 Моделі систем управління запасами   Система управління запасами реалізує організаційну структуру й поточну політику, що забезпечують підтримку запасу виробів і ефективне керування їм. За допомогою цієї системи здійснюється розробка ...