Навигация
Дослідження напруженого стану плями контакту колеса і рейки
2.2 Дослідження напруженого стану плями контакту колеса і рейки
Взаємодія колеса і рейки є фізичною основою руху рухомого складу по залізницях. Від параметрів цієї взаємодії багато в чому залежать безпека руху і основні техніко-економічні показники господарств шляху і рухомого складу. Так, зокрема, втрати енергії, обумовлені зношуванням в системі колесо-рейка, складають 10% - 30% паливно-енергетичних ресурсів, що витрачаються на тягу. Крім того, витрати на реновацію рейок і колісних пар складають чималу частину загальних витрат дистанцій шляху і локомотивних і вагонних депо відповідно. Особливо великі витрати у зв'язку з цими витратами несуть локомотивні депо, оскільки за останні півстоліття середній термін служби локомотивної колісної пари істотно скоротився.
Серед причин, що викликали в 60-х – 80-х роках минулого сторіччя значне зростання інтенсивності зношування колісних пар, слід зазначити заміну самшитових підшипників ковзання підшипниками кочення, збільшення довжини і маси потягів, звуження колії до 1520 мм, введення профілю рейок (1979г.), що передбачає двоточковий контакт бандажа з головкою рейки та інші. Все це в сукупності призвело до істотної зміни навантаження зони контакту, температури і умов змазування в цій зоні, а також до зміни середньостатистичній швидкості ковзання колеса в поперечному щодо головки рейки напрямі. Результатом цих змін стало істотне зростання інтенсивності зношування коліс рухомого складу, яке, у свою чергу привело до катастрофічних результатів для локомотивного господарства: до кінця дев'яностих років витрати на реновацію колісних пар досягли неприпустимо великих розмірів.
На мал. 1. і 2. представлені графіки заповнення мережі залізниць Росії загартованими рейками [1] і діаграми структури обточувань колісних пар по експлуатаційному парку локомотивів на мережі залізниць Російської Федерації за 1999 і 2002 рр. [2].
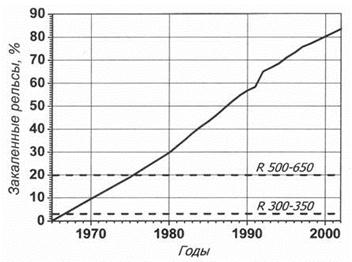
Рис.2 - Заповнення мережі залізниць Росії загартованими рейками
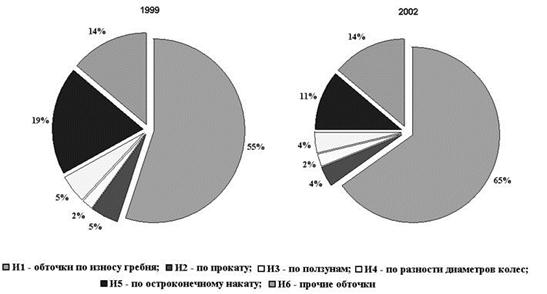
Рис.3 - Структури обточувань колісних пар по експлуатаційному парку
локомотивів на мережі залізниць Російської Федерації за 1999 і 2002 рр.
З порівняльного аналізу діаграм очевидно, що одночасно із зростанням питомої ваги об'ємно загартованих рейок зростає і частка обточувань по зносу гребеня. Така інтенсивність зносу викликала зростання експлуатаційних витрат в локомотивному і вагонному господарствах, пов'язаних з позаплановими обточуваннями колісних пар, додатковим придбанням нових бандажів і коліс.
Відзначимо, що обточування коліс, досягши товщини гребеня мінімального значення, пов'язане із зрізом більшого об'єму металу (так званий технологічний знос) з поверхні катання. Це істотно скорочує термін служби бандажа Рис.4.
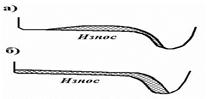
Рис.4- Профіль зносу гребеня:
а – профіль зносу 1960 р., б – профіль зносу 1986 р.
З метою зниження інтенсивності зношування КП до прийнятних значень останніми роками проводиться ряд заходів технічного і організаційно-технологічного характеру [3] (поліпшення конструкції шляху і рухомого складу, вдосконалення геометрії профілю поверхні катання КП і рейок, підвищення якості їх металу і т.д.). На жаль жодне з цих заходів в повному об'ємі проблеми не вирішило.
Кардинальне рішення питання може бути знайдене тільки на базі використання наукових знань в області взаємодії пари колесо-рейка. Необхідне проведення науково обгрунтованої модернізації колісних пар з одночасною розробкою заходів, що забезпечують ефективну експлуатацію і ремонт модернізованих колісних пар.
До технологічних заходів щодо зниження зносу бандажів колісних пар локомотивів відносяться наступні заходи: дослідження процесу взаємодії колеса з рейкою і дія на чинники, що впливають на швидкість зношення бандажа, конструктивні заходи щодо підвищення ресурсу, технологічні методи зміцнення бандажів, зменшення тертя між бандажем і рейкою, контроль і прогнозування технічного стану і ін. (Рис.5.).
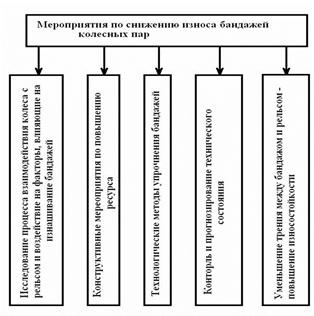
Рис.5- Заходи щодо зниження зношення бандажів колісних пар
На зносостійкість пари “колесо – рейка” за даними [4] впливають: твердість матеріалу бандажів, рейки, вміст вуглецю, структура металів і вміст сірки. Твердість металу є одним з найбільш важливих чинників, які впливають на зношення коліс рухомого складу. Впровадження за останнє десятиліття термічної обробки рейок і додання їм твердості 360 НВ безперечно зіграло важливу роль в поліпшенні роботи залізниць. Проте із зміною твердості рейок заходів по підвищенню твердості бандажів зроблено не було. В результаті відношення твердостей сталі колеса і рейки стало 0,75, це істотно змінило характер зносу в парі “колесо – рейка”. У дослідженнях Вніїжта [4], [5] 1960 – 1990х років наголошувалося, що для рівної зносостійкості відношення твердості колісного зразка до твердості рейкового зразка повинне бути близько 1,2 при прослизанні до 1%, а при прослизанні до 10% – 1,0 – 1,1.
Таким чином, встановлення оптимальної твердості поверхні катання колеса є складним завданням, рішення якого повинне здійснюватися системно з обліком, різних параметрів, а величина твердості поверхні катання коліс на сьогоднішній час обмежена величиною ![]() .
.
Розробка ефективних методів зниження ступеня зносу залежить від наявності методик дослідження, оцінки параметрів контактної взаємодії пари “колесо – рейка” за допомогою чисельних методів.
Завдання контакту кочення двох пружних тіл, що мають однакові характеристики пружності, як для колеса і рейки, може бути представлене роздільно у вигляді нормального і тангенціального завдань. Мета першого завдання полягає у визначенні розміру і форми площадки контакту, а також розподіли нормальної контактної напруги. Результати вирішення нормальної задачі використовуються для знаходження рішення тангенціальною, такою, що полягає в знаходженні розподілу дотичної напруги і моменту в зонах зчеплення і прослизання контактної площадки.
Г. Герц дав перше надійне математичне рішення нормальної задачі. Відстань між недеформованими тілами може бути знайдена геометрично, якщо відомі радіуси кривизни тіл в точці контакту. Пружні властивості колеса і рейки, що описуються коефіцієнтом Пуассона ![]() і модулем пружності, вважаються однаковими. Якщо тіла навантажені нормальною силою, з'являється зона контакту еліптичної форми з великою напіввіссю у напрямі подовжньої осі рейки представленою на Рис.6.
і модулем пружності, вважаються однаковими. Якщо тіла навантажені нормальною силою, з'являється зона контакту еліптичної форми з великою напіввіссю у напрямі подовжньої осі рейки представленою на Рис.6.
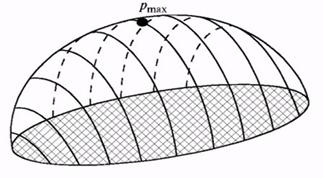
Рис.6 - Розподіл нормальної герцевської напруги на площадці контакту
Максимальна контактна напруга ![]() може бути розрахована по формулі:
може бути розрахована по формулі:
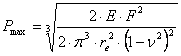 (1)
(1)
де ![]() еквівалентний радіус, залежний від характерних радіусів взаємодіючих тіл (колеса і рейка) в місці контакту.
еквівалентний радіус, залежний від характерних радіусів взаємодіючих тіл (колеса і рейка) в місці контакту.
Таким чином, нормальна напруга на поверхнях катання рейки і колеса залежить від навантаження від колеса на рейку, радіусів поверхонь катання колеса і рейки, властивостей взаємодіючих матеріалів.
Слід мати на увазі, що контактна теорія Герца справедлива при наступних допущеннях:
контактуючі поверхні однорідні і ізотропні;
сили тертя в зоні контакту не діють;
розмір контактної площадки малий в порівнянні з розмірами контактуючих тіл і характерними радіусами кривизни недеформованих поверхонь;
для контактного завдання використано вирішення лінійного пружного напівпростору;
контактуючі поверхні гладкі.
При русі екіпажу положення колісної пари по відношенню до рейок істотно міняється, приводячи до виникнення різних поєднань контактних зон колеса і рейки.
Навіть за умови постійного осьового навантаження нормальна напруга істотно мінятиметься внаслідок відмінності в радіусах кривизни контактуючих поверхонь цих зон.
Якщо в області контакту має місце один радіус кривизни поверхні, можна використовувати рішення Герца. Якщо в області контакту є два або декілька радіусів кривизни, наприклад ![]() і
і ![]() (Рис.7.), рішення Герца несправедливе, і для визначення майданчика контакту слід використовувати негерцівське рішення. Це особливо важливо при різноманітних поєднаннях зношених профілів колеса і рейки.
(Рис.7.), рішення Герца несправедливе, і для визначення майданчика контакту слід використовувати негерцівське рішення. Це особливо важливо при різноманітних поєднаннях зношених профілів колеса і рейки.
При знаходженні нормальної контактної напруги для неконформного негерцівського контакту використовуються різні методи і програми. Зокрема, повне розв’язання негерцевскої задачі може бути знайдене за допомогою програми CONTACT [6]. Проте через те, що вирішення задачі за допомогою цієї програми вимагає великого часу, запропоновані різні варіанти наближеного розв’язання негерцівської задачі. Наприклад, з використанням методу апроксимації негерцівській геометрії еліпсами отримані результати, в достатній мірі що узгоджуються з точним рішенням (Рис.7.) [7].
Інший підхід, що використовується для знаходження контактної напруги між зношеним колесом і рейкою, полягає в моделюванні контактуючих тіл з використанням пружної підстави, при якій деформація поверхонь пропорційна нормальній контактній напрузі [8]. Отримана при цьому максимальна контактна напруга буде в 1,3 більше, ніж при герцівському розв’язанні. Розмір площадки контакту і розподіл нормальної напруги залежать від нормального навантаження, що діє від колеса на рейку, профілів колеса і рейки, поперечного і кутового положення колісної пари на рейках і подуклонки рейок.
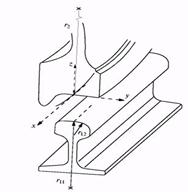
Рис.7 - Геометрія контакту колеса і рейки:
![]() осі системи координат;
осі системи координат; ![]() характерні радіуси (
характерні радіуси (![]() – радіус профілю колеса)
– радіус профілю колеса)
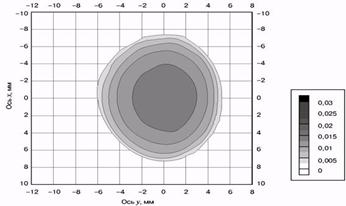
Рис.8 - Форма площадки контакту і розподіл тиску:
![]()
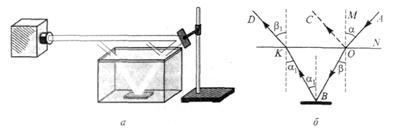
Колісна пара може контактувати з рейкою в двох різних точках [9]. Двоточковий контакт приводить до утворення двох площадок контакту: А на поверхні катання рейки і В на бічній поверхні головки рейки в районі викружки (Рис.9.,а). Внаслідок того що колісна пара при русі в кривій переміщається з деяким кутом набігання а, площадка контакту В зрушена вперед (мал. 8.,б). Збільшення кута набігання приводить до збільшення відстаней між площадками контакту (забігу) і до миттєвої осі обертання колісної пари і тим самим до зростання відносного прослизання і тангенціальної сили, що з ним зв'язана. У зоні того, що стосується гребеня колеса і робочої грані головки зовнішньої рейки рівень розрахункової контактної напруги може досягати 3000 Мпа.
При контакті сильно зношеної рейки з новим або зношеним колесом змінюється форма області розподілу тиску. Розмір площадки контакту істотно зменшується, він зрушується до зовнішньої поверхні зовнішньої рейки, приводячи до збільшення контактного тиску, рівень якого може досягати межі текучості, що викликає пластичну деформацію головки рейки.
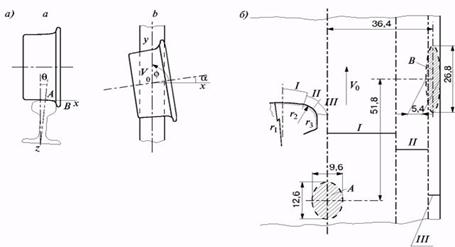
Рис.9 - Положення і розміри контактних майданчиків при двоточковому контакті колеса і рейки ![]() :
:
а) А, В – точки контакту колеса з рейкою; ![]() осі координат
осі координат ![]() кут набігання колеса на рейку;
кут набігання колеса на рейку; ![]() кут подуклонки рейки;
кут подуклонки рейки; ![]() вектор швидкості руху колісної пари б) А, В – майданчики контакту; I, II, III – області контакту;
вектор швидкості руху колісної пари б) А, В – майданчики контакту; I, II, III – області контакту; ![]() радіуси кривизни головки рейки
радіуси кривизни головки рейки
Зазвичай контактна напруга на поверхні катання (область А) колеса вантажного вагону знаходиться в межах 1300 – 1700 Мпа. Збільшення осьового навантаження приводить до зростання контактної напруги пропорційно до її величини (див. формулу 1).
Якщо поверхня катання колеса має прокат з поперечним профілем, що утворився, це призводить до істотного збільшення контактного тиску, який може мати місце по обох сторонах цього профілю. Так, при величині прокату профілю 2 мм розрахункова контактна напруга на обох краях може досягати 6000 Мпа, що свідчить про значний пластичний перебіг матеріалів.
Висока контактна напруга виникає у випадках, якщо профіль колеса своїм зовнішнім краєм спиратиметься на рейку або контактна зона не досягає зовнішнього краю колеса, приводячи до виникнення виступу (фальшивого гребеня) в області зовнішньої частини поверхні катання колеса.
Величина і розподіл контактної напруги істотно залежать від профілів колеса і рейки і від того, який має місце контакт: одноточковий або двоточковий. При конформному профілі розмір площадки контакту збільшується, приводячи до зменшення рівня контактної напруги в порівнянні з неконформними профілями.
Таким чином для оцінки загального напруженого стану в парі колесо-рейка досить вирішити завдання Герца для одноточкового контакту бандажа і рейки. Вирішення задачі проводилося в програмному комплексі ANSYS.
При побудові моделі “колесо – рейка” і проведенні розрахунків розглядався тип рейки Р65 по ГОСТ 18267 – 82, і бандаж ГОСТ 398 – 96, при цьому розглядався незношений профіль бандажа і рейки. Механічні властивості бандажа і рейки, що використовуються для розрахунку представлені в таблиці 1.
Таблиця 1
Механічні властивості бандажа і рейки
| Механічні властивості | Бандаж ГОСТ 398 – 96 | Рейка ГОСТ 18267 – 82 |
| Щільність, кг/м3 | 7850 | 7850 |
| Модуль Юнга, Па |
|
|
| Коефіцієнт Пуассона | 0,3 | 0,3 |
Схема сил, що завантажують колісну пару, представлена на малюнку 9.
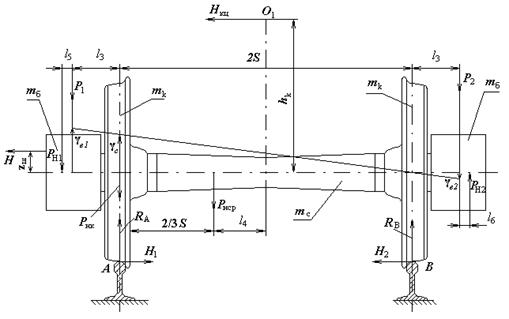
Рис.10. Схема сил, що завантажують колісну пару
У глобальній декартовій системі координат проводилося розбиття колісної пари на тетраедричні кінцеві елементи. Кінцево елементна сітка представлена на Рис11.
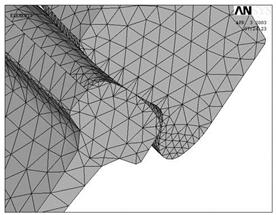
Рис.11. Кінцево елементна модель пари “Колесо - рейка”
На Рис.12 представлена эпюра розподілу напруги в парі “колесо - рейка”.
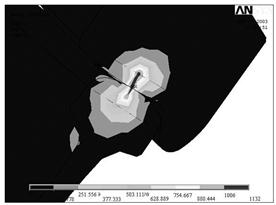
Рис.12. Эпюра розподілу напруги в контакті пари “Колесо - рейка”
При розрахунку було виявлено, що в зоні контакту на поверхні катання колеса напруги досягають значних величин, але вони локалізовані в межах невеликої області. Розмір цієї області порівняємо з розміром плями контакту.
Похожие работы
... зичної освіти, а й важливий чинник загального розвитку школяра та професійного становлення у будь-якій галузі. Перша проблема, яку потрібно вирішити, упроваджую чи елементи комп'ютерного моделювання при вивченні фізики – вибір інструментальних засобів його реалізації. У час зародження сучасних інформаційних технологій єдиним способом було використання мов програмування високого рівня. За останні ...
... з системи охолоджування. Манометри показують тиск до і після фільтру, тонкої очистки палива, тобто після підкачуючої помпи і перед насосами високого тиску. 2. МОДЕЛЮВАННЯ РОБОЧОГО ПРОЦЕСУ ЧОТИРЬОХТАКТНОГО ДИЗЕЛЯ Рішення задачі вибору конструктивних і регулювальних параметрів двигунів будь-якого призначення за яким-небудь критерієм може здійснюватися двома методами: експериментальним або ...
... у формулу (2.11) і визначити наступний стан системи . Для зміненого стану знайти оптимальне управління , підставити у формулу (2.11) і так далі. Для і-гo стану , знайти і і т.д. [1]. 3. Оптимальний розподіл інвестицій, як задача динамічного програмування Інвестор виділяє кошти в розмірі умовних одиниць, котрі повинні бути розподілені між -підприємствами. Кожне і-те підприємство при і ...
... прогнозування, визначення економічних і соціологічних тенденцій. Оскільки незалежна потреба величина невизначена, у запас доводиться включати додаткові вироби. 1.2 Моделі систем управління запасами Система управління запасами реалізує організаційну структуру й поточну політику, що забезпечують підтримку запасу виробів і ефективне керування їм. За допомогою цієї системи здійснюється розробка ...


0 комментариев