Энергия обменного взаимодействия

1.3 Энергия обменного взаимодействия

Для того, чтобы легче перейти к сложным системам, рассмотрим сначала простой случай двух атомов водорода. Каждый из которых состоит из протона и электрона, которые обладают электрическими зарядами +е и –е и магнитными моментами μ и μ (здесь мы не будем обращать внимания, что у электрона и особенно у протона фактические магнитные моменты отличаются от магнетонов Бора). Магнитный момент электрона почти в две тысячи раз больше магнитного момента протона. Пока атомы далеки друг от друга, их взаимодействием можно пренебречь. При их сближении кулоновские силы притяжения и отталкивания между электронами и протонами обоих атомов будут расти обратно пропорционально квадрату расстояния. Но кроме квазиклассической части этих взаимодействий возникнут еще специфические квантовые добавки тоже электростатического происхождения, неизвестные в классической физике.

Дело в том, что электрон в одном атоме физически полностью тождествен с электроном в другом атоме, т.е. мы имеем дело с системой двух тождественных частиц, которые принципиально нельзя пронумеровать.

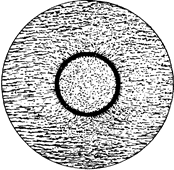
Когда атомы настолько сближены, что образуется молекула водорода Н2 (рисунок 2), то электроны как бы обобществляются на молекулярной орбите и проследить за каждым из них индивидуально нельзя. Они непрерывно обмениваются местами около обоих протонов. С этим обменом тождественных электронов и связано добавочное к обычному квазиклассическому кулоновскому взаимодействию электрическое взаимодействие, называемое обменным. По величине оно близко к квазиклассическому электростатическому взаимодействию, т.е. к 10-13 эрг в расчете на один электрон. Вот это взаимодействие и играет первостепенную роль как в формировании ковалентной химической связи двухатомных – более сложных молекул (в которых мы имеем долю не с простой электростатической связью противоположно заряженных ионов), так и в энергии связи в построенных из нейтральных атомов конденсированных телах (жидкостях и кристаллах). Этот же тип взаимодействия определяет также и атомную упорядоченную магнитную структуру в твердых телах.

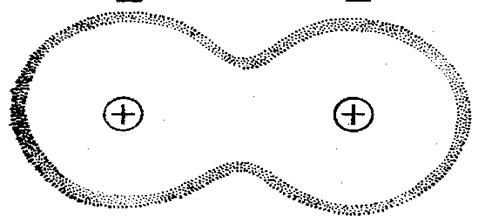
Рисунок 2 - Образованная валентными электронами двух атомов коллективная электронная оболочка молекулы, свойства которой и определяют магнетизм молекулы, качественно отличающиеся от магнетизма исходных атомов.

Как показали квантовомеханические расчеты энергий стационарных состояний двухэлектронных оболочек молекулы водорода или также двухэлектронной оболочки атома гелия, добавочная энергия – энергия обменного взаимодействия U электрического происхождения равна произведению постоянной А1 (которую принято называть обменным интегралом) на скалярное произведение векторов спинов или связанных с ними магнитных моментов μ 1 и μ 2:

U = А1 (μ 1 μ 2) (5)

В частном случае двухэлектронных оболочек молекулы водорода или атома гелия μ 1 и μ 2 – это единые векторы, направленные вдоль спиновых магнитных моментов электронов оболочек, которые могут быть только либо параллельны, либо антипараллельны. В первом случае их скалярное произведение

(μ 1 μ 2) = μ 1 μ 2 соs 00 = 1 (6)

а во втором

(μ 1 μ 2) = μ 1 μ 2 соs 1800 = -1 (7)

Поэтому если обменный интеграл положителен (А>0), то энергия обменного взаимодействия U минимальна и ей соответствует параллельная ориентация спиновых моментов. Действительно из формулы (5) мы получаем тогда:

U = -А (8)

При антипараллельных спинах и при А>0 из формулы (5) находим:

U = А (9)

Т.е. максимальное значение обменной энергии, соответствует неустойчивому состоянию электронной системы молекулы или атома.

Напротив, если обменный интеграл отрицательный (А<0), то минимуму обменной энергии отвечает антипараллельность спиновых моментов:

U = -(-А) * (-1) = -А (10)

а максимуму – их параллельная ориентация::

U =-(-А) * (1) = А (11)

В случае молекулы водорода или атома гелия спиновые моменты антипараллельны (А<0), суммарный магнитный момент равен нулю, поэтому электронные оболочки здесь магнитно-нейтральны. Напротив, в случае, например, молекулы кислорода О2 спины электронов в основном состоянии с минимальной энергией параллельны (А>0) и мы имеем дело в с парамагнитной атомной системой. Обменное взаимодействие быстро убывает с расстоянием. Поэтому когда от двух атомов переходим ко многим (например, в кристалле), основной вклад в обменную связь вносят обменные силы между ближайшими соседними электронами. Тем не менее нельзя пренебрегать и влиянием всех остальных атомов данного тела, поэтому вычисление энергии обменного взаимодействия в твердых телах вызывает затруднение.

Похожие работы

Электричество и магнетизм

Скачать

189451

18

0

... проводимости, запрещенная валентная зона, энергия активации). 8.  Температурная зависимость полупроводников. Литература, рекомендуемая к лабораторной работе:   10.  Матвеев А.Н. Электричество и магнетизм.- М.: Высшая школа, 1983. 11.  Калашников С.Г. Электричество. – М.: Наука, 1977. 12.  Савельев И.В. Курс общей физики. Т.2, Т. 3. – М.: Наука, 1977. 13.  Телеснин Р.В., Яковлев В.Ф. Курс ...

Ферромагнетики

Скачать

42038

10

10

... , что элементарными носителями магнетизма в них являются спиновые магнитные моменты электронов . В современной квантово-механической теории ферромагнетизма объяснена природа самопроизвольной намагниченности ферромагнетиков и природа возникновения сильного внутреннего поля . Ферромагнитными свойствами могут обладать кристаллы веществ, атомы которых имеют не заполненные электронами внутренние ...

Машинная память

Скачать

97096

0

5

... беспредельной ёмкостью памяти, а спецификой механизмов, предохраняющих человеческую память от "переполнения". По быстродействию (скорости записи и воспроизведения информации) машинная память значительно превосходит память человека. Скорость срабатывания элементов, на основе которых строятся современные ЗУ, определяется в конечном счете скоростью протекания электронных процессов, в то время как ...

Исследование магнитного гистерезиса

Скачать

45620

11

15

... включать режим I при входном напряжении частотой 50 Гц, т.е. в "сеть" ибо это действие может привести к порче оборудования. При исследовании явления магнитного гистерезиса производится расчеты напряженности магнитного поля и магнитной индукции по выше рассмотренным формулам. Исследование ферромагнитных свойств электротехнической стали. В качестве исследуемого образца был взят ...