Магнитная анизотропия

1.10 Магнитная анизотропия

В ферромагнитном кристалле имеются взаимодействия, которые ориентируют вектор намагниченности вдоль определенных кристаллографических направлений, называемых осями легкого намагничивания.

Энергия, связанная с этими взаимодействиями, называется энергией магнитной кристаллографической анизотропии или просто энергией магнитной анизотропии.

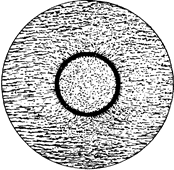
Одна из причин магнитной анизотропии иллюстрируется схемой на рисунке 19. Намагниченность кристалла «чувствует» кристаллическую решетку благодаря перекрытию электронных орбит: спиновые моменты взаимодействуют с орбитальными из-за наличия спин-орбитальной связи, а орбитальные моменты в свою очередь взаимодействуют с кристаллической решеткой за счет существующих в ней электростатических полей и перекрытия волновых функций соседних атомов решетки [8, с. 581-582].

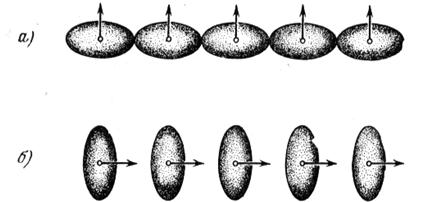
Рисунок 19.

Все известные в настоящее время ферромагнетики – тела кристаллические. Кристаллики очень малы. Но если хорошо отполированную поверхность протравить кислотой и исследовать под микроскопом, то мы увидим различные по форме и величине зерна. Тщательное изучение показывает, что эти отдельные зерна представляют собой кристаллы с неправильными поверхностными границами.

Неправильность границ объясняется тем, что при кристаллизации вещества одновременно начинает расти большое количество кристаллов и они мешают друг другу принять правильные граничные очертания.

Кристаллы, граничная поверхность которых не представляет собой правильной, характерной для кристаллов формы, называются кристаллитами. В кристаллических телах атомы расположены в строго определенном порядке и составляют так называемую кристаллическую решетку. Кристаллические решетки могут быть разнообразными (примеры на рисунке 20).

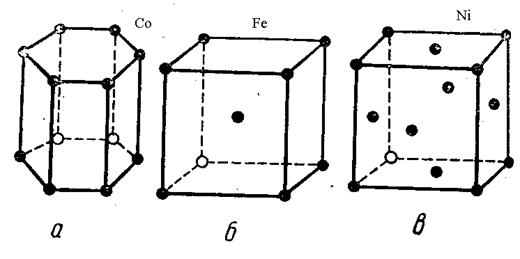
Рисунок 20 - Элементарные ячейки кристаллических решёток: а) гексагональная; б) объёмноцентрированная; в) гранецентрированная.

Асимметрия перекрытия электронных оболочек соседних ионов как одна причин кристаллографической магнитной анизотропии. Вследствие спин-орбитального взаимодействия распределение электронного заряда – не сферическое. Асимметрия связана с направлением спина, поскольку изменение направления спина по отношению к осям кристалла изменяет обменную энергию, а также электростатическую энергию взаимодействия распределений заряда пар атомов. Именно эти эффекты приводят к появлению энергии анизотропии. Энергия системы а иная, чем энергия системы б.

Для кристаллов характерна анизотропность физических свойств. Это значит, что в кристаллах по различным направлениям свойства различны. В телах же не кристаллических (аморфных) все физические свойства по различным направлениям совершенно одинаковы.

Поскольку все ферромагнетики – тела кристаллические, а последним свойственна анизотропия различных физических свойств, то возникает вопрос: являются ли магнитные свойства ферромагнетиков изотропными или анизотропными, т.е. существует ли анизотропия магнитный свойств и если существует, то каких именно?

1) Естественно прежде всего выяснить, как зависит величина спонтанной намагниченности от ее направления в кристалле. Нам уже известно, что величина спонтанной намагниченности равна намагниченности насыщения. Значит, измеряя в кристалле намагниченность насыщения по разным направлениям, мы будем получать значения спонтанной намагниченности по этим направлениям.

Оказалось, что величина спонтанной намагниченности по всем направлениям в кристалле совершенно одинакова. Это справедливо для всех ферромагнитных кристаллов. Для всех ферромагнитных кристаллов характерна изотропия спонтанной намагниченности.

2) Можно исследовать зависимость точки Кюри от направления намагниченности в кристалле, т.е. установить, по всем ли направлениям в кристалле при одной и той же температуре исчезают ферромагнитные свойства.

Оказывается, что и точка Кюри ферромагнетика для всех направлений в кристалле совершенно одинакова. Ферромагнитные свойства теряются в ферромагнетике по всем направлениям при одной и той же температуре. Изотропность точки Кюри объясняется изотропностью спонтанной намагниченности.

Если снимать кривые намагничивания по различным направлениям в ферромагнитных кристаллах (например, для железа), то скажется следующее. Намагниченность монокристалла железа в направлении ребра –куба резко возрастает уже в слабых полях и быстро достигает насыщения (рисунок 21).

вдоль ребра куба (направление [100])

вдоль диагонали грани (направление [110])

вдоль пространственной диагонали (направление [111]).

Рисунок 21 - Кривые намагничивания монокристалла железа по различным кристаллографическим направлениям

При намагничивании вдоль диагонали грани кривая намагничивания сначала резко идет вверх, как и при намагничивании в направлении ребра куба, затем при достижении приблизительно 0,7 от величины насыщения рост намагниченности замедляется и на кривой намагничивания появляется излом. При дальнейшем возрастании поля намагниченность увеличивается. Насыщение намагниченности наблюдается в довольно сильных полях, причем ее величина равна насыщению, полученному при намагничивании вдоль ребра куба (см. рисунок 21, кривая 2). На том же рисунке видно, что при намагничивании вдоль пространственной диагонали быстрый рост намагниченности прекращается, когда она достигает примерно 0,58 от насыщения. Кривая намагничивания в этом месте претерпевает излом, затем следует медленное возрастание намагниченности с ростом поля, пока не будет достигнуто насыщение (кривая 3, рисунок 21).

Таким образом, намагничивание монокристалла железа по различным направлениям происходит по-разному, т.е. в ферромагнитных кристаллах существует магнитная анизотропия.

Магнитную анизотропию удобнее всего характеризовать работой намагничивания. В самом деле, при намагничивании ферромагнетика расходуется некоторое количество энергии, численно определяемое площадью, ограниченной осью намагниченности, кривой намагничивания и продолжением прямой, соответствующей насыщению, до пересечения с осью намагниченности (рисунок 22).

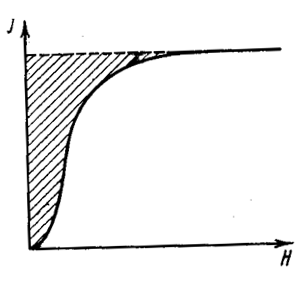
Рисунок 22. Заштрихованная площадь численно равна работе намагничивания.

Из рисунка 21 следует, что работа намагничивания вдоль направления ребра куба для железа наименьшая, вдоль пространственной диагонали – наибольшая, а при намагничивании вдоль диагонали грани она имеет некоторое среднее значение.

Поэтому направление вдоль ребра куба в железе называют направлением легкого намагничивания, а направление, совпадающее с направлением пространственной диагонали, направлением трудного намагничивания.

Исследования, проведенные на монокристаллах никеля, дают прямо противоположную картину. Здесь наибольшая работа при намагничивании затрачивается вдоль ребра куба, которое является направлением трудного намагничивания (рисунок 23, кривая 1). Направлением легкого намагничивания является направление пространственной диагонали (рисунок 23, кривая 3). На рисунке 2 кривая 2 соответствует намагничиванию монокристалла никеля по диагонали грани.

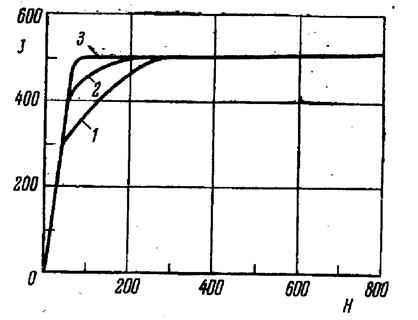
1-вдоль ребра куба;

2-вдоль диагонали грани;

3-вдоль пространственной диагонали.

Рисунок 23 - Кривые намагничевания монокристалла никеля вдоль различных кристаллографических направлений

Монокристалл кобальта имеет всего одну ось легкого намагничивания, совпадающую с направлением гексагональной оси (рисунок 24). На рисунке 25 изображены кривые намагничивания монокристалла кобальта в направлении гексагональной оси (1) и перпендикулярно к ней (2). Таким образом, в железе имеются три оси (6 направлений по оси и против нее) легкого намагничивания и 4 оси (8 направлений) трудного намагничивания; в никеле – 4 оси (8 направлений) легкого намагничивания, 3 оси (6 направлений) трудного намагничивания; в кобальте – 1 ось (2 направления) легкого намагничивания и бесконечное число направлений трудного намагничивания, перпендикулярных гексагональной оси.

.

Рисунок 24. Направление лёгкого намагничивания в монокристалле кобальта совпадает с гексагональной осью.

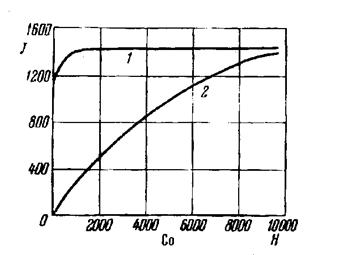Рисунок 25 - Кривые намагничивания монокристалла кобальта: 1– вдоль гексагональной оси; 2 – перпендикулярно гексагональной оси (в базисной плоскости).

Согласно закону сохранения энергии, работа, затраченная на намагничивание ферромагнетика, не может исчезнуть, она превращается в потенциальную энергию намагниченного тела.

Всякое тело, предоставленное самому себе, стремится занять положение, соответствующее минимуму его потенциальной энергии. В соответствии с этим принципом железный стержень в магнитном поле своей осью установится вдоль поля, так как намагничивание вдоль оси стержня требует меньшей энергии, чем намагничивание поперек стержня.

Вырежем шар из монокристалла железа или никеля и поместим его в магнитное поле, предоставив ему возможность любым образом ориентироваться в пространстве. Последнее можно осуществить, например, при помощи подвеса Кардана (рисунок 26).

Рисунок 26 - Шар в подвесе Кардана.

Так как работа намагничивания по различным направлениям в кристалле различна, то шар будет вести себя в магнитном поле, как магнитная стрелка, устанавливаясь вдоль поля одной из своих осей легкого намагничивания. На рисунке 27 изображен шар из монокристалла никеля, на котором точками отмечены выходы осей легкого намагничивания. Таких осей четыре.

Рисунок 27 - Шар из монокристалла никеля. Точками отмечены выходы на поверхность осей лёгкого намагничивания.

Представим себе теперь, что мы ориентировали шар из монокристалла железа в направлении грани куба по отношению к полю. Кристалл намагнитится, и так как намагничивание происходит в направление оси легкого намагничивания, работа намагничивания будет минимальной.

Если теперь поворачивать этот кристалл в магнитном поле, то намагничивание уже не будет совпадать с направлением легкого намагничивания в кристалле, и работа намагничивания будет возрастать. Представим себе, что кристалл ориентирован так, что вектор напряженности магнитного поля лежит в кристаллической решетке в плоскости грани куба. Тогда с изменением угла поворота кристалла относительно поля работа намагничивания будет периодически то возрастать, то уменьшаться.

Пусть работа намагничивания в направлении ребра куба равна U0. Изобразим эту величину в виде отрезка, который численно равен U0. При повороте кристалла на некоторый угол a величина энергии изменится. Пусть она будет равна Ua. Отложим под углом a к отрезку, изображающему U0, отрезок, равный Ua. Если определить значения Ua для различных углов и откладывать под этими углами отрезки, равные значениям энергии, затрачиваемой при намагничивании шара под соответствующим углом, то получим график энергии намагничивания по различным направлениям в плоскости грани куба, или, как говорят, энергетическую диаграмму в этой плоскости (рисунок 28). Как уже отмечалось, различные значения работы намагничивания по различным направлениям в кристалле и характеризуют собой магнитную анизотропию. Численно магнитная анизотропия равна учетверенной разности работ намагничивания в направлении ребра куба и в направлении диагонали грани (рисунок 28).

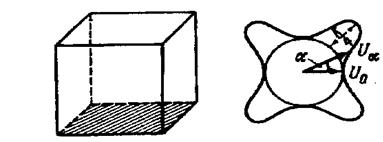
Рисунок 28 - Энергетическая диаграмма в плоскости грани куба монокристалла железа.

Эта величина, отнесенная к единице объема, представляет собой важную характеристику ферромагнетика и называется константой магнитной анизотропии.

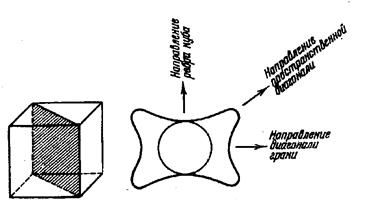
Рисунок 29 - Энергетическая диаграмма монокристалла железа для диагональной плоскости.

На рисунке 29 представлена энергетическая диаграмма в диагональной плоскости кубической решетки. Как видно из рисунка, «горб» соответствует направлению трудного намагничивания, а наиболее глубокие лунки соответствуют направлениям легкого намагничивания.

Изучение энергетической анизотропии кристаллов позволило Н.С. Акулову рассчитать кривые намагничивания монокристаллов по различным направлениям. Рассчитанные кривые оказались в хорошем согласии с опытом.

Для кристаллов кубической системы, энергия, связанная с анизотропией:

U = U0 + K (s12s22 + s22s32 + s12s32 ) (25)

где U0 – энергия в направлении ребра куба кристалла, которое обозначают [100] (рисунок 30);

s1, s2, s3 – косинусы углов между направлениями X, Y, Z и вектором спонтанной намагниченности Js (рисунок 31). При комнатной температуре константа магнитной анизотропии К для железа равна +4,28·105 эрг/см3, а для никеля – 5,12·104 эрг/см3.

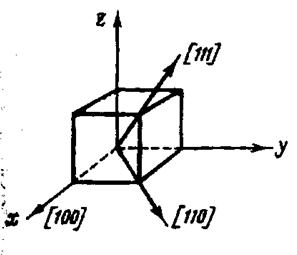
Рисунок 30 - Главные кристаллографические направления в кубическом кристалле.

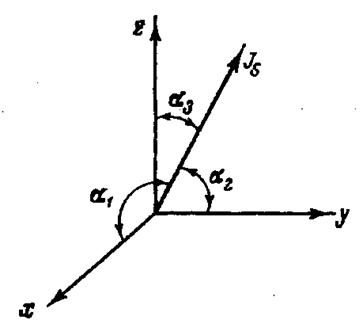
Рисунок 31. S=cos ; S=cos ; S=cos ;

Константа магнитной анизотропии меняется с изменением температуры. На рисунке 32 представлены графики зависимости констант магнитной анизотропии железа и никеля от температуры. Обращает на себя внимание резкая зависимость от температуры константы анизотропии никеля. Даже в области комнатных температур ее величина изменяется в полтора раза.

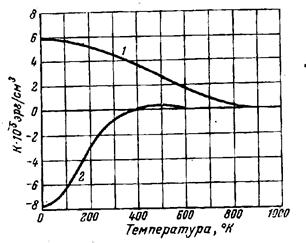
Рисунок 32 - Температурная зависимость констант магнитной анизотропии 1- для железа; 2- для никеля;

Энергия анизотропии для гексагональных кристаллов типа кобальта выражается формулой:

U = U0 + K1 sin2a + K2 sin4a (26)

где К1 и К2 – первая и вторая константы анизотропии;

a - угол между гексагональной осью и направлением вектора спонтанной намагниченности (рисунок 33).[7, с. 65-74]

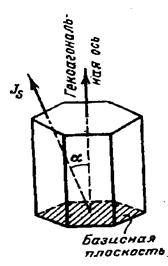
Рисунок 33.