Краткие сведения и задачи по курсу векторной и линейной алгебры

Контрольная работа

Краткие сведения и задачи по курсу векторной и линейной алгебры

Векторная алгебра

Вариант №21

1.         Найти скалярное произведение .

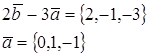
2.         При каком значении α векторы и ортогональны?

;;;

;;;

Два вектора ортогональны, когда их скалярное произведение равно нулю.

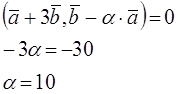
3.         Для прямой М₁М₂ написать уравнение с угловым коэффициентом, в отрезках и общее уравнение. Начертить график прямой. М₁(0,-3) М₂(2,1).

Общий вид уравнения прямой с угловым коэффициентом записывается в виде:

y-y₁=k(x-x₁),

значит для прямой М₁М₂

у+3=kx

Общий вид уравнения прямой, проходящей через две точки записывается в виде:

,

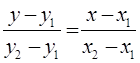значит для прямой М₁М₂

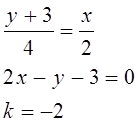
Общий вид уравнения прямой в отрезках записывается в виде:

,

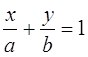Здесь

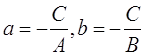
Уравнения прямой в отрезках для прямой М₁М₂

;

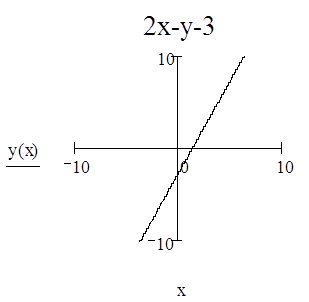
4.   В треугольнике М₀М₁М₂ найти уравнение медианы, высоты, проведенных их вершины М₀, а также уравнение средней линии EF, параллельной основанию М₁М₂.(М₀(-1,-2); М₁(0,-3); М₂(2,1)).

Найдём координаты точки М₃, координаты середины стороны М₁М₂:

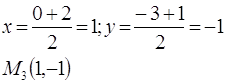
уравнения прямой, проходящей через две точки записывается в виде:

,

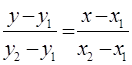уравнение для высоты М₀М₃:

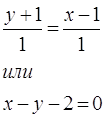
Найдём уравнение прямой М₁М₂:

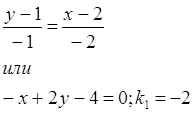
Из условия перпендикулярности (k₂=-1/k₁) следует, что k₂=1/2.

Уравнения прямой с угловым коэффициентом записывается в виде:

y-y₁=k(x-x₁),

тогда уравнение для высоты примет вид:

y+1= (x+2)/2

или

x+2y=0.

Расстояние от точки М(x₀,y₀) до прямой Ax+By+c=0 находится по формуле:

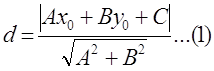
Чтобы найти длину высоту, найдём расстояние от точки М₀(-3,-5) до прямойМ₁М₂, уравнение которой имеет вид -x+2y-4=0. Подставим данные в формулу(1):

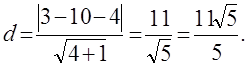
Найдём координаты точек Е иF.

Для точки Е: x=-1/2; y=-5/2; E(-1/2;-5/2).

Для точки F: x=1/2; y=-1/2; F(1/2;-1/2).

Уравнение прямой EF:

y+5/2=-2x-1 или 2x+y+3,5=0.

5.     По каноническому уравнению кривой второго порядка определить тип кривой, начертить её график. Найти координаты фокусов, вершин и центра (для центральной кривой).

 (1)

Воспользуемся параллельным переносом (O’(-3,-1))

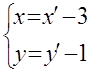 (2)

Подставим (2) в (1), получим

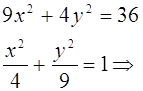
кривая второго порядка является эллипсом.

F₁(c;0); F₂(-c;0).

т.к.

Координаты центра: O’(-3,-1).

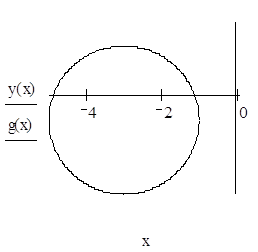
6.         Преобразовать к полярным координатам уравнения линии.

1)

2)

Первое уравнение представляет собой (при любых значениях φ) полюс О. Второе – дает все точки линии, в том числе полюс. Поэтому первое уравнение можно отбросить. Следовательно, получаем:

Линейная алгебра

Матрицы

Ответы на вопросы

1.         Дайте определение обратной матрицы. Какие вы знаете способы вычисления обратной матрицы?

Матрица В называется обратной для матрицы А, если выполняется условие АВ=ВА=Е, где Е – единичная матрица. Способы вычисления обратной матрицы: 1) использование алгебраических дополнений; 2) привести исходную матрицу к ступенчатому виду методом Гаусса, после чего необходимо преобразовать её в единичную .

2.         Как записывается система уравнений в матрично-векторной форме? Как найти решение системы уравнений при помощи обратной матрицы?

Система уравнений в матрично-векторной форме записывается в виде: .

Решение системы уравнения при помощи обратной матрицы:

3.         Сформулируйте, в чем состоит процедура Гаусса и для решения каких линейных задач применяется?

Процедура Гаусса используется для решения систем линейных уравнений и состоит в следующем:

Выполняются элементарные преобразования, вследствие чего можно получить два исхода: