Навигация
Министерство образования и науки Российской Федерации
Курсовая работа
По дисциплине: Высшая математика
(Основы линейного программирования)
На тему: КРАТНЫЕ ИНТЕГРАЛЫ
Выполнил: ______________
Преподаватель:___________
Дата ___________________
Оценка _________________
Подпись ________________
ВОРОНЕЖ 2008
Содержание
1 Кратные интегралы
1.1 Двойной интеграл
1.2 Тройной интеграл
1.3 Кратные интегралы в криволинейных координатах
1.4 Геометрические и физические приложения кратных интегралов
2 Криволинейные и поверхностные интегралы
2.1 Криволинейные интегралы
2.2 Поверхностные интегралы
2.3 Геометрические и физические приложения
Список используемой литературы
1 Кратные интегралы
1.1 Двойной интеграл
Рассмотрим в плоскости Оху замкнутую область D, ограниченную линией L. Разобьем эту область какими-нибудь линиями на п частей ![]() , а соответствующие наибольшие расстояния между точками в каждой из этих частей обозначим d1, d2, ..., dn. Выберем в каждой части
, а соответствующие наибольшие расстояния между точками в каждой из этих частей обозначим d1, d2, ..., dn. Выберем в каждой части ![]() точку Рi.
точку Рi.
Пусть в области D задана функция z = f(x, y). Обозначим через f(P1), f(P2),…, f(Pn) значения этой функции в выбранных точках и составим сумму произведений вида f(Pi)ΔSi:
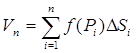 , (1)
, (1)
называемую интегральной суммой для функции f(x, y) в области D.
Если существует один и тот же предел интегральных сумм (1) при ![]() и
и ![]() , не зависящий ни от способа разбиения области D на части, ни от выбора точек Pi в них, то он называется двойным интегралом от функции f(x, y) по области D и обозначается
, не зависящий ни от способа разбиения области D на части, ни от выбора точек Pi в них, то он называется двойным интегралом от функции f(x, y) по области D и обозначается
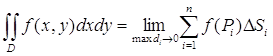 . (2)
. (2)
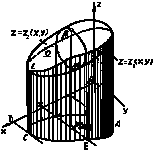
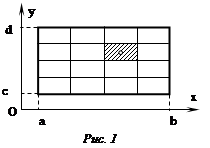
Вычисление двойного интеграла по области D, ограниченной линиями ![]() x = a, x = b ( a < b ), где φ1(х) и φ2(х) непрерывны на [a, b] (рис. 1) сводится к последовательному вычислению двух определенных интегралов, или так называемого двукратного интеграла:
x = a, x = b ( a < b ), где φ1(х) и φ2(х) непрерывны на [a, b] (рис. 1) сводится к последовательному вычислению двух определенных интегралов, или так называемого двукратного интеграла:
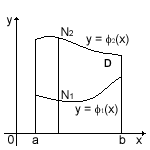
Рис. 1
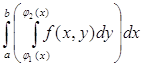 =
= 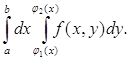 (3)
(3)
1.2 Тройной интеграл
Понятие тройного интеграла вводится по аналогии с двойным интегралом.
Пусть в пространстве задана некоторая область V, ограниченная замкнутой поверхностью S. Зададим в этой замкнутой области непрерывную функцию f(x, y, z). Затем разобьем область V на произвольные части Δvi , считая объем каждой части равным Δvi , и составим интегральную сумму вида
![]() , (4)
, (4)
Предел при ![]() интегральных сумм (11), не зависящий от способа разбиения области V и выбора точек Pi в каждой подобласти этой области, называется тройным интегралом от функции f(x, y, z) по области V:
интегральных сумм (11), не зависящий от способа разбиения области V и выбора точек Pi в каждой подобласти этой области, называется тройным интегралом от функции f(x, y, z) по области V:
![]()
![]() . (5)
. (5)
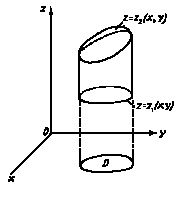
Тройной интеграл от функции f(x,y,z) по области V равен трехкратному интегралу по той же области:
![]()
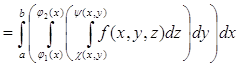 . (6)
. (6)
1.3 Кратные интегралы в криволинейных координатах
Введем на плоскости криволинейные координаты, называемые полярными. Выберем точку О (полюс) и выходящий из нее луч (полярную ось).
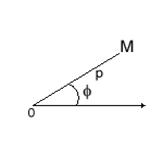
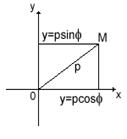
Рис. 2 Рис. 3
Координатами точки М (рис. 2) будут длина отрезка МО – полярный радиус ρ и угол φ между МО и полярной осью: М(ρ,φ). Отметим, что для всех точек плоскости, кроме полюса, ρ > 0, а полярный угол φ будем считать положительным при измерении его в направлении против часовой стрелки и отрицательным – при измерении в противоположном направлении.
Связь между полярными и декартовыми координатами точки М можно задать, если совместить начало декартовой системы координат с полюсом, а положительную полуось Ох – с полярной осью (рис. 3). Тогда x=ρcosφ, у=ρsinφ . Отсюда ![]() , tg
, tg![]() .
.
Зададим в области D, ограниченной кривыми ρ=Φ1 (φ) и ρ=Φ2 (φ), где φ
Похожие работы
... порядок интегрирования ( т.е., скажем, интегрировать сначала по направлению оси Oy, а затем по области плоскости Oxz), то это приведёт к изменению порядка интегрирования в тройном интеграле и к изменению пределов интегрирования по каждой переменной. Рис.3 Рис.4А) Пример. Вычислим тройной интеграл где - область, ограниченная координатными плоскостями и ...
... значения интеграла, основан на «монотонности» интеграла. При этом способе подынтегральную функцию приближают снизу и сверху интегрируемыми в замкнутом виде функциями и , т.е. , (34) Тогда (35) 5. Вычисление интегралов методом Монте-Карло Пусть нам нужно вычислить интеграл: (36) В случае, когда методы Ньютона-Котеса и Гаусса работают плохо, приходится обращаться к вероятностным ...
... пакете………..7 Список использованной литературы……………………......8Теоретическая часть. Численные методы могут использоваться для вычисления кратных интегралов. Ограничимся рассмотрением двойных интегралов вида I= (1) Одним из простейших способов вычисления этого интеграла является метод ячеек. Рассмотрим сначала случай, когда областью интегрирования G является прямоугольник: , ...
... выражения типа дивергенции по п- мерной области и интеграл по ограничивающей ее сверхповерхности S с уравнением L(x,y,z,…)=0. Если придерживаться прежних обозначений, то формула имеет вид (3) Впрочем, Остроградский не применял геометрических образов и терминов, которыми пользуемся мы: геометрия многомерных пространств в то время еще не существовала. В “Мемуаре об исчислении вариаций кратных ...
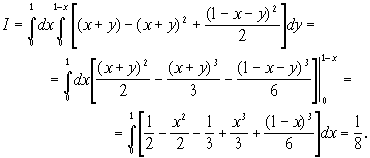

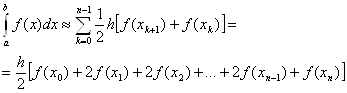


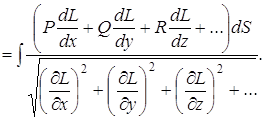
0 комментариев