Навигация
Геометрические и физические приложения
2.3 Геометрические и физические приложения
1) Длина кривой.
Если подынтегральная функция f(x, y, z) ≡ 1, то из определения криволинейного интеграла 1-го рода получаем, что в этом случае он равен длине кривой, по которой ведется интегрирование:
![]() (39)
(39)
2) Масса кривой.
Считая, что подынтегральная функция γ (x, y, z) определяет плотность каждой точки кривой, найдем массу кривой по формуле
![]() (40)
(40)
Пример 6.
Найти массу кривой с линейной плотностью ![]() заданной в полярных координатах уравнением ρ = 4φ, где
заданной в полярных координатах уравнением ρ = 4φ, где ![]()
Решение.
Используем формулу (40) с учетом того, что кривая задана в полярных координатах:
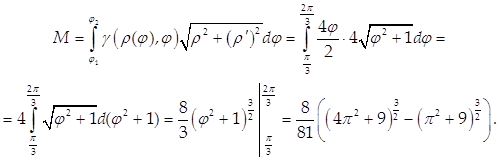
3) Моменты кривой l:
![]() - (41)
- (41)
- статические моменты плоской кривой l относительно осей Ох и Оу;
![]() - (42)
- (42)
- момент инерции пространственной кривой относительно начала координат;
![]() - (43)
- (43)
- моменты инерции кривой относительно координатных осей.
4) Координаты центра масс кривой вычисляются по формулам
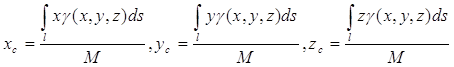 . (44)
. (44)
5) Работа силы ![]() , действующей на точку, движущуюся по кривой (АВ):
, действующей на точку, движущуюся по кривой (АВ):
![]() , (45)
, (45)
Пример 7.
Вычислить работу векторного поля ![]() вдоль отрезка прямой от точки А(-2;-3;1) до точки В(1;4;2).
вдоль отрезка прямой от точки А(-2;-3;1) до точки В(1;4;2).
Решение.
Найдем канонические и параметрические уравнения прямой АВ:
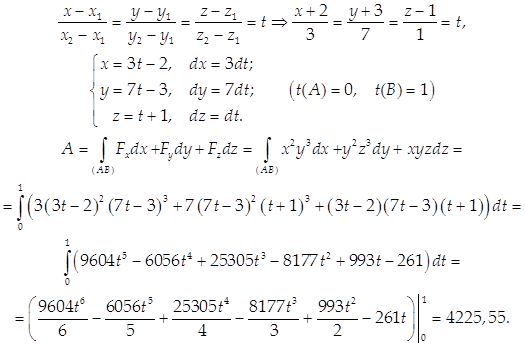
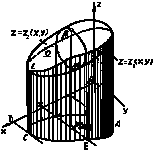
6) Площадь криволинейной поверхности, уравнение которой
z = f(x, y), можно найти в виде:
![]() (46)
(46)
(Ω – проекция S на плоскость Оху).
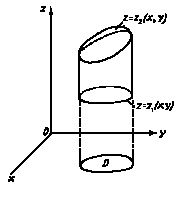
7) Масса поверхности
![]() (47)
(47)
Пример 8.
Найти массу поверхности 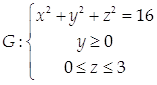 с поверхностной плотностью γ = 2z2 + 3.
с поверхностной плотностью γ = 2z2 + 3.
Решение.

На рассматриваемой поверхности ![]()
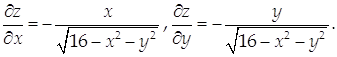 Тогда
Тогда
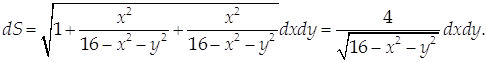
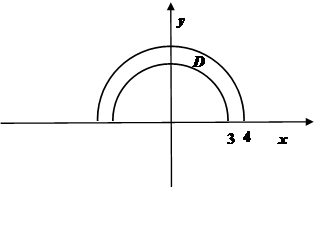
Проекцией D этой поверхности на координатную плоскость Оху является полукольцо с границами в виде дуг концентрических окружностей радиусов 3 и 4.
Применяя формулу (47) и переходя к полярным координатам, получим:
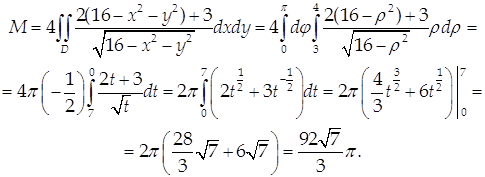
8) Моменты поверхности:
![]() (48) статические моменты поверхности относительно координатных плоскостей Oxy, Oxz, Oyz;
(48) статические моменты поверхности относительно координатных плоскостей Oxy, Oxz, Oyz;
![]() (49)
(49)
- моменты инерции поверхности относительно координатных осей;
![]() - (50)
- (50)
- моменты инерции поверхности относительно координатных плоскостей;
![]() - (51)
- (51)
- момент инерции поверхности относительно начала координат
9) Координаты центра масс поверхности:
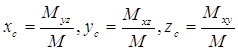 . (52)
. (52)
Список используемой литературы
1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. М.: Наука, 1999.
2. Кудрявцев Л.Д. Краткий курс математического анализа. М.: Наука, 2000.
3. Ильин В.А., Позняк Э.Г. Математический анализ. М.: Наука, 1999.
4. Смирнов В.И. Курс высшей математики.- Т.2. М.: Наука, 2005.
5. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М.: Наука, 2001.
6. Пискунов Н.С. Дифференциальное и интегральное исчисление. – Т.2. М.: Наука, 2001.
7. Сборник задач по математике для втузов. Специальные разделы математического анализа (под редекцией А.В.Ефимова и Б.П.Демидовича). – Т.2. М.: Наука, 2004.
8. Мышкис А.Д. Лекции по высшей математике. М.: Наука, 2003.
9. Титаренко В.И., Выск Н.Д. Кратные, криволинейные и поверхностные интегралы. Теория поля. М.: МАТИ, 2006.
Похожие работы
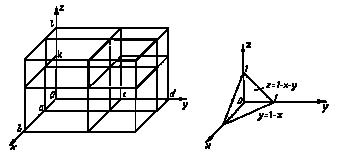
... порядок интегрирования ( т.е., скажем, интегрировать сначала по направлению оси Oy, а затем по области плоскости Oxz), то это приведёт к изменению порядка интегрирования в тройном интеграле и к изменению пределов интегрирования по каждой переменной. Рис.3 Рис.4А) Пример. Вычислим тройной интеграл где - область, ограниченная координатными плоскостями и ...
... значения интеграла, основан на «монотонности» интеграла. При этом способе подынтегральную функцию приближают снизу и сверху интегрируемыми в замкнутом виде функциями и , т.е. , (34) Тогда (35) 5. Вычисление интегралов методом Монте-Карло Пусть нам нужно вычислить интеграл: (36) В случае, когда методы Ньютона-Котеса и Гаусса работают плохо, приходится обращаться к вероятностным ...
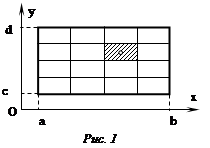
... пакете………..7 Список использованной литературы……………………......8Теоретическая часть. Численные методы могут использоваться для вычисления кратных интегралов. Ограничимся рассмотрением двойных интегралов вида I= (1) Одним из простейших способов вычисления этого интеграла является метод ячеек. Рассмотрим сначала случай, когда областью интегрирования G является прямоугольник: , ...
... выражения типа дивергенции по п- мерной области и интеграл по ограничивающей ее сверхповерхности S с уравнением L(x,y,z,…)=0. Если придерживаться прежних обозначений, то формула имеет вид (3) Впрочем, Остроградский не применял геометрических образов и терминов, которыми пользуемся мы: геометрия многомерных пространств в то время еще не существовала. В “Мемуаре об исчислении вариаций кратных ...

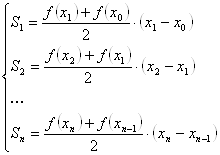
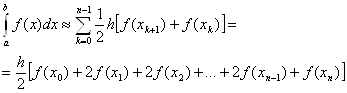


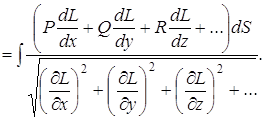
0 комментариев