Навигация
Другие критерии согласия. Критерии согласия для распределения Пуассона
1.5 Другие критерии согласия. Критерии согласия для распределения Пуассона
Еще одна возможность для проверки согласия, которой тоже часто пользуются. Состоит она в том, что проверяют не исходную гипотезу целиком, а какие-либо ее последствие, которое считается важным. Для нормальной случайной величины ξ коэффициент асимметрии равен нулю.
 (5.1)
(5.1)
Поэтому коэффициент асимметрии выборки
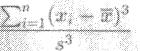 (5.2)
(5.2)
тоже должен быть близок к нулю, если эта выборка – нормальная.
Чтобы судить о том, значимо ли отличается от нуля выборочное значение (5.2), и тем самым, не нарушено ли обязательное для нормального закона соотношение (5.1), надо знать, как распределена статистика (5.2) при гипотезе. Для малых выборок исследование подобных вопросов возможно далеко не всегда и, во всяком случае, требует особого рассмотрения в каждом случае. Иное дело большие выборки.
Есть стандартная методика, которая позволяет справится с этой задачей. Покажем ее действие на другом примере, поскольку о нормальном законе говорилось лишком много. Посмотрим, как можно проверить согласие выборки с распределением Пуассона. Для случайной величины ξ, распределенной по Пуассону
Dξ/Мξ = 1, (5.3)
так как для распределения Пуассона Dξ = Мξ = λ, где λ – параметр распределения. Поэтому если выборка х1, …, хп извлечена из пуассоновской генеральной совокупности, то отношение должно быть близким к 1. Ниже пойдет речь о том как проверить.
![]() (5.4)
(5.4)
Но сначала одно замечание общего характера: такие проверки никак не могут доказать соответствия выборки теоретическому закону даже при неограниченном возрастании числа наблюдений. Причина в том, что соотношение типа (5.1) и (5.3) не являются характеристиками: даже если (5.1) справедливо, оно не означает, что ξ непременно распределено нормально. Это свойство необходимо для нормальности распределения, но не достаточно. То же самое можно сказать о (5.3): это необходимое, но не достаточное условие для того, чтобы распределение было пуассоновским. После этого обсуждения обратимся к изучению свойств статистики (5.4). объем выборки п будет считать большим.
Воспользуемся тем, что при n → ∞ случайные величины S2 – Dξ и х – Мξ стремятся к 0 (закон больших чисел). Поэтому для пуассоновской выборки:
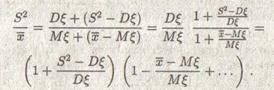
Многоточие заменяет случайную величину, убывающую как n-1. раскрыв скобки, получаем, что:
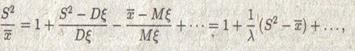
Исследуем при n → ∞ поведение выражения
![]()
главной случайной составляющей дроби
![]()
Без ущерба для точности вывода вместо S2 можно взять случайную величину:
![]()
Тогда вместо S2 – х появляется:
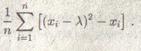
В силу центральной предельной теоремы эта сумма независимых и одинаково распределенных случайных величин распределена приблизительно нормально, с математическим ожиданием:
М[(ξ – λ)2 – ξ] = 0 и дисперсией
![]()
Для вычисления последнего выражения надо знать, что четвертый и третий центральные моменты пуассоновского распределения равны соответственно
![]()
После этого подсчет дает, что D[(ξ – λ)2 – ξ] = 2λ2. Следовательно, статистика (5.4) ![]() распределена приблизительно по закону N(1, 2λ2/ n).
распределена приблизительно по закону N(1, 2λ2/ n).
Зная распределение статистики (5.4) в случае справедливости нулевой гипотезы о принадлежности выборки к распределению Пуассона, можно указать пределы, в которые с вероятностью приблизительно, скажем, 0.99 должно попадать отношение ![]() в случае справедливости гипотезы:
в случае справедливости гипотезы:
![]() (5.5)
(5.5)
где, и0 обозначает квантиль уровня α стандартного нормального распределения.
Если мы хотим использовать это соотношение для практической проверки гипотезы о пуассоновском распределении выборки, надо заметить неизвестное значение λ его оценкой по выборке. Для больших выборок наилучшей является оценка наибольшего правдоподобия. Которая для пуассоновского распределения равна х. следовательно, надо проверить по выборке, выполняется ли соотношение:
![]() (5.6)
(5.6)
Если это неравенство не выполняется, гипотезу о том, что выборка извлечена из распределения Пуассона, следует отвергать на уровне значимости (примерно) 0.01. понятно, что при другом уровне значимости в правой части (5.5) будет стоять другая квантиль и поэтому правая часть (5.6) тоже будет другой.
Поскольку этот способ проверки приближенный, то чем большего объема окажется выборка в нашем распоряжении, тем точнее будет соблюден номинальный уровень значимости. К сожалению, трудно сказать определенно, начиная с каждого n результат такой проверки заслуживает доверия; по-видимому, для этого требуется не менее сотни наблюдений.
Подобным образом может быть проверено любое свойство теоретического распределения, если только мы располагаем достаточно большой выборкой. Главное здесь – выбор самого свойства. Эта характеристика распределения должна быть существенна для дальнейшего. Как правило, знания о типе распределения нужны для того, чтобы на их основе сделать по выборочным данным те или инее выводы. Нередко оказывается, что для справедливости этих выводов особенно важны лишь ее которые свойства теоретического закона распределения. Именно эти свойства и надо в первую очередь проверить.
РАЗДЕЛ II. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ КРИТЕРИЯ СОГЛАСИЯ
Все рассмотренные до сих пор критерии принято относить к группе так называемых параметрических критериев. Применение этих критериев требует знания типа распределения наблюдаемых случайных величин (нормальное, биномиальное, пуассоновское, двумерное нормальное или какое-либо иное) и проверяемая гипотеза касается параметров данных распределений. Прежде чем применять параметрические методы, необходимо убедиться в том, что мы действительно имеем дело с распределением требуемого типа.
Предположение о виде распределения случайной величины – это статистическая гипотеза, которую можно проверить с помощью экспериментальных данных. Критерии, позволяющие решать такого рода задачи, называются критериями согласия – согласия выборочных данных некоторому наперед заданному теоретическому распределению.
При проверке гипотезы о нормальности распределения с неизвестными средним и дисперсией критерий Колмогорова-Смирнова является более мощным, чем критерий ![]() .
.
При проведении данных исследований, в которых реализован ряд критериев проверки согласия эмпирического распределения с теоретической моделью: ![]() Пирсона, отношения правдоподобия, Колмогорова, Смирнова,
Пирсона, отношения правдоподобия, Колмогорова, Смирнова, ![]() и
и ![]() Мизеса, Никулина. Здесь и ниже, когда мы употребляем словосочетание “хорошее согласие”, то подразумеваем, что по всем критериям достигнутый уровень значимости, определяемый соотношением
Мизеса, Никулина. Здесь и ниже, когда мы употребляем словосочетание “хорошее согласие”, то подразумеваем, что по всем критериям достигнутый уровень значимости, определяемый соотношением
![]()
где ![]() - значение статистики критерия, вычисленное по наблюдаемой выборке,
- значение статистики критерия, вычисленное по наблюдаемой выборке, ![]() - плотность предельного распределения статистики соответствующего критерия при справедливости гипотезы
- плотность предельного распределения статистики соответствующего критерия при справедливости гипотезы ![]() , был очень высок:
, был очень высок:
![]() 0,6-0,9
0,6-0,9
Например, на (Приложения рис.2) представлены результаты моделирования распределения статистики ![]() при вычислении оптимальных L-оценок [5] двух параметров нормального распределения при числе интервалов
при вычислении оптимальных L-оценок [5] двух параметров нормального распределения при числе интервалов ![]() . На рисунке приведены построенная в результате моделирования эмпирическая функция распределения статистики
. На рисунке приведены построенная в результате моделирования эмпирическая функция распределения статистики ![]() , функция теоретического
, функция теоретического ![]() -распределения и значения достигнутого уровня значимости
-распределения и значения достигнутого уровня значимости ![]() при проверке согласия по каждому из используемых критериев.
при проверке согласия по каждому из используемых критериев.
Если же оценки параметров искать по точечным выборкам (по исходным негруппированным наблюдениям), то предельные распределения статистики ![]() не являются
не являются ![]() -распределениями. Более того, распределения статистики
-распределениями. Более того, распределения статистики ![]() становятся зависящими от того, как разбивается область определения случайной величины на интервалы [5]. Как выглядят распределения статистики
становятся зависящими от того, как разбивается область определения случайной величины на интервалы [5]. Как выглядят распределения статистики ![]() при использовании ОМП по точечным выборкам по сравнению с
при использовании ОМП по точечным выборкам по сравнению с ![]() -распределениями иллюстрирует (Приложения рис. 3), на котором приведены распределения
-распределениями иллюстрирует (Приложения рис. 3), на котором приведены распределения ![]() при асимптотически оптимальном группировании (АОГ) и при разбиении на интервалы равной вероятности (РВГ) в случае проверки согласия с нормальным распределением с оцениванием двух его параметров и числе интервалов
при асимптотически оптимальном группировании (АОГ) и при разбиении на интервалы равной вероятности (РВГ) в случае проверки согласия с нормальным распределением с оцениванием двух его параметров и числе интервалов ![]() . При оценивании параметров нормального закона по группированной выборке статистика
. При оценивании параметров нормального закона по группированной выборке статистика ![]() подчинялась бы в данном случае
подчинялась бы в данном случае ![]() -распределению. Как подчеркивает (Приложения рис. 3), распределения статистики
-распределению. Как подчеркивает (Приложения рис. 3), распределения статистики ![]() и
и ![]() очень существенно отличаются от
очень существенно отличаются от ![]() -распределения. Игнорирование этого факта на практике часто приводит к неоправданному отклонению проверяемой гипотезы, к увеличению вероятности ошибок первого рода.
-распределения. Игнорирование этого факта на практике часто приводит к неоправданному отклонению проверяемой гипотезы, к увеличению вероятности ошибок первого рода.
Зная предельные распределения ![]() и
и ![]() статистики
статистики ![]() , для любого заданного уровня значимости
, для любого заданного уровня значимости ![]() можно оценить мощность соответствующего критерия, рассматривая её как функцию от числа интервалов
можно оценить мощность соответствующего критерия, рассматривая её как функцию от числа интервалов ![]() при заданном объеме выборки
при заданном объеме выборки ![]() . Было проведено исследование мощности критериев Пирсона и Никулина как функции от
. Было проведено исследование мощности критериев Пирсона и Никулина как функции от ![]() и
и ![]() аналитически и методами статистического моделирования. Причем результаты аналитических вычислений оказались полностью подтвержденными оценками мощности, полученными на основании моделирования.
аналитически и методами статистического моделирования. Причем результаты аналитических вычислений оказались полностью подтвержденными оценками мощности, полученными на основании моделирования.
Величина мощности для критериев типа ![]() может быть вычислена в соответствии с выражением:
может быть вычислена в соответствии с выражением:
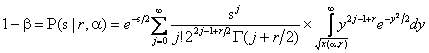
где ![]() - параметр нецентральности,
- параметр нецентральности, ![]() представляет собой
представляет собой ![]() - процентную точку
- процентную точку ![]() -распределения с
-распределения с ![]() степенями свободы (
степенями свободы (![]() - заданная вероятность ошибки первого рода,
- заданная вероятность ошибки первого рода, ![]() - вероятность ошибки второго рода). Все приводимые ниже функции мощности строились при уровне значимости
- вероятность ошибки второго рода). Все приводимые ниже функции мощности строились при уровне значимости ![]() .
.
На (Приложение рис. 4) в зависимости от числа интервалов ![]() при равновероятном и асимптотически оптимальном группировании для объема выборок
при равновероятном и асимптотически оптимальном группировании для объема выборок ![]() , равного 500 и 5000, представлены функции мощности критерия
, равного 500 и 5000, представлены функции мощности критерия ![]() Пирсона при проверке простой гипотезы о согласии с экспоненциальным законом (
Пирсона при проверке простой гипотезы о согласии с экспоненциальным законом (![]() :
: ![]() при
при ![]() ; против
; против ![]() :
: ![]() при
при ![]() ). И в том, и в другом случае с ростом
). И в том, и в другом случае с ростом ![]() мощность падает, но в случае асимптотически оптимального группирования она выше, чем при равновероятном.
мощность падает, но в случае асимптотически оптимального группирования она выше, чем при равновероятном.
Аналогично, на (Приложения рис. 5) приведены функции мощности критерия ![]() Пирсона как функции числа интервалов
Пирсона как функции числа интервалов ![]() для
для ![]() , равного 300 и 2000, при проверке простой гипотезы относительно нормального закона
, равного 300 и 2000, при проверке простой гипотезы относительно нормального закона
(![]() :
: ![]()
при ![]() ,
, ![]() ; против
; против ![]() : нормальный закон при
: нормальный закон при ![]() ,
, ![]() ).
).
На рис. 5 приведены функции мощности критерия ![]() Пирсона при проверке сложной гипотезы о согласии с распределением Вейбулла. Рассматривались гипотеза
Пирсона при проверке сложной гипотезы о согласии с распределением Вейбулла. Рассматривались гипотеза
![]() :
: 
при ![]() ,
, ![]() и близкая альтернатива – распределение Накагами
и близкая альтернатива – распределение Накагами
![]() :
: 
при ![]() ,
, ![]() ,
, ![]()
Рис. 7 иллюстрирует поведение функции мощности критерия типа ![]() Никулина при использовании равновероятного группирования и проверке сложной гипотезы о согласии с нормальным законом
Никулина при использовании равновероятного группирования и проверке сложной гипотезы о согласии с нормальным законом
![]() :
: ![]()
когда в качестве альтернативы рассматривается близкий ему логистический закон
![]() :
: 
при значениях параметров ![]() ,
, ![]() .
.
Если для конкретной выборки мы отклоняем гипотезу о нормальности, и, следовательно, не имеем права пользоваться методами, основанными на нормальности, то для получения статистических выводов можно поступать разными способами. Например, если объем выборки достаточно велик, можно предпочесть использовать параметрические критерии как приближенные. Другой путь состоит в подборе замены переменной, приводящей к нормальному распределению[9]. Третий путь - применение непараметрических критериев.
Пример. Пусть получена следующая выборка 50 значений случайной величины ![]() с неизвестным распределением: (см. Таблица 1)
с неизвестным распределением: (см. Таблица 1)
Проверим гипотезу о том, что эта случайная величина имеет нормальное распределение. После разбиения области изменения выборочных значений на 5 равных интервалов получаем следующие наблюденные и гипотетические частоты:(см. Приложения Таблица 2)
Гипотетические частоты вычислялись для нормального распределения
![]()
с параметрами, оцененными по выборке - соответственно, число степеней свободы статистики критерия равно 5-1-2=2. Выборочное значение статистики равно ![]() , что не выходит за критический 5%-ный предел, равный
, что не выходит за критический 5%-ный предел, равный ![]() . Следовательно, у нас нет оснований отвергнуть гипотезу о нормальности.
. Следовательно, у нас нет оснований отвергнуть гипотезу о нормальности.
В действительности, выборка была получена с помощью датчика случайных чисел, равномерно распределенных на отрезке [0, 100]. Т.е. мы видим, что при данном числе наблюдений (в общем-то, конечно, небольшом для проверки гипотезы о типе распределения) критерий ![]() не обнаруживает отклонения от нормальности в направлении равномерности.
не обнаруживает отклонения от нормальности в направлении равномерности.
Величина статистики одновыборочного критерия Колмогорова - Смирнова равна D=0.11, что также не выходит за 5%-ный предел этого критерия в предположении, что гипотетические средние равны выборочным. Однако в случае неизвестных параметров гипотетического нормального распределения лучше пользоваться модификацией критерия Колмогорова - Смирнова, предложенной Cтефенсом (Лиллифорсом). Но в этом случае значение
![]()
т.е. нет оснований отвергнуть гипотезу и по этому критерию.
Пример. Расчеты, аналогичные предыдущим, проведенные для выборки объема 150 значений случайной величины, равномерно распределенной на отрезке [0, 100], дали значение ![]() , что позволило отвергнуть гипотезу о нормальности на уровне значимости 5%. По критерию Колмогорова - Смирнова гипотеза отвергалась лишь на уровне 10%, а по критерию Лиллифорса - на уровне 1%, что показывает неправомочность применения критерия Колмогорова - Смирнова в данной ситуации.
, что позволило отвергнуть гипотезу о нормальности на уровне значимости 5%. По критерию Колмогорова - Смирнова гипотеза отвергалась лишь на уровне 10%, а по критерию Лиллифорса - на уровне 1%, что показывает неправомочность применения критерия Колмогорова - Смирнова в данной ситуации.
Пример. Расчеты статистик критериев согласия для данных таблицы 1, содержащей 50 выборочных значений длины лепестка ириса разноцветного, приводят к значению статистики ![]() равному 2.1, и значению статистики
равному 2.1, и значению статистики ![]() , равному 0.117. В этом случае гипотеза о нормальности не отвергается ни критерием
, равному 0.117. В этом случае гипотеза о нормальности не отвергается ни критерием ![]() , ни критерием Колмогорова - Смирнова - Лиллифорса.
, ни критерием Колмогорова - Смирнова - Лиллифорса.
Пример. В некоторых классических экспериментах с селекцией гороха Мендель наблюдал частоты различных видов семян, получаемых при скрещивании растений с круглыми желтыми семенами и растений с морщинистыми зелеными семенами. Они приводятся ниже вместе с теоретическими вероятностями, вычисленными в соответствии с теорией наследственности Менделя. (см. Приложения Таблица 3)
В этом случае теоретическое распределение дискретно и известно полностью. Для проверки согласия экспериментальных данных теоретическому распределению используем критерий ![]() для простой гипотезы. Значение статистики, вычисленное по выборке равно
для простой гипотезы. Значение статистики, вычисленное по выборке равно
![]()
что меньше 5%-ного критического значения
![]()
Следовательно, теория наследственности Менделя не противоречит полученным экспериментальным данным.
Наряду с количественными статистическими критериями для определения типа распределения по выборочным данным используются графические методы.
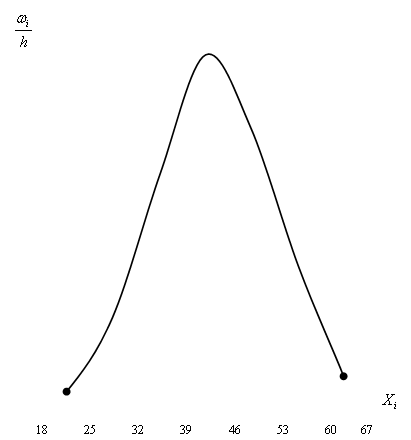
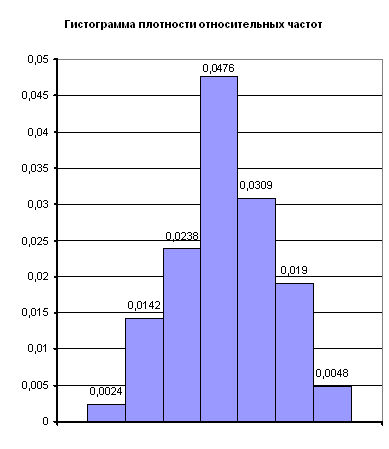
Простейший способ – построение по имеющейся выборке гистограммы относительных частот и на том же графике и в том же масштабе, - кривой плотности нормального распределения с выборочным средним и выборочной дисперсией в качестве параметров. Значительные отклонения от нормальности (сильная асимметрия, бимодальность) легко обнаруживаются на графике.
Пример: Применим этот прием к рассмотренной выше модельной выборке объема n=50, извлеченной из равномерного распределения. На рис. 7 приведена гистограмма и кривая нормальной плотности. Можно сказать, что визуально отклонение от нормальности в пользу равномерности заметно (хотя, как мы видели, статистически значимо при таком числе наблюдений оно не подтверждается).
С точки зрения визуального обнаружения отклонений от нормальности сравнение эмпирической и гипотетической функций распределения гораздо менее наглядно, чем сравнение гистограммы с графиком плотности. Однако обычно сравнивают на сами функции распределения, а обратные нормальные преобразования от них, так называемые пробит-графики. Пробит-график от теоретической нормальной функции распределения представляет собой прямую, а пробит-график эмпирической функции распределения тем ближе к прямой, чем ближе она к нормальной. Этот прием позволяет на первом этапе анализа данных выявить их особенности, выдвинуть гипотезы о характере распределения, решить вопрос о целесообразности замены переменной. (см. Приложения Рис.1 Пример сравнения гистограммы и кривой нормальной плотности.)
Вывод
Критерии согласия основаны на использовании различных мер расстояния между анализируемым эмпирическим распределением и функцией распределения признака в генеральной совокупности. Критериями согласия называют статистические критерии, предназначенные для проверки согласия опытных данных и теоретической модели.
Существует несколько критерий согласия: критерий согласия Колмогорова и омега-квадрат, χ2 Пирсона, χ2 Фишера и другие. Состоятельность критериев Колмогорова и омега-квадрат означает, что любое отличие распределения выборки от теоретического будет с их помощью обнаружено, если наблюдения будут продолжаться достаточно долго. Практическую значимость свойства состоятельности не велика, так как трудно рассчитывать на получение большого числа наблюдений в неизменных условиях, а теоретическое представление о законе распределения, которому должна подчиняться выборка, всегда приближённое. Поэтому точность статистических проверок не должна превышать точность выбранной модели.
В данной курсовой работе было исследовано какие критерии согласия существуют и описано каждую по отдельности, применение критерий согласия на практике.
Приложения
Таблица 1
| 45 | 89 | 93 | 40 | 91 | 60 | 2 | 59 | 87 | 78 |
| 57 | 39 | 50 | 0 | 35 | 91 | 67 | 62 | 25 | 93 |
| 19 | 98 | 55 | 78 | 34 | 45 | 86 | 31 | 15 | 95 |
| 50 | 52 | 35 | 66 | 0 | 44 | 93 | 36 | 29 | 44 |
| 17 | 85 | 17 | 63 | 34 | 43 | 100 | 75 | 84 | 9 |
Таблица 2
| Интервал |
| (20, 40] | (40, 60] | (60, 80] |
|
| Наблюденная частота, nI | 8 | 10 | 12 | 7 | 13 |
| Гипотетическая Частота, npi | 6.1 | 9.7 | 13.4 | 11.6 | 9.2 |
Таблица 3
| Семена | Наблюденная численность | Ожидаемая численность |
| Круглые и желтые | 315 |
|
| Морщинистые и желтые | 101 |
|
| Круглые и зеленые | 108 |
|
| Морщинистые и зеленые | 32 |
|
| Всего | 556 | 556 |
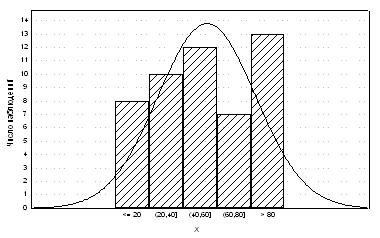
Рис. 1. Пример сравнения гистограммы и кривой нормальной плотности
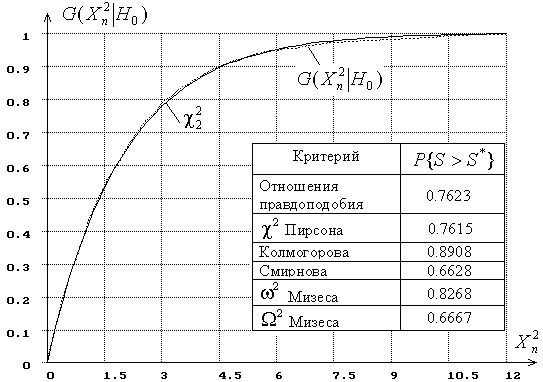
Рис. 2
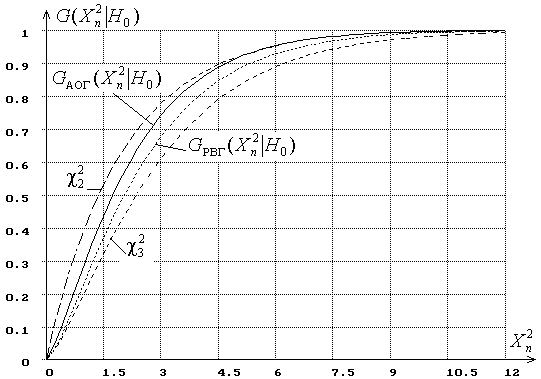
Рис. 3
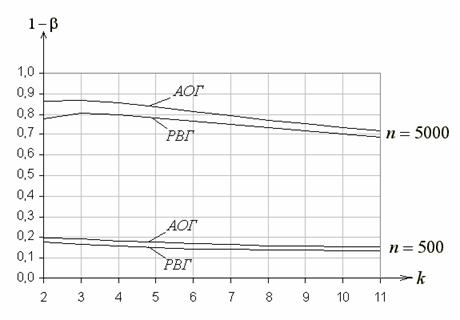
Рис. 4

Рис. 5

Рис. 6
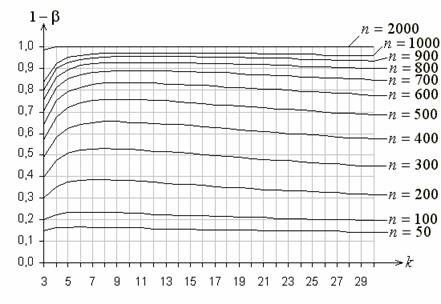
Рис. 7
Список использованной литературы
1. Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере /Под ред. В. Э. Фигурнова. – 3-е изд., перераб. и доп. – М.:ИНФРА – М. 2003. – 544 с., ил.
2. Электронный учебник по дисциплине "Математическая статистика"
В. В. Шеломовский, Мурманский федеральный государственный педагогический университет. http://www.exponenta.ru/educat/systemat/shelomovsky/lab/lab14.asp
3. BaseGroup Labs. Технологии анализа данных. http://www.basegroup.ru/glossary/definitions/chi_square_test/
4. Тюрин Ю.Н. Исследования по непараметрической статистике (непараметрические методы и линейная модель): Автореф. дисс. … д–ра физ.–мат. наук. – М., 1985. – 33 с. – (МГУ).
5. Лемешко Б.Ю., Постовалов С.Н. О зависимости предельных распределений статистик ![]() Пирсона и отношения правдоподобия от способа группирования данных // Заводская лаборатория. 1998. – Т. 64. – № 5. – С.56-63.
Пирсона и отношения правдоподобия от способа группирования данных // Заводская лаборатория. 1998. – Т. 64. – № 5. – С.56-63.
6. Общая теория статистики/ Под редакцией А. А. Спирина, О. Э. Башиной. 1995. – 295 с.
7. Кремер Н.Ш. Теория вероятностей и математическая статистика. – М.: Юнити, 2000. – 543 с.
8. Благовещенский Ю.Н., Самсонова В.П., Дмитриев Е.А. Непараметрические методы в почвенных исследованиях. М.: Наука, 1987.
9. Ширяев А.Н. Вероятность. -- М.: Наука, 1989.
10. Майков Е.В. Математический анализ: Числовые ряды. -- М.: Изд-во МГУ, 1999.
11. Бондарев Б.В. О проверке сложных статистических гипотез // Заводская лаборатория. – 1986. – Т. 52. – № 10. – С. 62-63
Похожие работы
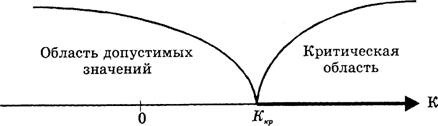
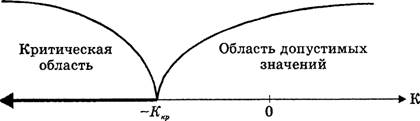
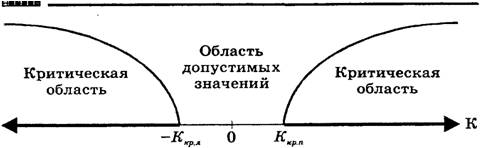
... ошибки первого рода; 3) определить область допустимых значений и так называемую критическую область; 4) принять то или иное решение на основе сравнения фактического и критического значений критерия. Проверка статистических гипотез складывается из следующих этапов: - формулируется в виде статистической гипотезы задача исследования; - выбирается статистическая характеристика гипотезы; - ...
... же для нахождения энергетически оптимальной концентрации эритроцитов в крови, парциального давления в артериальной и венозной крови, определения оптимальных функциональных параметров системы внешнего дыхания и др. 2 Принцип минимального воздействия в эколого-математических моделях Один из способов применения целевой функции состоит в формулировании общего утверждения относительно поведения ...
... в таблицу 4 Таблица 4 21.5 0.0025 28.5 0.0114 35.5 0.0291 42.5 0.0425 49.5 0.0351 56.5 0.0165 63.5 0.0044 3. Критерий согласия (Пирсона) Найду соответствующие вероятности для каждого разряда Из ТВ для нормальной случайной величины (8) Значения функции Лапласа, находим в приложении 2, учебника Вентцель Е.С., Овчаров Л.А., теория вероятностей и её ...
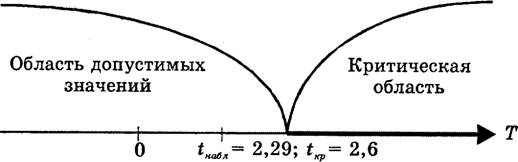
... Таблица 1 Среднее значение интервала, тыс. грн Фактическое количество предприятий 16 9 20 45 24 16 28 24 32 18 36 12 40 6 Всего 100 Тесты для закрепления материала Тест 1 В статистике критерий Стьюдента обозначается: а) критерий; б) ; в) критерий. Тест 2 Мощность критерия – это: а) вероятность отклонения испытуемой нулевой гипотезы, когда правильною является ...
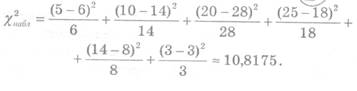
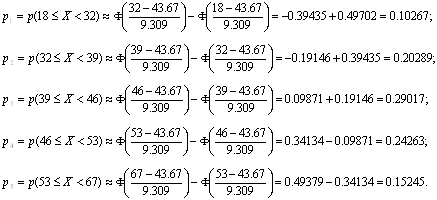
0 комментариев