Мисс Вамп в последний раз видели в ресторане гостиницы в 18 часов вечера, накануне похищения бриллиантов. Ожерелье было тогда на ней

2. Мисс Вамп в последний раз видели в ресторане гостиницы в 18 часов вечера, накануне похищения бриллиантов. Ожерелье было тогда на ней.

3. С 18 часов вечера до 10 часов утра никто из служащих гостиницы не входил в коридор перед номерами, расположенными на первом этаже, и ничего, кроме стука в дверь, не слышали.

4. Между 18 часами вечера и полуночью в гостинице побывало всего 6 посторонних: мистер Браун, мистер Грин, мистер Хилл, мистер Смит, мистер Тейлор и мистер Уайт. Все они приходили к постояльцам, занимавшим номера на первом этаже. Портье, которому из-за его стойки прекрасно виден весь коридор первого этажа, отчетливо запомнил, что каждый из них заходил лишь в один номер, причем ни какие два посетителя не заходили в один и тот же номер. К сожалению, портье не записал, в какой номер заходил каждый из посетителей и до которого часа оставался в гостинице. К тому же, все посетители заходили в гостиницу в различное время: один побывал в ней между 18 и 19 часами, другой между 19 и 20 и т.д. Последний посетитель заходил в гостиницу между 23 к 24 часам. Сэм Силли навестил каждого из шести подозреваемых и выяснил следующее:

5. Достоверно известно, что с 20 до 24 часов мистер Браун принимал у себя дома гостей. Будучи образцовым хозяином мистер Браун от начала до конца своего приема ни на минуту не покидал гостей.

6. Столь же неопровержимо установлено, что с 21 часа до 24 часов мистер Грин находился среди гостей мистера Брауна.

7. Допросить мистера Хилла не удалось, но это не помешало Джони Вуду собрать подробнейшие сведения о подозреваемых и их окружении, снять отпечатки пальцев, следов обуви и т.д. (Попутно, выяснилось одно странное обстоятельство: на мистере Смитте оказались те же ботинки, которые накануне с 18 до 24 часов носил мистер Хилл).

8. Мистер Тейлор с 19 часов 45 минут до 21 часа довольно громко выяснял отношения со своей женой, что могут подтвердить его соседи.

9. Мистер Уайт с 19 до 22 часов находился в театре, а с 23 часов до полуночи присутствовал на заключительной части приема, устроенного мистером Брауном.

Вернувшись в гостиницу, Сэм Силли и Джонни Вуд тщательно осмотрели все номера, расположенные на первом этаже, и установили, что:

10. Все окна плотно закрыты и через них снаружи в гостиницу никто не проникал.

Затем они сравнили все обнаруженные в номерах следы (отпечатки обуви, пальцев, отдельные волоски и т.д.) с теми данными, которые им удалось собрать о подозреваемых. Выяснилось следующее:

11. В номер 5 не заходили ни мистер Смит, ни мистер Тейлор, ни мистер Уайт.

12. Мистер Смит не заходил в номера 1, 3, 6.

13. Мистер Грин не мог быть посетителем номера 3 и номера 6.

Наконец, допросили портье. Приводим выдержку из протокола допроса:

14. Сэм Силли: Вы утверждаете, что незадолго до 20 часов на несколько минут задремали за своей стойкой. Не мог ли кто-нибудь за это время незаметно проникнуть в гостиницу или пробраться из одного номера в другой?

Портье: Входная дверь была заперта, сэр. Я сплю очень чутко, а двери номеров слегка скрипят. Стоило уходившему посетителю хлопнуть дверью, как я бы сразу проснулся. А ведь скрип был очень тихий: так скрипят двери лишь в 1 и 4-м номерах. Затем портье припомнил, что:

15. До 19 часов никто не входил ни в 5-й, ни в 6-й номера.

16. В 20 часов 10 минут в 1 или 3 или 6 номерапришел посетитель, а также, что:

17.Между 22 и 23 часами двери 2, 3 и 6-го номеров не открывались: в эти номера никто не входил и никто не выходил.

Собранные данные позволили сыщикам напасть на след преступника. Из условий 10, 4, 3 и 2 напрашивается почти неопровержимый вывод: бриллиантовое ожерелье похитил один из шести посетителей, а именно тот, который либо вечером, либо ночью заходил в 4-й номер. Можно ли найти преступника, пользуясь всеми данными, собранными Сэмом Силли и Джоном Вудом?

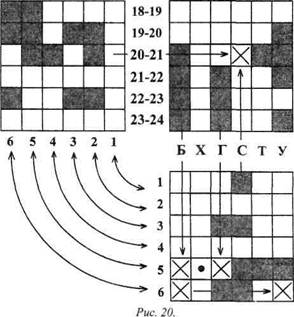
Решение. Одни лишь материалы следствия не позволяют получитьоднознаяного решения ни в одной из таблиц. Но стоит воспользоваться правилом дополнительности, как появляются сразу 5 элементарных запретов (рис. 20).

Эти запреты позволяют найти первое частичное решение: мистер Хилл заходил в номер 5.

Далее задача решается методом треугольника. Уже 10-е частичное решение позволяет установить виновность мистера Брауна, который заходил в номер 4 между 19 и 20 часами. После частичного решения 13 в таблицах I и II остается по 4 пустых клетки, которые не удается заполнить (рис. 21). Но, поскольку мистер Смит заходил в гостиницу раньше или позже мистера Тейлора, что не вызывает противоречия, задача имеет два окончательных решения.

Рассмотрим еще одну задачу, где требуется установить соответствие между множествами, но этих множеств уже 5 (может быть и 6, и 7). Автоматически, пользуясь правилами, решить такую задачу уже не удается. Однако она не менее привлекательна и интересна.

Задача 9. «Укого живет сорока». На одной из улиц дачного поселка только 5 домов. Они окрашены в разные цвета, и занимают их семьи поэта, писателя, критика, журналиста и редактора. В доме каждой семьи живет любимая птичка. Глава семьи получает на завтрак любимый им напиток, после чего отправляется а город, пользуясь любимым способом передвижения. Известно, что:

1)      поэт пользуется велосипедом;

2)      редактор живет в красном доме;

3)      критик живет в крайнем доме слева, а рядом расположен голубой дом;

4)      тот, кто ездит на мотоцикле, живет в среднем доме;

5)      тот, кто живет в зеленом доме, всегда отправляется в город пешком;

6)      зеленый дом расположен справа от белого;

7)      в доме, где живет снегирь, на завтрак всегда бывает молоко;

8)      тот, кто на завтрак получает какао, живет в доме, соседнем с тем домом, где живет синица;

9)      в желтом доме на завтрак подают чай;

10)    живущий рядом с любителем канареек утром пьет чай;

11)    писатель пьет только кофе;

12)    тот, кто ездит на своем автомобиле, любит пить томатный сок;

13)    в доме журналиста живет попугайчик.

 А у кого живет сорока?

Решение. Для решения задачи сразу составим основную таблицу, которую будем заполнять по ходу решения (рис. 22). Воспользуемся условиями 3 и 4. По условию 6 имеем две возможности: 3₁ – зеленый дом №4, 3₂ – зеленный дом №5. Продолжим заполнять основную таблицу, если за истину принять предложение 3₁ (рис. 22, подчеркнуто одной чертой). Из 6 следует, дом №3 – белый; (2,3) – дом №5 красный, тогда дом №1 – жёлтый. Учтем условия 5 и 9; (9; 10) – в голубом доме живут канарейки; 1 в голубом доме живет поэт, который пользуется велосипедом. Из условия 12 следует, что редактор ездит на автомобиле и любит томатный сок.

Где живет писатель? Имеем две возможности:

- П₁: писатель живет в белом доме;

- П₂: писатель живет в зеленом доме.

Продолжим рассуждения, считая верным утверждение П₁ (рис. 22, курсив). Тогда в зеленом доме живет журналист. Из условия 11 следует , что в среднем доме пьют кофе. Из 13 – следует, в доме №4 живет попугайчик.

Рассмотрим условие 7. Молоко на завтрак может быть либо в доме №2, либо в доме №4. Но там не может жить снегирь. Получив противоречивые данные, возвращаемся к гипотезе П₂. Снова условие приводят к противоречию (рис. 23).

Рис 22.

Цвет дома	желтый	голубой	белый	зеленый	красный
Глава семьи	критик	поэт	писатель	журналист	редактор
Напиток	чай			кофе	сок
Способ передвижения		велосипед	мотоцикл	пешком	автомобиль
Птичка		канарейки	попугайчик

Цвет дома	желтый	голубой	белый	зеленый	красный
Глава семьи	критик	поэт	писатель	журналист	редактор
Напиток	чай			кофе	сок
Способ передвижения		велосипед	мотоцикл	пешком	автомобиль
Птичка		канарейки	попугайчик

Рис. 23.

Возвращаемся к гипотезе 3₂. Тогда из 2 следует: дом №1 желтый, а следовательно, в голубом доме живут канарейки. Попробуйте ответить на вопрос: «Где живет поэт?». Два варианта ответа (так как по условию 1, поэт пользуется велосипедом):

- ПТ₁ – поэт живет в голубом доме;

- ПТ₂ – поэт живет в белом доме.

Предположим, что вариант ПТ₁ верен (рис. 24, курсив). Из 12 следует: сок пьют в белом доме. Из 11 следует, что писатель живет в зеленом доме и пьет кофе; в белом доме живет журналист, у которого есть попугайчик (условие 13). По условию 8, какао на завтрак могут получать поэт и редактор. Но у редактора нет соседа, который держит синицу. Значит какао любит поэт, а синица живет у критика.

Условие 7: молоко на завтрак может быть только у редактора. Получаем ответ: сорока живет у писателя. Но нужно проверить ещё гипотезу ПТ₂. Приведет ли она к тому же ответу?

№ дома	1	2	3	4	5
Цвет дома	желтый	голубой	красный	белый	зеленый
Глава семьи	критик	поэт	редактор	журналист	писатель
напиток	чай	какао	молоко	сок	кофе
Способ передвижения		велосипед	мотоцикл	автомобиль	пешком
птичка	синица	канарейки	снегирь	попугайчик	сорока

Рис. 24.

Из 13 следует, хозяин голубого дома пьет сок и ездит на автомобиле.

Из 12 следует, писатель живет в зеленом доме и пьет кофе, тогда в голубом доме живет журналист. Но по условию 13, он держит попугайчика. Получили противоречие, ведь в голубом доме живут канарейки (рис. 25). Итак, ответ задачи единственный: сорока живет у писателя.

№ дома	1	2	3	4	5
Цвет дома	желтый	голубой	красный	белый	зеленый
Глава семьи	критик		редактор	поэт	писатель
напиток	чай	сок			кофе
Способ передвижения		автомобиль	мотоцикл	велосипед	пешком
птичка		канарейки

Рис. 25.

Схематично ход рассуждений изображен на рис. 26.

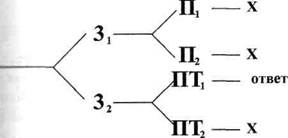
Рис. 26.

Такие задачи могут иметь несколько ответов: число разветвлений в схеме (т.е. количествопринимаемых гипотез) может быть значительно большим, но принцип решения остается таким же. Иногда для решения задачи необязательно заполнять все клетки таблицы, как в приведенном примере.