Навигация
1.2 Тактические задачи
Решение тактических и теоретико-множественных задач заключается в составлении учащимися плана действий, который приводит к правильному ответу. Сложность состоит в том, что выбор нужно сделать из очень большого числа вариантов, т.е. эти возможности не известны учащимся, их нужно придумать.
а)Задачи на перемещение или правильное размещение фигур учащиеся могут решать двумя способами: практическим (действия в перемещении фигур, подборе) и мысленном (обдумывание хода, предугадывание результата, предположение решения). Анализ соотношения способов решения показывает, что практический метод свойственен детям младшей школы. Школьники среднего звена осуществляют поиск решения путем сочетания мысленных и практических действий или только мысленно. Это дает основание для утверждения о возможности приобщения младших школьников к творческой деятельности в ходе решения логических задач. У детей формируется умение вести поиск решения путем предположения, догадки, рассуждений. Рассмотрим простую задачу.
Задача 10. «Иванушка и коварная принцесса».
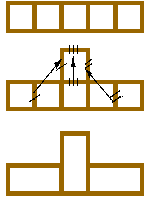
- Задаю тебе последнюю задачу, - сказала принцесса Иванушке, - найди единственно верный путь из этой комнаты в наш зимний сад и сорви для меня самую красивую розу. Из этой комнаты ты пройдешь через левую, или правую, или среднюю дверь во вторую комнату; такие же три вида дверей будут перед тобой при переходе из второй комнаты в третью и из третей – в сад. Учти мои советы, - продолжала принцесса, - первый: из этого зала пройди через правую дверь; второй: из второй комнаты – не через правую дверь, и третий совет: из третей – не через левую дверь. Иванушка знал, что обычно из трех советов принцессы ровно в двух указывают ложное направление, кроме того, служанка принцессы успела шепнуть ему, что надо пройти через дверь каждого вида по одному разу. Как и полагается сказке, принес Иванушка розу и был вознагражден. Какой же маршрут оказался верным?
Решение. Для решения этой задачи нужно рассмотреть всевозможные маршруты, т. к. на избранном пути не должно быть одинаково расположенных дверей, то возможно лишь 6 различных маршрутов (3!). Воспользуемся графами (рис. 27). «Плюс» на соединительном отрезке означает правильный, а «минус» - ложный ответ принцессы. Так как верен один совет, то правильный маршрут тот, который отмечен одним знаком «+» и двумя «-», а именно Л – П – С.
+ – +
П С Л
+ + – + – +
С Л П Л П С
– + – + + +
Л С Л П С П
Рис. 27.
В следующей задаче может быть использована магнитная доска или объемные фигурки зверей, которые можно передвигать по клеткам.
Задача 11. Все звери в зоопарке находятся не в своих клетках. Служителю необходимо как можно быстрее разместить животных по их клеткам. Какое наименьшее число «переселений» должен сделать служитель зоопарка? Учтите, что зверей нельзя помещать вдвоем в одну клетку, так как звери – хишники (рис. 28).
| Надпись на клетке | Лев | Олень | Волк | Крокодил | Леопард |
| Животное | Леопард | Крокодил | Олень | Лев | Волк |
| Вольера | |||||
Рис. 28.
Решение можно оформить в виде следующей таблицы (рис. 29)
| Лев | Олень | Волк | Крокодил | Леопард | Вольер |
| Леопард | Крокодил | Волк | Лев | ||
| Леопард | Крокодил | Олень | Волк | Лев | |
| Леопард | Крокодил | Лев | Олень | Волк | |
| Крокодил | Лев | Олень | Волк | Леопард | |
| Крокодил | Лев | Олень | Волк | Леопард | |
| Крокодил | Лев | Олень | Волк | Леопард | |
| Крокодил | Лев | Олень | Волк | Леопард | |
| Крокодил | Лев | Олень | Волк | Леопард | |
| Крокодил | Лев | Олень | Волк | Леопард | |
| Лев | Олень | Волк | Леопард | Крокодил | |
| Лев | Олень | Волк | Леопард | Крокодил | |
| Лев | Олень | Волк | Леопард | Крокодил | |
| Лев | Олень | Волк | Леопард | Крокодил | |
| Лев | Олень | Волк | Крокодил | Леопард |
Рис. 29.
Задача 12. Три рыцаря, каждый в сопровождении оруженосца, съехались на берегу реки и хотят переправиться на другой берег. Есть лодка, которая может вместить только двух человек. Могут ли переправиться рыцари и их оруженосцы на другой берег при условии, что, оказавшись отдельно от своего рыцаря, ни один оруженосец, не находился бы при этом в обществе других рыцарей?
Такую задачу могут решить учащиеся 6-го класса. Передвигаяя фигурки, можно проверять и пробовать множество вариантов, при этом необходимо записывать ход решения при помощи таблиц, либо при помощи графов.
Решение: этой задачи может быть таким: А, В, С – обозначим рыцарей; а, в, с – их оруженосцев.
А В С А В С . А В С А В С .
а в с . а в с а в . с а в с
А В С в с А В С А В С А В С
а . а в с . а в . с а в с .
. А В С А В С . А В С А В С
а в с а в с . а в с а в с
Ребятам постарше можно предложить следующую задачу. Отличается от предыдущей она только условием, решение же аналогично.
Задача 13. По обычаю одной восточной страны, жене запрещается оставаться без мужа в обществе мужчин, однажды трем супружеским парам понадобилось перебраться на южный берег реки с северного. Единственное подручное средство – лодка, вмещающая двух человек. В какой последовательности они должны были переправиться, чтобы соблюсти строгий обычай?
Такова же схема решения задач на переливание жидкости. Решая такие задачи, школьники учатся планировать свои действия, запоминать ход рассуждений. Эти задачи способствуют развитию настойчивости и сообразительности, развивают аналитическое мышление.
Задача 14. Три сосуда, вместимостью 8, 5, 3 л. стоят на полке. Первый сосуд наполнен водой, а два других пусты. Как с помощью этих сосудов отмерить один литр воды? Как отмерить 4 л. воды?
Решение. Сразу встает вопрос: с чего начать? Имеющиеся сосуды могут предложить два варианта: либо из восьмилитрового сосуда наполним пятилитровый, либо трехлитровый. Нужно учесть, что вода из этих трех сосудов никуда не выливается. Это сокращает число возможных ходов.
Первый способ.
I сосуд (8 л.) 8 3 3 6 6 (1) 1
II сосуд (5л.) 0 5 2 2 0 5 (4)
III сосуд (3л.) 0 0 3 0 2 2 3
Второй способ.
I сосуд (8 л.) 8 5 5 2 2 7 7 (4)
II сосуд (5л.) 0 0 3 3 5 0 1 1
III сосуд (3л.) 0 3 0 3 (1) 1 0 3
Задача 15. Али-Баба хочет попасть в пещеру с сокровищами. Перед пещерой стоит бочка, в крышке которой имеются четыре отверстия, образующие квадрат. Под отверстиями находится по кувшину, в каждом из которых торчит селедка, хвостом вверх или вниз. Али-Баба может просунуть руки в любые два отверстия и определить расположение находящихся под ними селедок, а также повернуть одну или две по своему усмотрению. Если хвосты всех селедок окажутся направленными в одну сторону, то дверь пещеры открывается. После того, как Али-Баба вытащит руки из отверстий, бочка быстро поворачивается и останавливается, причем Али-Баба не в состоянии определить новое соотношение бочки по отношению к старому. Существует ли способ действий, позволяющий Али-Бабе за несколько попыток наверняка открыть дверь?
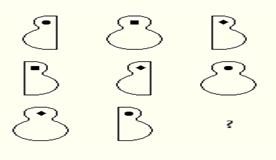
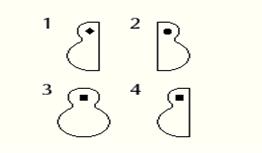
Решение. Для решения необходимо рассмотреть все возможные действия Али-Бабы. Например, по схеме на рисунке 31. Таким образом самое большое после пяти «ходов» Али-Баба сможет попасть в пещеру с сокровищами. Если досконально рассматривать все возможности, то на третьем шаге Али-Баба может просунуть руки в отверстия, стоящие рядом, но это усложнит его дальнейшие действия.
Рассмотрим этот вариант (рис. 30):
Во втором случае – поменяв положение одной селедки, нельзя точно знать, какая из двух комбинаций а) или б) получилась. Следующий ход делается по диагонали. В случае а) нужно изменить положение двух селедок по диагонали и дверь откроется; в случае б) этот «ход» лишний, с его помощью можно определить положение селедок.
Дальше решение идет, как в общем случае, но Али-Баба сделает на один «ход» больше. Нужно сказать, что данная задача довольно сложная. Разбирая ее решение, нужно рассуждать последовательно и доказательно, отвечая на вопросы: «А почему именно так?», «А что будет если…?». На, а потом не трудно выбрать оптимальное решение, т.е самый кортокий путь к решению задачи (рис. 31).
Похожие работы
... сочетаниям". И значительное место в таком построении должно принадлежать широкому применению в процессе обучения младших школьников нестандартных логических задач. Глава II. Методика использования логических задач на уроках математики в начальной школе 2.1 Интегрированное обучение и развитие мышления в простой игре Общее соображение о важности широкого внедрения в школьный урок ...
... не кашалот. IV фигура. Вывод – общеотрицательное суждение. Ситуация 5. Закончите следующий силлогизм и дайте его логическую формулу, определите вид заключения и фигуру силлогизма. Ни одна птица – не млекопитающие. Все млекопитающие – позвоночные. Решение: № Алгоритм Конкретное соответствие данной ситуации предложенному алгоритму 1 Выделение среднего термина и определение фигуры ...
... Задачи: 1. Выявить уровень развития мыслительных операций у детей подготовительной к школе группы. 2. Разработать и апробировать программу развития мыслительных операций у старших дошкольников, посредством логических задач и упражнений у детей экспериментальной группы исследования. 3. Выявить динамику повышения уровня развития мыслительных операций у детей контрольной и ...
... психолого-педагогическую и методическую учебную и специальную литературу по теме исследования. 2) Рассмотрели особенности обучение школьников решению логических задач на уроках информатики. 3) Охарактеризовали особенности использования ИКТ на уроках информатики. 4) Разработали методики использования информационных технологий на уроке информатики с целью обучения школьников решению логических ...
0 комментариев