Задачи на нахождение пересечения или объединение множеств (круги Эйлера)

1.3 Задачи на нахождение пересечения или объединение множеств (круги Эйлера)

Ещё один тип задач – задачи, в которых требуется найти некоторое пересечение множеств или их объеденение, соблюдая условия задачи.

Задача 16. В шахматном турнире учавствовало 7 человек . каждый с каждым сыграл по одной партии. Сколько партий они сыграли?

Решение. При решении этой задачи в счете возможны ошибки, т.е. некоторые партии считаются дважды. Предложите ребятам найти ответ с помощью графов, обозначая каждого ученика точкой, а игры – стрелками. Остается только подсчитать стрелки (рис. 32).

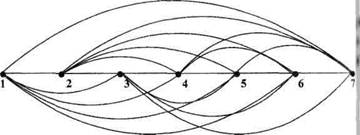
Рис. 32.

Можно оформить задачу в виде турнирной таблицы и подсчитать ее клеточки. Такие методы помогут ребятам объяснить числовое решение задачи:

Число партий =(7*6)/2=21

В дальнейшем школьники легко смогут решать такие задачи и без помощи грофов.

Задача 17. Каждые два из двадцати городов соединены линией воздушного беспересадочного сообщения. Сколько всего воздушных сообщений?

Ответ: 190

Задача 18. В учительской комнате в одну из перемен завязался разговор о журналах. В ходе его выяснилось, что каждый из учителей выписывает два журнала. На каждый из выписываемых журналов подписывается трое. Любая комбинация из двух таких журналов выписывается одним учителем сколько было учителей? Сколько было журналов выписано? Сколько номеров журналов они получили за год, если все журналы были ежемесячными?

Решение заключается в правильном построении графической схемы. Обозначим журналы точками. Каждому журналу соответствует три подписчика, т.е. из каждой точки выходят три ребра, каждое ребро соединяется еще с одной точкой (рис. 33). Каждая пара из полученных трех точек должна быть соединена отрезком. После проведения этих отрезков убеждаемся, что к графу нечего добавить.

Посмотрев на схему, можно сказать, что журналов было четыре, а учителей 6. число журналов в год легко посчитать: 6*2 *12 = 144. Или 4*3*12= 144.

При решении некоторых задач требуются более сложные построения. Пусть ребята придут к ним сами, пусть попробуют использовать уже знакомые им методы.

Еще один метод решения теоретико-множественных задач, с которыми следует познакомит ребят – это круги Эйлера.

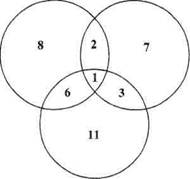
Задача 19. В школе зимой работали 3 секции (лыжная, хоккейная, конькобежная). Всего в секциях занималось 38 учеников. В лыжной - 21 человек, среди которых трое еще занимались коньками, шестеро - еще в хоккейной секции, а один - сразу в трех секциях. В конькобежной секции было 13 человек, среди которых пятеро занимались сразу в двух секциях. Сколько человек заномалось в хоккейной секции?

 хоккей коньки

Лыжи

Рис. 34.

Метод Эйлера (рис. 34) является незаменимым при решении некоторых задач, а также значительно упрощает рассуждения. Однако не всегда к задаче, с первого взгляда похожей на эту, нужно строить такую схему. Прежде, чем приступить к решению задачи, нужно проанализировать условия. Иногда с помощью арифметических действий решить такую задачу легче.

Задача 20. Одна швейцарская община насчитывает 50 членов. Родной язык всех 50 членов общины – немецкий, но 20 из них говорят еще по-итальянски, 35 из них владеют французским и еще 10 не знают ни итальянского, ни французского. Сколько членов общины говорят и по-французски, и по-итальянски?

Решение. 50 – 10 = 40 - владеют иностранным языком (кроме немецкого). 20 + 35 = 55 и 55 – 40 = 15 – членов общины говорят и по-французски, и по-итальянски (рис. 35).

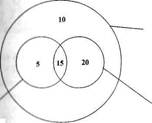
Рис. 35.

1.4 Буквенные ребусы и задачи со звездочками

Методом подбора и рассмотрения различных вариантов решаются буквенные ребусы и примеры со звездочками.

Такие задачи различны по сложности и схеме решения. Рассмотрим один такой пример.

Например:

к а ф т а н б у л о к с о л д а т и

к а ф т а н б ы л о * * ч е р т и

т р и ш к а м н о г о * *

 * *

 *

 * * * *

 * * * * *

 7 * * * * *

 * * * *

 * * * * *

 * * * 7 7 7 0

б у к в а. 6 = с л о в о

Задача 21. Г + О = Л – О = В О = Л – О = М – К = А

Решение: Г + О = Л – О = В * О = М – К = А. Т.к буква О встречается в примере больше других, выбор вариантов начпем с нее, О ≠ 0, т.к. О ≠А, а В • О = А;

О ≠ 9, т.к. Г + О = А, кроме того, Л > О на А единиц

О ≠ 8, т.к. Г + О = А и Л > О получим, что Л = А = 9.

Из равенства В • О = А следует, что нужно исключить также варианты О = 7, О = 6, О = 5 иначе при минимальном В = 2 (В•О) – двузначное число. Пусть О = 4, тогда В = 2, а А = 8, но Л – 4 = 8 не имеет смысл ни при одном Л, значит О ≠ 4.

Пусть О = 3, тогда в = 2 или В = 3. Если В = 2, то А = 6, Л = 9, но Г = 3 = О. Если В = 3, то А = 9, Л = 12. Значит О ≠ 3

Пусть О = 2. Г + 2 = Л – 2 = В, 2 = М – К = А.

Если В = 3, то А = 6, Г + 2 = 6, Г = 4, Л – 2 = 6, Л = 8, М – К = 6, М = 7 и К = 1.

Если В = 4, то А = 8, Л = 10 (противоречит условию, что Л – цифра).

Пусть О = 1. Тогда Г + 1 = Л – 1 = В, 1 = М – К = А, В = А, что неверно.

Задача имеет единственное решение:

Г = 4; О = 2; В = 3; М = 7; К = 1; А = 6; Л = 8.

4 + 2 = 8 – 2 = 3 • 2 = 8 – 2 = 7 – 1 = 6.

Задача 22. Перед началом бегов на ипподроме четыре знатока из числа зрителей обсуждали шансы фаворитов А, В или С.

Первый: Заезд выиграет А или С.

Второй: Если А придет третьим, то С не выиграет.

Третий: Если А будет вторым, то выиграет В.

Четвертый: Вторым придет А или В.

После заезда выяснилось, что три фаворита А, В, С действительно заняли первые три места и что все четыре утверждения знатоков оказались истинными. Как фавориты поделили между собой три первых места?

Решение. Эта задача по схеме решения похожа на задачу 10. Возможны 6 вариантов исхода заезда (з!):

А В С

А С В (4)

В С А (1), (4)

В А О (1)

С А В (3)

С В А (2).

Справа указаны утверждения, которым противоречат эти варианты. Всем условиям задачи удовлетворяет расположение мест, при котором фаворит А пришел первым, В – вторым и С – третьим.

Эта задача не является сложной, она может быть использована в качестве тренировочной, намечающей подход к решению задач, которые требуют установить истинность или ложность множества высказываний.

1.5 Истинностные задачи

Задачи, в которых требуется установить истинность или ложность высказываний назовем истинностными задачами.

Задача 23. В одном старинном задачнике суд Париса описан следующим образом: богини Гера, Афродита и Афина пришли к юному Парису, чтобы тот решил, кто из них прекраснее. Представ перед Парисом, богинивысказали следующие утверждения:

1.      Афродита: Я самая прекрасная.

2.      Афина: Афродита не самая прекрасная.

3.      Гера: Я самая прекрасная.

4.      Афродита: Гера не самая прекрасная.

5.      Афина: Я самая прекрасная.

Парис, прилегший отдохнуть на обочине дороги, не счел нужным даже снять платок, которым прикрыл глаза от яркого солнца. Но богини были настойчивы, и ему во что бы то ни стало, нужно было решить, кто из них самая прекрасная. Парис предположил, что все утверждения прекраснейшей из богинь истинны, а все остальные утверждения двух остальных богинь ложны. Мог ли Парис,исходя из такого предположения, выпести то решение, которое ожидали от него богини, и если мог, то кто из богинь самая прекрасная?

Решение. Для удобства решения высказывания в тексте задачи пронумерованы:

1 – 5. Составим таблицу (рис. 36)

	Афродита	Афина	Гера
1
2
3
4
5

Рис. 36.

Поочередно предполагая каждую богиню самой прекрасной, проверим, не приведет ли это предположение к противоречию с условием задачи. «+» - истинное высказывание, «-» - ложное. Пусть Афина самая прекрасная из богинь. Тогда высказывание 5 и 2 истинны, а все остальные ложны. Но если ложно высказывание 3, тогда 4 должно быть истинно, и Афродита говорит правду, получили противоречие условию, что правду говорит только прекраснейшая из богинь. Значит, первоначальное предположение неверно: Афина не самая прекрасная. Рассуждая аналогично, приходим к выводу, что самая прекраснейшая из богинь – Афродита.

Задача имеет единственное решение.

Задача 24. До царя Гороха дошла молва, что наконец-то убили Змея Горыныча. Царь знал, что это мог сделать Илья Муромец, Алеша Попович или Добрыня Никитич. Вызвал царь к себе богатырей. И вот они, запыленные, явились ко двору. Стал спрашивать их царь. Трижды каждый богатырь ответ держал.

Добрыня Никитич:

- Я не убивал Змея.

- Я выезжал в заморские страны.

- Змея убил Алеша Попович.

Илья Муромец:

- Змея убил Алеша Попович.

- Если бы я убил его, то не сказал бы.

- Много еще на земле нечистой силы осталось.

Алеша Попович:

- Не убивал я Змея Горыныча.

- Я не ищу, какой бы подвиг совершить.

- И взаправду Добрыня Никитич в заморские страны уезжал.

Царь узнал также, что дважды говорил правду каждый богатырь, а один раз луковал. Кто же убил Змея Горыныча?

Ответ: Муромец.