Навигация
Следовательно, исходное решение не является оптимальным и его можно улучшить
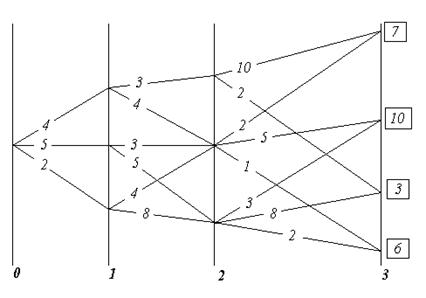
Переход от одного решения транспортной задачи к другому.
Наличие положительной оценки свободной клетки (![]() ) при проверке решения на оптимальность свидетельствует о том, что полученное решение не оптимально и для уменьшения значения целевой функции надо перейти к другому решению. При этом надо перераспределить грузы, перемещая их из занятых клеток в свободные. Свободная клетка становится занятой, а одна из ранее занятых клеток – свободной.
) при проверке решения на оптимальность свидетельствует о том, что полученное решение не оптимально и для уменьшения значения целевой функции надо перейти к другому решению. При этом надо перераспределить грузы, перемещая их из занятых клеток в свободные. Свободная клетка становится занятой, а одна из ранее занятых клеток – свободной.
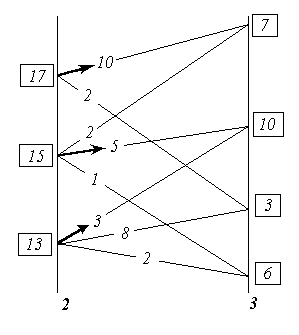
Для свободной клетки Δ15 = 1![]() 0 строится цикл (цепь, многоугольник), все вершины которого, кроме одной, находятся в занятых клетках; углы прямые, число вершин четное. Около свободной клетки цикла ставится знак (+), затем поочередно проставляют знаки (-) и (+). У вершин со знаком (-) выбирают минимальный груз, его прибавляют к грузам, стоящим у вершин со знаком (+), и отнимают от грузов у вершин со знаком (-). В результате перераспределения груза получим новое решение. Это решение проверяем на оптимальность, и так далее до тех пор, пока не получим оптимальное решение.
0 строится цикл (цепь, многоугольник), все вершины которого, кроме одной, находятся в занятых клетках; углы прямые, число вершин четное. Около свободной клетки цикла ставится знак (+), затем поочередно проставляют знаки (-) и (+). У вершин со знаком (-) выбирают минимальный груз, его прибавляют к грузам, стоящим у вершин со знаком (+), и отнимают от грузов у вершин со знаком (-). В результате перераспределения груза получим новое решение. Это решение проверяем на оптимальность, и так далее до тех пор, пока не получим оптимальное решение.
Х2 =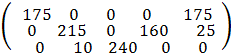
Стоимость перевозки при исходном решении составляет
f2 = 175 * 5 + 215 * 10 + 10 * 20 + 240 * 10 + 160 * 6 + 175 * 8 + 25 * 4 = 8085.
Проверим полученное решение на оптимальность. Для этого запишем его в распределительную таблицу, приведенную ниже, найдем потенциалы занятых и оценки свободных клеток.
|
ai | 1 | 2 | 3 | 4 | 5 | ||
| 175 | 225 | 240 | 160 | 200 | 𝛼i | ||
| 1 | 350 | 5 175 | 15 | 18 | 16 | 8 175 | 0 |
| 2 | 400 | 6 | 10 215 | 15 | 6 160 | 4 25 | -4 |
| 3 | 250 | 25 | 20 10 | 10 240 | 15 | 18 | 0 |
| 𝛽i | 5 | 14 | 10 | 10 | 8 | ||
Для клетки (1,1) : ![]() 1 +
1 + ![]() 1 = 5,
1 = 5, ![]() 1 = 0,
1 = 0, ![]() 1 = 5
1 = 5
Для клетки (1,5) : ![]() 1 +
1 + ![]() 5 = 8,
5 = 8, ![]() 1 = 0,
1 = 0, ![]() 5 = 8
5 = 8
Для клетки (2,5) : ![]() 2 +
2 + ![]() = 4,
= 4, ![]() = -4,
= -4, ![]() = 8
= 8
Для клетки (2,4) : ![]() 2 +
2 + ![]() = 6,
= 6, ![]() 2 = -4,
2 = -4, ![]() 4 = 10
4 = 10
Для клетки (2,2) : ![]() 2 +
2 + ![]() = 10,
= 10, ![]() 2 = -4,
2 = -4, ![]() = 14
= 14
Для клетки (3,3) : ![]() +
+ ![]() = 10,
= 10, ![]() 3 = 0,
3 = 0, ![]() 3 = 10
3 = 10
Найденные значения потенциалов заносим в таблицу. Вычисляем оценки свободных клеток:
Δ12 = ![]() 1 +
1 + ![]() – с 12 = 0 + 14 – 15 = - 1
– с 12 = 0 + 14 – 15 = - 1![]() 0
0
Δ13 = ![]() 1 +
1 + ![]() – с 13 = 0 + 10 – 18 = - 8
– с 13 = 0 + 10 – 18 = - 8 ![]() 0
0
Δ14 = ![]() 1 +
1 + ![]() – с 14 = 0 + 10 – 16 = - 6
– с 14 = 0 + 10 – 16 = - 6 ![]() 0
0
Δ21 = ![]() +
+ ![]() – с 21 = -4 + 5 – 6 = - 5
– с 21 = -4 + 5 – 6 = - 5 ![]() 0
0
Δ23 = ![]() +
+ ![]() – с 23 = - 4 + 10 – 15 = - 9
– с 23 = - 4 + 10 – 15 = - 9 ![]() 0
0
Δ31 = ![]() +
+ ![]() – с 31 = 0 + 5 – 25 = - 20
– с 31 = 0 + 5 – 25 = - 20 ![]() 0
0
Δ34 = ![]() +
+ ![]() – с 34 = 0 + 10 – 15 = - 5
– с 34 = 0 + 10 – 15 = - 5 ![]() 0
0
Δ35 = ![]() +
+ ![]() – с 35 = 0 + 8 – 18 = - 10
– с 35 = 0 + 8 – 18 = - 10 ![]() 0
0
Все оценки свободных клеток отрицательные, следовательно, найденное решение оптимальное. Итак,
Хорт =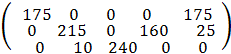
Стоимость транспортных расходов равна
Fmin= 175 * 5 + 215 * 10 + 10 * 20 + 240 * 10 + 160 * 6 + 175 * 8 + 25 * 4 = 8085.
По сравнению с исходным решением, транспортные расходы уменьшились на 175 усл.ед. (8260 – 8085 = 175).
Задачи 41–50. Составить экономико-математическую модель. Найти решение задачи линейного программирования при помощи средств Excel на ПК.
48. В суточном рационе кормления крупного рогатого скота должно быть не менее 20 кормовых единиц, не менее 2000 г белков и не менее 100 г кальция. Для кормления используют сено, силос, корнеплоды и концентраты. Содержание питательных веществ в 1 кг каждого вида корма, а также его себестоимость представлены в таблице. Составить кормовой рацион минимальной стоимости.
| Содержание питательных веществ в 1 кг корма | Корм | |||
| Сено | Силос | Корнеплоды | Концентрат | |
| Кормовая единица | 0,5 | 0,2 | 6 | 0,8 |
| Белки, г | 40 | 10 | 12 | 200 |
| Кальций, г | 5 | 4 | 3 | 1 |
| Себестоимость 1 кг корма, ден. ед. | 2 | 1 | 2 | 4 |
Решение
Обозначим через
· х1 – количество сена,
· х2 - количество силоса,
· х3 - количество корнеплодов,
· х4 - количество концентрата.
Ограничения можно выразить соотношением:
ограничения по кормовой единице-
0,5 * х1 + 0,2 * х2 + 6 * х3 + 0,8 х4 ≥ 20. (1)
ограничения по белкам –
40* х1 + 10 * х2 + 12 * х3 + 200 * х4 ≥ 2000. (2)
ограничения по кальцию –
5 * х1 + 4 * х2 + 3 * х3 + х4 ≥ 100. (3)
Очевидно, что
![]() (4)
(4)
Требование составить кормовой рацион минимальной стоимости определяет целевую функцию:
F = 2 * х1 + х2 + 2 * х3 + 4 * х4 ![]() ( min)
( min)
Требуется найти х1, х2, х3, х4, минимизирующие целевую функцию и удовлетворяющие ограничениям (1)–(4).
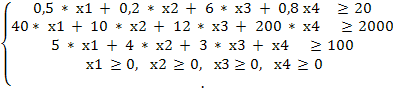
F = 2 * х1 + х2 + 2 * х3 + 4 * х4 ![]() ( min)
( min)
Решаем задачу линейного программирования, использую EXCEL.
Порядок выполнения работы:
1 Загрузили Excel
2 Объединив ячейки А1:В1, пишем текст «Задание № 48»
3 Объединив ячейки А3:G3, пишем текст «Расчет кормового рациона минимальной стоимости»
4 В ячейку А4 пишем текст «Питательные вещества в 1 кг корма»
5 В ячейку А5 пишем текст «кормовая единица»
6 В ячейку А6 пишем текст «Белки, г»
7 В ячейку А7 пишем текст «Кальций, г»
8 В ячейку А8 пишем текст «Себестоимость 1 кг корма, ден.ед.»
9 В ячейку А8 пишем текст «Себестоимость 1 кг корма, ден.ед.»
10 Объдинив ячейки А9:А12, пишем текст «Количество»
11 В ячейку В4 пишем текст «Сено»
12 В ячейку С4 пишем текст «Силос»
13 В ячейку D4 пишем текст «Корнеплоды»
14 В ячейку E4 пишем текст «Корнеплоды»
15 В ячейку F4 пишем текст «функции ограничения»
16 В ячейку G4 пишем текст «Минимальный суточный рацион»
17 В ячейку G4 пишем текст «Минимальный суточный рацион»
18 В ячейку B9 пишем текст «Х1 - сена»
19 В ячейку B10 пишем текст «Х2 - силоса»
20 В ячейку B11 пишем текст «Х3 - корнеплодов»
21 В ячейку B12 пишем текст «Х4 - концентрата»
22 Объдинив ячейки А13:B13, пишем текст «Целевая функция F»
23 В ячейки B5: В7 пишем числа 0,5; 40; 5
24 В ячейки С5: С7 пишем числа 0,2; 10; 4
25 В ячейки D5: D7 пишем числа 6; 12; 3
26 В ячейки E5: E7 пишем числа 0.8; 200; 1
27 В ячейки G5: G7 пишем числа 200; 2000; 100
28 В ячейки B8: E8 пишем числа 2; 1; 2; 4
29 В ячейку F5 пишем формулу =B5*C9+C5*C10+D5*C11+E5*C12
30 В ячейку F6 пишем формулу =B6*C9+C6*C10+D6*C11+E6*C12
31 В ячейку F7 пишем формулу=B7*C9+C7*C10+D7*C11+E7*C12
32 В ячейку С13 пишем формулу =B8*C9+C8*C10+D8*C11+E8*C12
33 Сервис – Поиск решения
34 Установить целевую функцию $C$13
35 Минимальному значению
36 Изменяя ячейки $C$9 : $C$12
36 Ограничения : $C$9 ≥ 0, $C$10 ≥ 0, $C$11 ≥ 0, $C$11 ≥ 0,
$F$5 ≥ $G$5 , $F$6 ≥ $G$6 , $F$7 ≥ $G$7
37 Выполнить
38 Читаем результат : С9 = 0 (х1), С10 = 21,72 (х2),
С11 = 1,43 (х3), С12 = 8,83 (х4),
С13 = 59,9 (F – целевая функция)
Ниже приводится расчетная таблица, полученная в EXCEL:
Задание № 48
| Расчет кормового рациона минимальной стоимости | ||||||
| Питательные вещества в 1 кг корма | Сено | Силос | Корнеплоды | Концент рат | функции ограничения | Минимальный суточный рацион |
| кормовая единица | 0,50 | 0,20 | 6,00 | 0,80 | 20,00 | 20,00 |
| Белки, г | 40,00 | 10,00 | 12,00 | 200,00 | 2000,00 | 2000,00 |
| Кальций, г | 5,00 | 4,00 | 3,00 | 1,00 | 100,00 | 100,00 |
| Себестоимость 1 кг корма, ден.ед. | 2,00 | 1,00 | 2,00 | 4,00 | ||
| Количество | Х1 - сена | 0 | ||||
| Х2 - силоса | 21,72 | |||||
| Х3 - корнеплодов | 1,43 | |||||
| Х4 - концент рата | 8,83 | |||||
| Целевая функция F | 59,90 | |||||
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986.
2. Красс М.С. Математика для экономических специальностей. – М.: Инфа-М, 1998.
3. Кузнецов Ю.Н. Математическое программирование. – М.: Высшая школа, 1980.
4. Общий курс высшей математики для экономистов: Учебник/Под ред. В.И. Ермакова. – М.: ИНФРА-М, 2002.
5. Высшая математика для экономистов/Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 1997.
Похожие работы
... при условии выпуска Х1изделий А1 и Х2 изделий А2 составляет F = 30Х₁ +49Х₂ По своему экономическому содержанию переменные Х1 и Х2 могут принимать только лишь неотрицательные значения: Х1, Х2 ≥0. Таким образом, приходим к следующей математической задаче: среди всех неотрицательных решений системы неравенств (1.1) требуется найти такое, при котором функция F = 30Х₁ +49Х&# ...
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
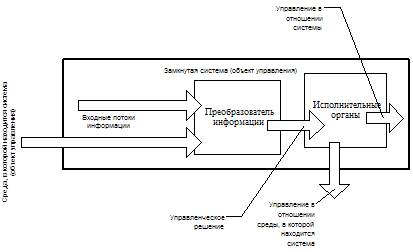
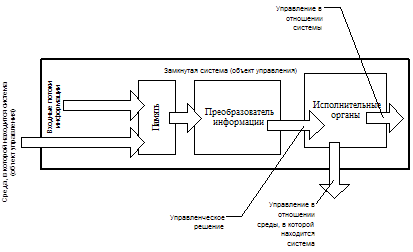
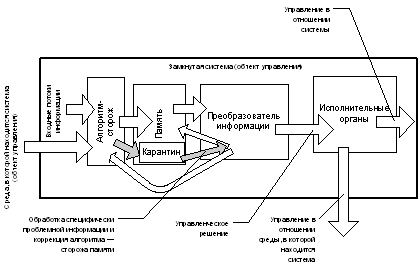
... за собой её гибель, либо требующие подключения к процессу самоуправления суперсистемы иерархически высшего управления. Так соборный интеллект видится индивидуальному интеллекту с точки зрения достаточно общей теории управления; возможно, что кому-то всё это, высказанное о соборных интеллектах, представляется бредом, но обратитесь тогда к любому специалисту по вычислительной технике: примитивная ...
... -педагогическая или научно-техническая проблема, являющаяся новым научным вкладом в теорию определенной области знаний (педагогику, технику и другие). 4. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ ВЫПОЛНЕНИЯ ВЫПУСКНОЙ КВАЛИФИКАЦИОННОЙ РАБОТЫ БАКАЛАВРА ФИЗИКО-МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ ПРОФИЛЬ ИНФОРМАТИКА 4.1. Положение о выпускной квалификационной работе бакалавра физико-математического образования: ...
 bi
bi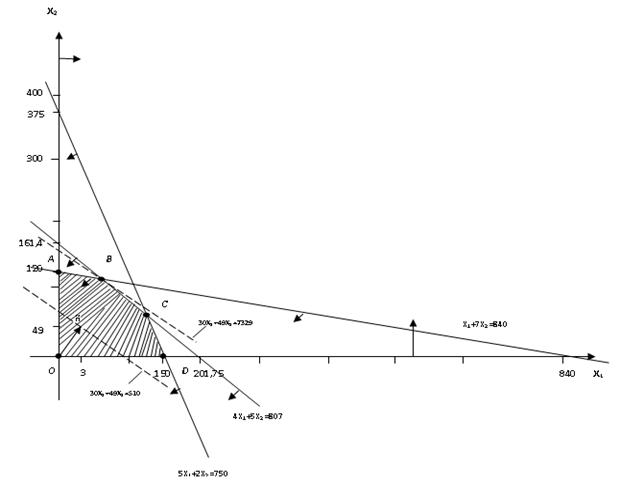





0 комментариев