Навигация
Необходимые исследования зависимостей в MathCad
4. Необходимые исследования зависимостей в MathCad
Для исследования зависимости диаметра балки от P3, необходимо, каждый раз в новом окне MathCad, равномерно изменять значения силы P3 и соответственно полученные значения диаметра балки d.
Аналогично находим зависимости максимального прогиба балки от L4, для этого изменяем значения длины L4 и полученные при этом значения максимального прогиба балки.
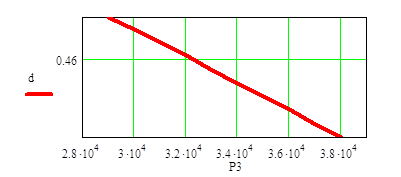
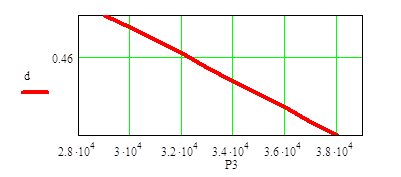
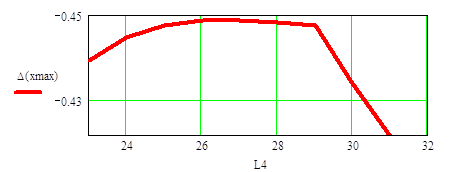
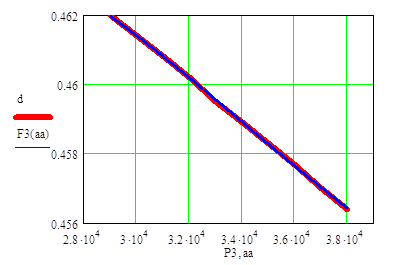
Строим график зависимости силы P3 от диаметра балки d, а также длины L4 от максимального прогиба балки.
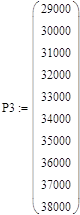
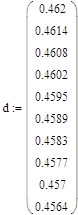
где:
- P3 – сила, действующая на балку;
- d – диаметр балки
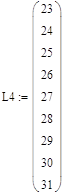

где:
- L4 – длины участка;
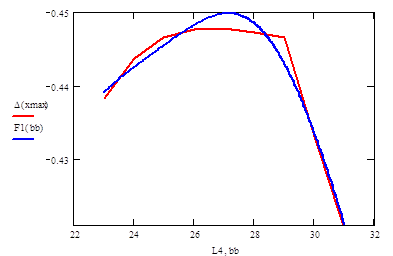
- ∆(xmax) –максимальный прогиб балки

5. Аппроксимация
Находим аппроксимирующую функцию для зависимости диаметра балки от P3. Для этого нам необходимо определить набор функций с помощью которых будем аппроксимировать. Воспользуемся встроенной функцией linfit для определения вектора коэффициентов аппроксимирующей функции. Построить график.
Аналогично для зависимости максимальный прогиб балки от L4
Определяем набор функций с помощью которых будем аппроксимировать

Определяем вектор коэффициентов аппроксимирующей функции
![]()

![]()
![]()
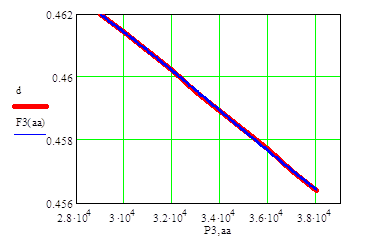
где:
- P3 – сила, действующая на балку;
- d – диаметр балки
-F3(аа)–аппроксимирующая функция
-(аа) –ранжированная переменная
Определяем набор функций с помощью которых будем аппроксимировать
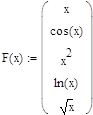
Определяем вектор коэффициентов аппроксимирующей функции
![]()
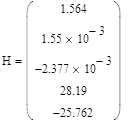
![]()
![]()
 м
м
где:
- L4 – длины участка;
- ∆(xmax) –максимальный прогиб балки
-F1(bb)–аппроксимирующая функция
-(bb) –ранжированная переменная
6. Вывод по проделанным исследованиям
В результате проделанных опытов в курсовой работе, была получена зависимость диаметра балки от силы P3, максимального прогиба балки от длины L4.
Построен график, где показано, что при увеличении силы P3 диаметр d балки уменьшается пропорционально.
На графике зависимости минимального прогиба балки ∆(xmax) от длинны L4 получили: на участке от 23 до 25 функция ведет себя логарифмически, на участке от 25 до 29 функция ведет себя линейно, в дальнейшем функция убывает линейно.
Найдены аппроксимирующие функции. Которые помогут нам найти аналитическую зависимость диаметра балки от P3 и максимального прогиба балки от L4.
Заключение
При разработке данной курсовой работы нам необходимо было изучить: математическое моделирование, его свойства, основные понятия, классификация, алгоритмический анализ задачи и описание исследования задачи в MathCAD.
Я научился работать с пакетом MathCAD, её приложениями и компонентами. Система MathCAD является популярной программой, где можно строить графики, решать сложные дифференциальные, линейные и интегральные уравнения. Таким образом, работа в среде MathCAD даёт значительное повышение точности в расчётах, облегчает процесс программирования при вычислении функций и даёт возможность создания различных документов.
Список литературы
1)Макаров Инженерные расчеты в MathCAD(c.295)
2)Дарков А.В.,Шпиро Г.С. Сопротивление материалов Москва 1989г.
3)Винокуров Е.Ф.,Балыкин М.К., Голубев И.А Справочник по сопротивлению материалов –Мн.:Наука и техника,1988-464с.(с21-23).
4) Токочаков В. И. Практическое пособие по теме "Решение систем алгебраических и дифференциальных уравнений в среде Mathcad для студентов всех специальностей дневного и заочного отделений. - Гомель: ГГТУ, 2000.
5) Яблонский А. А. Курс теоретической механики, ч.II.– М.,1966 г.
6) Тарасик В. П. Математическое моделирование технических систем:
Учебник для вузов. – Мн.: ДизайнПРО, 1997. – 640с.: ил..
7) Останина А.М. Применение математических методов и ВМ.Мн.:1985
Приложения 1
Постановка задачи.
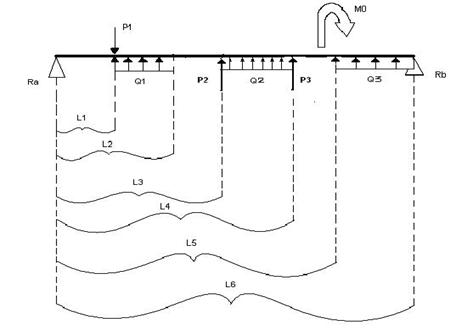

Построение эпюр поперечной силы Q
![]()
![]()
![]()
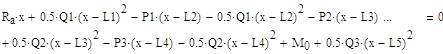
![]()
![]()
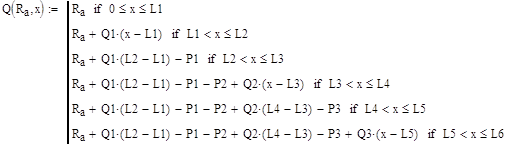
![]()

Построение эпюр поперечной силы М


Нахождение экстремальных значений изгибающего момента
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Определение размеров сечения балки

Определение перемещения балки

Прогиб балки
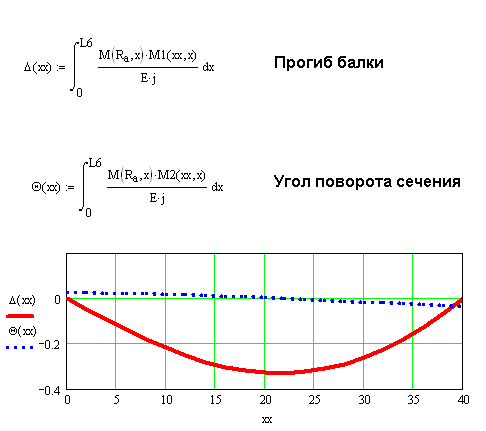
Нахождение экстремальных значений прогиба балки
![]()
![]()
![]()
![]()
![]()
![]()



Необходимые исследования зависимостей
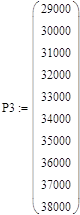
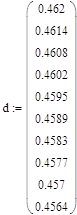
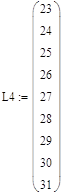

Аппроксимация

![]()
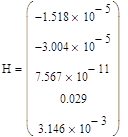
![]()
![]()
![]()

![]()

![]()
![]()
![]()
Похожие работы
... гидродинамического режима системы могут изменяться виды моделей [1]. Цель данной курсовой работы – создать математическую модель процесса получения эмульгатора (применяемого для стабилизации эмульсий «масло в воде») из масла и триэтаноламина и дать характеристику этой модели. Математическое моделирование данного процесса заключается в расчёте значений концентраций реагентов и величин потоков на ...
... воспринимаются даже на высоком научном уровне. Стремление упростить материал вряд ли целесообразно. Глава 3. Методические рекомендации курса «Математические основы моделирования 3D объектов» базового курса «компьютерное моделирование» для студентов педагогических ВУЗов специальности преподаватель информатики §1. Принципы построения электронного учебника Прежде чем рассмотреть ...
... некие ресурсы. То есть технический объект реализует в себе единство затрат и выигрыша. Их отношение лежит в основе практически всех систем оценки эффективности. Понятие «модель технического объекта», на наш взгляд, непосредственно связана с необходимостью рассмотрения категории идеального. Идеал в общественных науках, в искусстве определяется энциклопедическим словарем как «идея, понятие, ...
... Кроме того, техническое (инженерное) творчество довольно часто приносит еще дополнительное моральное и материальное вознаграждение и глубокое удовлетворение полученными результатами. Понятия, связанные с творчеством и техникой. Технический объект и технология Общественная жизнь любой страны, любого народа не может развиваться в нужном направлении без творческой деятельности масс. На основании ...



0 комментариев