Навигация
Матрицы. Дифференциальные уравнения
ВЕКТОРЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
Определение. Вектором называется направленный отрезок прямой. Точка ![]() называется началом вектора
называется началом вектора ![]() , а точка
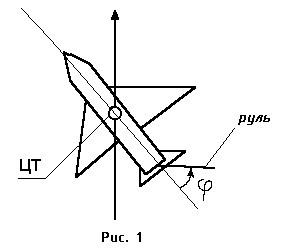
, а точка ![]() – его концом (рис. 1).
– его концом (рис. 1).
Обозначения: ![]() ,
, ![]() .
.

Определение. Длина вектора называется его модулем и обозначается ![]() ,
, ![]() .
.
Определение. Координатами вектора ![]() называются координаты его конечной точки. На плоскости Oxy
называются координаты его конечной точки. На плоскости Oxy ![]() ; в пространстве Oxyz
; в пространстве Oxyz ![]() .
.
Определение. Суммой и разностью векторов ![]() и
и ![]() являются соответственно векторы
являются соответственно векторы
![]() ;
;
![]() ;
;
произведение вектора ![]() на число l есть вектор
на число l есть вектор
![]() .
.
Определение. Длина вектора равна корню квадратному из суммы квадратов его координат:
![]() (на плоскости);
(на плоскости);
![]() (в пространстве).
(в пространстве).
Определение. Расстояние d между двумя точками A и B можно рассматривать как длину вектора ![]() , т.е.
, т.е.
![]() (на плоскости);
(на плоскости);
![]() (в пространстве).
(в пространстве).
Определение. Если два вектора ![]() и
и ![]() перпендикулярны, то
перпендикулярны, то
![]() (на плоскости);
(на плоскости);
![]() (в пространстве).
(в пространстве).
Определение Вектор X называется собственным вектором линейного оператора A (матрицы A), если найдется такое число l, что AX=lX.
Число l называется собственным значением оператора A, заданного матрицей A, т.е. собственные значения находятся из характеристического уравнения ![]() .
.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Определение Обыкновенное дифференциальное уравнение – уравнение, связывающее искомую функцию одной переменной и производные различных порядков данной функции.
Определение Порядок старшей производной – порядок дифференциального уравнения.
Определение Решение дифференциального уравнения – такая функция y=y(x), которая при подстановке ее в это уравнение обращает его в тождество.
Определение Задача нахождения решения дифференциального уравнения называется задачей интегрирования данного дифференциального уравнения.
Определение Общее решение дифференциального уравнения n- го порядка называется такое его решение ![]() , которое является функцией переменной x и n постоянных. Частное решение при конкретных значениях
, которое является функцией переменной x и n постоянных. Частное решение при конкретных значениях ![]() .
.
Определение Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде
![]() .
.
Определение Д.у. первого порядка называется однородным, если оно может быть представлено в виде
![]() .
.
(Для решения используется замена t=y/x)/
Определение Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид
![]() (линейное неоднородное).
(линейное неоднородное).
(Сначала решаем уравнение ![]() - линейное однородное, находим y и подставляем в исходное).
- линейное однородное, находим y и подставляем в исходное).
Определение Уравнение вида
![]()
называется уравнением Бернулли.
(Для решения используется замена ![]() ).
).
![]() =0
=0
(Для решения этого уравнения составляем характеристическое уравнение ![]() ).
).
Теорема 1) Пусть характеристическое уравнение имеет действительные корни l1 и l2, причем ![]() . Тогда общее решение уравнения имеет вид
. Тогда общее решение уравнения имеет вид
![]() (С1, С2 – некоторые числа).
(С1, С2 – некоторые числа).
2) Если характеристическое уравнение имеет один корень l (кратности 2),то общее решение имеет вид
![]() (С1, С2 – некоторые числа).
(С1, С2 – некоторые числа).
3) Если характеристическое уравнение не имеет действительных корней, то общее решение имеет вид
![]() , где
, где
![]() , С1, С2 – некоторые числа.
, С1, С2 – некоторые числа.
НЕОБХОДИМЫЕ ФОРМУЛЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ О КАСАТЕЛЬНОЙ
Общее уравнение прямой:
Ax+By+C=0Уравнение прямой с угловым коэффициентом:
y=kx+b
(k=tgj коэффициент прямой равен тангенсу угла наклона этой прямой)
Если две прямые y=k1x+b1 и y=k2+b2 параллельны, то k1=k2.
Если две прямые y=k1x+b1 и y=k2+b2 перпендикулярны, то k1*k2=-1.
Уравнение прямой, проходящей через данную точку в данном направлении(известен коэффициент k):
Пусть прямая проходит через точку M1(x1;y1) и образует с осью Ox угол ![]()
y-y1=k(x-x1)
Уравнение прямой, проходящей через две данные точки M1(x1;y1) и M2(x2;y2):
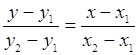
Уравнение касательной к кривой y=f(x) в точке x0 примет вид
y-f(x0)=f¢(x0)(x-x0)
Геометрический смысл производной:
f¢(x0)=k=tga
(производная f¢(x0) есть угловой коэффициент(тангенс угла наклона) касательной, проведенной к кривой y=f(x) в точке x0)
МАТРИЦЫ
Определение: Матрицей размера m![]() n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.
n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.
Матрица размера m![]() n:
n:
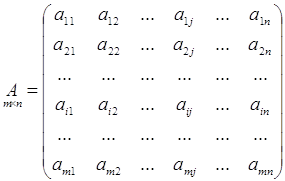 .
.
Виды матриц
Определение: Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой, а из одного столбца – матрицей (вектором)- столбцом.
Пример:
![]() ;
; 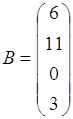 .
.
Определение: Матрица называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n.
Пример:
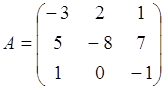 - квадратная матрица третьего порядка.
- квадратная матрица третьего порядка.
Определение: Элементы матрицы aij, у которых номер столбца равен номеру строки (i=j), называются диагональными и образуют главную диагональ матрицы.
Определение: Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.
Пример:
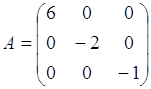 - диагональная матрица третьего порядка.
- диагональная матрица третьего порядка.
Определение: Если у диагональной матрицы n-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n-го порядка, она обозначается буквой E.
Пример:
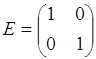 - единичная матрица второго порядка;
- единичная матрица второго порядка;
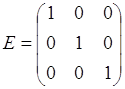 - единичная матрица третьего порядка.
- единичная матрица третьего порядка.
Определение: Матрица любого размера называется нулевой, если все элементы равны нулю.
Операции над матрицами1. Умножение матрицы на число
Каждый элемент матрицы умножается на это число.
Пример:
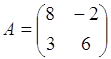 ,
0,5
,
0,5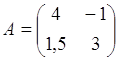 .
.
2. Сложение матриц
!!! Можно складывать матрицы только одинаковых размеров.
Матрицы складываются поэлементно.
Пример:
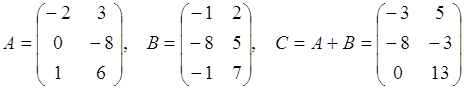 .
.
3. Вычитание матриц
!!! Можно вычитать матрицы только одинаковых размеров.
Матрицы вычитаются поэлементно.
Пример:
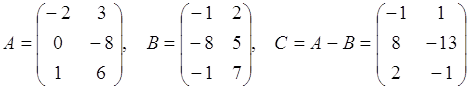 .
.
4. Умножение матриц
!!! Матрицу А можно умножить на матрицу В, если число столбцов матрицы А равно числу строк матрицы В.
Произведением матрицы ![]() называется такая матрица
называется такая матрица ![]() , каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В.
, каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В.
Похожие работы
... в момент t, образует пространство выхода системы. Множество всех значений, которые может принять вектор состояния x в момент t, образует пространство состояний системы. 3.3. Описание непрерывных систем с помощью системы дифференциальных уравнений В любой момент времени t состояние системы является функцией начального состояния x(t0) и вектора входа m(t0, t), то есть x(t)=F[x(t0); m(t0; t)], ...
... популяции обязательно вырождаются, причем независимо от начального распределения особей по возрасту. В завершение рассмотрим пример. Одной из классических моделей динамики популяций является так называемая логистическая модель или модель Ферхюльста, которая описывается дифференциальным уравнением с начальным условием , где , см., например, [5, c. 14]. Если учитывать ограниченность времени жизни ...
... с единицами измерений физических величин в системе MathCAD? 11. Подробно охарактеризуйте текстовые, графические и математические блоки. Лекция №2. Задачи линейной алгебры и решение дифференциальных уравнений в среде MathCAD В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами. Панель операторов с матрицами находится на панели Math. ...
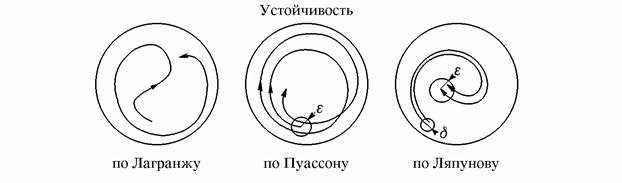
... начальным условиям . Пусть — характеристическое уравнение для определения мультипликаторов. Так как , то оно принимает вид , где . 2. Устойчивость решений систем дифференциальных уравнений. 2.1. Устойчивость по Ляпунову. Вводя определение устойчивости по Лагранжу и Пуассону в пункте 1.3, описывались свойства одной отдельно взятой траектории. Понятие устойчивости по Ляпунову характеризует ...


0 комментариев