Навигация
Процес квадратування коренів
1.4 Процес квадратування коренів
Покажемо тепер, як можна просто скласти рівняння, коренями якого є квадрати коренів даного алгебраїчного рівняння, взяті зі знаком мінус. Остання обставина викликається міркуваннями зручності, щоб за можливістю уникнути появи від’ємних коефіцієнтів. Процес переходу від коренів xk (k=1, 2, …, n) до коренів
yk=-xk2 (1)
для короткості зватимемо квадратуванням коренів.
Нехай
P(x)=a0xn+a1xn-1+…+an=0
- дане рівняння, де a0≠0.
Позначуючи через x1, x2, …, xn корені цього рівняння, матимемо:
P(x)=a0(x-x1)(x-x2)…(x-xn).
Звідси
P(-x)=(-1)na0(x+x1)(x+x2)…(x-xn).
Відповідно,
P(x)P(-x)=(-1)na02(x2-x12)(x2-x22)…(x2-xn2). (2)
Вважаючи
y=-x2
в наслідок формули (2) отримаємо поліном
Q(y)=P(x)P(-x),
Коренями якого є числа
yk=-xk2 (k=1, 2, …, n).
Так як
P(-x)=(-1)n(a0xn-a1xn-1+a2xn-1-…+(-1)nan),
то, роблячи перемноження поліномів P(x) і P(-x), матимемо:
P(x)P(-x)=(-1)n(a02x2n-(a12-2a0a2)x2n-2+(a22-2a1a3+2a0a4)x2n-4-...+(-1)nan2).
Відповідно, рівнянням, що цікавить нас є
Q(x)=A0yn+A1yn-1+A2yn-2+…+An=0
де
A0=a02,
A1=a12-2a0a2,
A2=a22-2a1a3+2a0a4,
…
An=an2.
Правило: При квадрату ванні коренів кожен коефіцієнт перетвореного рівняння дорівнює квадрату попереднього коефіцієнта, мінус подвоєний добуток сусідніх із ним коефіцієнтів, плюс подвоєний добуток слідуючих в порядку близькості коефіцієнтів і т. д., причому якщо потрібний коефіцієнт відсутній, то він вважається рівним нулю.
1.5 Використання методу для випадку дійсних різних корені
Нехай корені x1, x2, …, xn рівняння n-ного ступеню з дійсними коефіцієнтами
![]() (1)
(1)
дійсні і різні за модулем. Розташуймо їх в порядку спадання модулів:
![]() .
.
Покроково використовуючи метод квадратування коренів, складемо рівняння
![]() , (2)
, (2)
коренями якого слугують числа
![]() (k=1, 2, …, n). (3)
(k=1, 2, …, n). (3)
Якщо p досить велике, то корені y1, y2, …, yn є відділеними та на підставі частини 1.2. могуть бути визначені з ланцюжку лінійних рівнянь
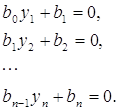
Звідси маємо:
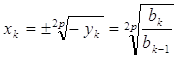 (k=1, 2, …, n); (4)
(k=1, 2, …, n); (4)
знаки коренів визначаються грубою прикидкою, при підстановці в дане рівняння, або на підставі співвідношень між коренями та коефіцієнтами рівнянь. Процес квадратування коренів зазвичай продовжується доти, доки подвоєні добутки не перестануть впливати на перші головні члени коефіцієнтів перетвореного рівняння. Правило. Процес квадратування коренів варто припинити, якщо коефіцієнти деякого перетвореного рівняння в межах точності обчислень дорівнюють квадратам відповідних коефіцієнтів наступного перетвореного рівняння за рахунок відсутності подвоєних добутків. Дійсно, якщо перетворене рівняння, що відповідає ступеню 2p+1, має вигляд
![]()
та виконані співвідношення
![]() (k=0, 1, 2, …, n),
(k=0, 1, 2, …, n),
то, вочевидь, отримаємо:
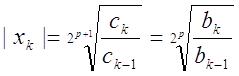 .
.
Таким чином, при цих обставинах ми не зможемо збільшити точність обчислення коренів. Так як при використання метода Лобачевського-Греффе коефіцієнти перетворених рівнянь, взагалі кажучи, швидко зростають, то корисно виділяти порядки їх, записуючі коефіцієнти в стандартній формі α*10m, де |α|<10 та m – ціле число.
1.6 Формули методу
Як сказано в ідеї методу
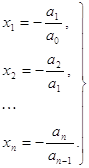 (1)
(1)
Отже, якщо корені рівняння
![]()
відділені, то вони наближено визначаються з ланцюжку рівнянь
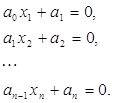 ;
;
причому точність цих коренів залежить від того, наскільки малі за модулем величини ![]() k в співвідношеннях
k в співвідношеннях
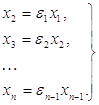 .
.
При квадратуванні коренів коефіцієнти при змінних, як було сказано, дорівнюють
A0=a02,
A1=a12-2a0a2,
A2=a22-2a1a3+2a0a4,
…
An=an2.
Коротше можна записати:
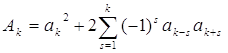 (k=0, 1, 2, …, n),
(k=0, 1, 2, …, n),
де мається на увазі as=0 при s<0 і s>n.
Після квадратування коренів отримаємо рівняння:
![]() ,
,
де
![]() ;
;
отже
![]() . (2)
. (2)
Виходячи з системи (1)
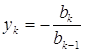 (3)
(3)
З формул (2) та (3) отримуємо
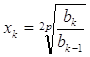 .
.
2. Конкретні приклади використання методу
2.1 Приклад
Методом Лобачевского-Греффе знайти корені рівняння
![]() .
.
Рішення. Результати квадратування коренів, залишаючи чотири значущі цифри розміщені в таблиці 1.
| Ступені | коеф. при x3 | коеф. при x2 | коеф. при x1 | коеф. при x0 |
| 1 | 1 | 0 | -3 | 1 |
| 2 | 1 | 6 | 9 | 1 |
| 4 | 1 | 18 | 69 | 1 |
| 8 | 1 | 1,86*102 | 4,725*103 | 1 |
| 16 | 1 | 2,515*104 | 2,233*107 | 1 |
| 32 | 1 | 5,878*108 | 4,986*1014 | 1 |
| 64 | 1 | 3,445*1017 | 2,486*1029 | 1 |
| 128 | 1 | 1,187*1035 | 6.180*1058 | 1 |
Зупиняючись на 64-ому ступеню коренів, матимемо:
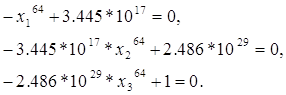
Звідси
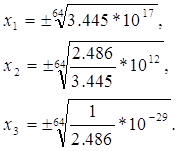
Логарифмуючи, отримаємо:
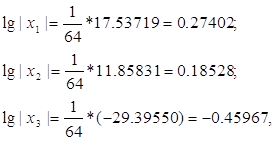
а, отже,
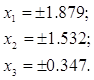
Для визначення знаків коренів зауважимо, що згідно з правилом Декарта наше рівняння має один негативний корінь та два позитивних корені, причому
![]()
Тому найбільшим за модулем має бути негативний корінь, і ми остаточно маємо:

причому співвідношення ![]() виконано в межах заданої точності. Для порівняння можна взяти точні значення коренів, отримані за формулою Кардана:
виконано в межах заданої точності. Для порівняння можна взяти точні значення коренів, отримані за формулою Кардана:
x1=2cos160°=-1.87938;
x2=2cos40°=-1.53208;
x3=2cos80°=0.34730.
Зауважимо, що в нашому випадку обчислення коренів настільки спростилося завдяки тому, що крайні коефіцієнти рівняння дорівнюють 1. Взагалі, при використанні метода Лобачевского-Греффе радимо попередньо перетворити рівняння так, щоб старший коефіцієнт рівняння дорівнював 1, а вільний член рівняння дорівнював ±1.
Програма обчислення коренів рівняння наведена в ДодаткуA.
Висновки
В роботі ми розглянули метод Лобачевского-Греффе, навчилися використовувати його для розв’язання алгебраїчних рівнянь.
Вивчивши алгоритм методу, склали програму мовою C++, що спрощує його обчислення. Вона докладно описується в додаткуA.
Перелік посилань
1. „Основы вычислительной математики”; Б. П. Демидович, І. А. Марон; „Государственное издательство физико-математической литературы”, Москва, 1960
2. „Математический анализ”; А. Я. Дороговцев; „Либідь”, Київ, 1993
3. „Программирование на языке C++”; С. А. Калоєров; „Юго-восток”, Донецьк, 2004
Додаток A
Скласти програму для обчислення коренів алгебраїчного рівняння
Код програми, що обчислює корені алгебраїчного рівняння методом Лобачевского-Греффе.
#include<iostream.h>
#include<math.h>
void main()
{int j,s,k,i,n,step,izo;
double summ,akms,akps,b;
cout<<"Введите степень уравненийа\n";
cin>>step;
n=step+1;
double*a=new double[n];
double*A=new double[n];
double*x=new double[step];
cout<<"Введите коэффициенты при переменных\n";
for(i=0;i<=step;i++)
cin>>a[i];
for(j=2;j<=128;j*=2)
{for(k=0;k<=step;k++)
{summ=0.0;
for(s=1;s<=k;s++)
{if(((k-s)<0)||((k-s)>step)) akms=0.0; else
akms=a[k-s];
if(((k+s)<0)||((k+s)>step)) akms=0.0; else
akps=a[k+s];
summ=summ+pow(-1,s)*akms*akps;
}
A[k]=a[k]*a[k]+2*summ;
}
for(i=0;i<=step;i++)
a[i]=A[i];
}
b=1.0/128.0;
for(i=0;i<step;i++)
x[i]=pow((a[i+1]/a[i]),b);
for(i=0;i<step;i++)
{izo=i+1;
cout<<"X"<<izo<<"="<<x[i]<<"\n";
}
cout<<"Подставьте корни в исходное уравнение, меньайа знаки корней на противоположные, если они не обращают его в тождество";
}
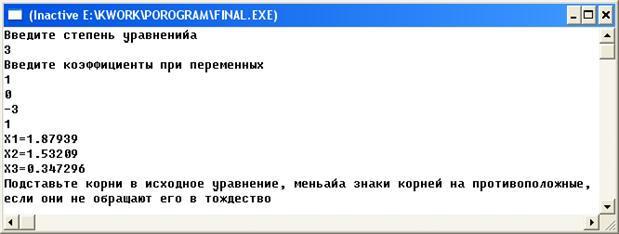
Результат роботи програми
Похожие работы
... Звідси . Власний вектор можна обчислити з умов ортогональності: Звідси Або Після нормування остаточно отримаємо: 2.6 приклади задач, що зводяться до відшукання власних значень та власних векторів матриці Задача 1 Дослідимо тривісне напруження стану елемента тіла, представленого на малюнку. Матриця напруги для нього має вигляд Якщо ...
0 комментариев