Навигация
Метод наименьших квадратов в случае интегральной и дискретной нормы Гаусса
Метод наименьших квадратов в случае интегральной и дискретной нормы Гаусса
1. Постановка задачи
При решении многих задач физики и других прикладных наук возникает необходимость вместо функции ![]() , рассматривать функцию
, рассматривать функцию ![]() , представляющую функцию
, представляющую функцию ![]() как можно «хорошо».
как можно «хорошо».
Например: ![]() может быть, в частности, и непрерывной функцией на
может быть, в частности, и непрерывной функцией на ![]() , а
, а ![]() соответствующая
соответствующая ![]() - алгебраическим или тригонометрическим многочленом, который «достаточно хорошо» приближает функцию
- алгебраическим или тригонометрическим многочленом, который «достаточно хорошо» приближает функцию ![]() .
.
Например: всякую ![]() функцию из
функцию из ![]() можно представить приближённо соответствующим многочленом степени
можно представить приближённо соответствующим многочленом степени ![]() с помощью формулы Тейлора:
с помощью формулы Тейлора:
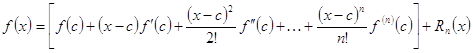 (1)
(1)
т.е.
![]() ;
; ![]() (2)
(2)
где ![]() ,
, ![]() - многочлен степени
- многочлен степени ![]() , приближающий функцию
, приближающий функцию ![]() ,
, ![]() - остаточный член. Ясно, что
- остаточный член. Ясно, что
![]() (3)
(3)
т.е. ![]() - характеризует абсолютную погрешность приближения функции
- характеризует абсолютную погрешность приближения функции ![]() многочленом
многочленом ![]() в точке
в точке ![]() .
.
Известно также, что ![]() можно приблизить с помощью тригонометрического многочлена – отрезка ряда Фурье.
можно приблизить с помощью тригонометрического многочлена – отрезка ряда Фурье.
В утверждение, что функция ![]() хорошо приближает функцию
хорошо приближает функцию ![]() на компакте
на компакте ![]() , может быть вложен разный смысл. Например:
, может быть вложен разный смысл. Например:
а) можно потребовать, чтобы приближающая функция ![]() совпадала с
совпадала с ![]() в
в ![]() точках промежутка
точках промежутка ![]() , т.е. выполнялись условия
, т.е. выполнялись условия ![]() , для
, для ![]() .
.
Если ![]() - многочлен степени
- многочлен степени ![]() , то рассматриваемый процесс приближения называется параболическим интерполированием или процессом построения интерполяционного многочлена (частным примером является многочлен Лагранжа, т.е.
, то рассматриваемый процесс приближения называется параболическим интерполированием или процессом построения интерполяционного многочлена (частным примером является многочлен Лагранжа, т.е. ![]() );
);
б) функцию ![]() можно выбрать так, чтобы норма
можно выбрать так, чтобы норма ![]() - отклонения невязки – достигала минимального значения, причём норма может быть определена по-разному, и разным нормам соответствуют различные степени приближения.
- отклонения невязки – достигала минимального значения, причём норма может быть определена по-разному, и разным нормам соответствуют различные степени приближения.
В функциональном пространстве Гильберта ![]() , норме невязки имеет вид (интегральная норма Гаусса):
, норме невязки имеет вид (интегральная норма Гаусса):
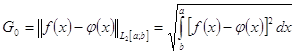 (4)
(4)
часто, в качестве нормы рассматривают Чебышевскую норму (Т – первая буква фамилии Чебышева на немецком языке):
![]() (5)
(5)
При использовании нормы (5) говорят о равномерном приближении функции ![]() , функцией
, функцией ![]() .
.
Подробная теория Т-приближений была развита в работах немецкого математика Л. Коллатца.
На практике, для оценки характера приближения, часто применяют метод наименьших квадратов, при котором невязка вычисляется по дискретной норме Гаусса:
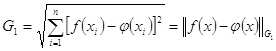 (6)
(6)
Ясно, что метод наименьших квадратов (6) – является дискретным аналогом функции Гаусса (4).
Принципиальную возможность приближения любой непрерывной функции ![]() многочленом даёт теорема Вейерштрасса: Если
многочленом даёт теорема Вейерштрасса: Если ![]() , тогда
, тогда ![]() ,
, ![]() - многочлен, что
- многочлен, что ![]() имеет место неравенство:
имеет место неравенство:
![]() (7)
(7)
2. Метод наименьших квадратов в случае приближения функции ![]()
Мы ранее рассматривали задачу аппроксимации результатов неточного эксперимента линейной функцией ![]() . Сейчас рассмотрим общий случай, когда функция
. Сейчас рассмотрим общий случай, когда функция ![]() приближается некоторой системой линейно независимых функций
приближается некоторой системой линейно независимых функций ![]() .
.
Как известно, для линейной независимости системы функций ![]() необходимо и достаточно, чтобы определитель Грама этой системы был отличен от нуля, т.е.
необходимо и достаточно, чтобы определитель Грама этой системы был отличен от нуля, т.е.
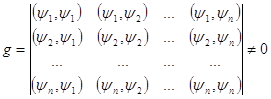 (8)
(8)
где ![]() означают скалярные произведения. Тогда для приближения (аппроксимации) функции
означают скалярные произведения. Тогда для приближения (аппроксимации) функции ![]() применяется линейная комбинация системы базисных функций, т.е.
применяется линейная комбинация системы базисных функций, т.е.
![]() (9)
(9)
В приближающей функции ![]() , неизвестными являются коэффициенты разложения
, неизвестными являются коэффициенты разложения ![]() , которые подбираются из условия минимума невязки, подсчитываемой по соответствующей норме. Вообще говоря,
, которые подбираются из условия минимума невязки, подсчитываемой по соответствующей норме. Вообще говоря, ![]() является элементом линейной оболочки, натянутой на систему базисных функций
является элементом линейной оболочки, натянутой на систему базисных функций ![]() .
.
2.1 Квадратичное приближение таблично заданной функции ![]() по дискретной норме Гаусса
по дискретной норме Гаусса
Рассмотрим задачу приближения функции ![]() в случае использования невязки в форме (6). Т.е. используем дискретную норму Гаусса:
в случае использования невязки в форме (6). Т.е. используем дискретную норму Гаусса:
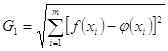 (10)
(10)
где неизвестная функция ![]() аппроксимируется функцией
аппроксимируется функцией ![]() из (9). Для
из (9). Для ![]() известны лишь значения в
известны лишь значения в ![]() различных точках
различных точках ![]() , т.е.
, т.е. ![]() , где
, где ![]() . Таким образом, для определения
. Таким образом, для определения ![]() имеем задачу: найти точку минимума
имеем задачу: найти точку минимума ![]() - невязки функции Гаусса
- невязки функции Гаусса ![]() - для таблично заданной функции
- для таблично заданной функции ![]() , если
, если
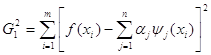 , (где
, (где ![]() ). (11)
). (11)
Очевидно, что условия минимума дискретной функции невязки Гаусса ![]() - имеют вид:
- имеют вид:
![]() ,
, ![]() (12)
(12)
Эти условия для (11) преобразуются к виду:
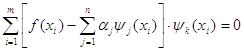 ,
, ![]() (13)
(13)
Раскрывая систему (13) получаем систему уравнений для определения коэффициентов разложения ![]() в виде:
в виде:
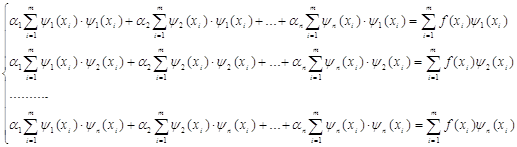 (14)
(14)
Нетрудно увидеть, что вводя скалярные произведения в соответствующем функциональном пространстве в виде:
![]() (15)
(15)
систему (14) можно переписать в нормальном виде Гаусса:
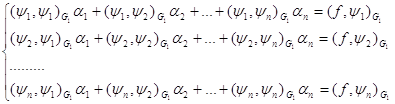 (16)
(16)
Ясно, что эта система имеет единственное решение, т.к. определитель системы (16) совпадает с определителем
Грама для базисных функций ![]() - которая отлична от нуля вследствие линейной независимости базисных функций.
- которая отлична от нуля вследствие линейной независимости базисных функций.
Найдя ![]() из системы (16) и подставляя в (9) мы получаем функцию:
из системы (16) и подставляя в (9) мы получаем функцию:
![]() (17)
(17)
которая является приближением к функции ![]() в смысле минимума квадратичного отклонения Гаусса (10) по норме индуцированной скалярным произведением (15), действительно:
в смысле минимума квадратичного отклонения Гаусса (10) по норме индуцированной скалярным произведением (15), действительно:
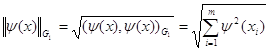 (18)
(18)
а дискретная норма Гаусса невязки имеет вид:
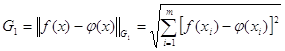 (19)
(19)
2.2 Интегральное приближение функции ![]() заданной аналитически
заданной аналитически
В предыдущем параграфе мы рассматривали приближение функции ![]() методом наименьших квадратов, предполагая, что значения функции
методом наименьших квадратов, предполагая, что значения функции ![]() заданы таблично, поэтому мы пользовались дискретной нормой Гаусса
заданы таблично, поэтому мы пользовались дискретной нормой Гаусса ![]() .
.
Рассмотрим теперь случай, когда аналитически заданную, на интервале ![]() , функцию
, функцию ![]() - надо аппроксимировать обобщённым многочленом:
- надо аппроксимировать обобщённым многочленом:
![]() (20)
(20)
так, чтобы минимизировалась интегральная норма невязки Гаусса ![]() :
:
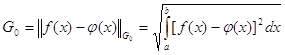 (21)
(21)
иначе говоря, нам нужно минимизировать интеграл
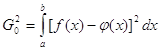 (22)
(22)
Для решения этой задачи подставим (20) в (22), тогда функционал (22) превратится в функцию многих переменных, т.е. ![]() . Условия же минимума функции многих переменных имеют вид:
. Условия же минимума функции многих переменных имеют вид:
![]() ,
, ![]() (23)
(23)
Эти условия приобретают вид:
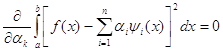 (24)
(24)
т.е.
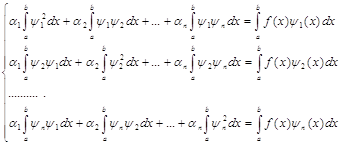 (25)
(25)
Определитель этой системы представляет собой определитель Грама для функций ![]() , в
, в ![]() , поэтому система (25) имеет единственное решение
, поэтому система (25) имеет единственное решение ![]() . Подставляя эти значения в разложение (20) имеем приближение для
. Подставляя эти значения в разложение (20) имеем приближение для ![]() . Характер приближения оценивается соответствующей нормой невязки
. Характер приближения оценивается соответствующей нормой невязки ![]() .
.
Задача аппроксимации функции заданной аналитически часто применяется для вычисления интегралов.
Похожие работы
... (19) где - матрица системы, - матрица правых частей, оценивается нормой: (20) Относительная погрешность оценивается по формуле: (21) где . 4. Итерационные методы решения систем линейных уравнений Рассмотрим систему линейных уравнений, которая плохо решается методами Гаусса. Перепишем систему уравнений в виде: ...
... f ¢(xо) = 0, >0 (<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные. На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b]. Пример 3.22. Найти экстремумы функции f(x) ...
... мероприятия по обеспечению однородности выпускаемой продукции. Все эти мероприятия можно объединить в четыре группы: 1. совершенствование технологии производства; 2. автоматизация производства; 3. технологические (тренировочные) прогоны; 4. статистическое регулирование качества продукции. 2.10. Проектирование технологических процессов с использованием средств ...
... мальне значення показникунадійності, при якому приймається рішення про орєінтованийзвязок назвем порогом показника надійності і позначимо (). Для можливості порівняння результатів у різних парах змінних в одній задачі системного синтезу корисно ввести відносний показник надійності. Відносним показником надійності ηij приняття рішення про напрям звязку між змінними xj → xi (стрілка в ...


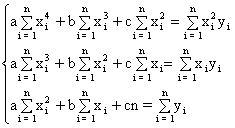


0 комментариев