Метод ортогонализации в случае несимметрической матрицы

1.2      Метод ортогонализации в случае несимметрической матрицы

В случае несимметрической матрицы процесс ортогонализации проводится точно также. Пусть векторы  уже построены. Тогда  ищется в виде

 (29)

Коэффициенты  определяются из системы

 (30)

Система в случае несимметрической матрицы будет треугольной.

Аналогично строится система «биортогональных» векторов, т.е. система 2n векторов, удовлетворяющих условию (12). При этом  – n произвольных линейно независимых векторов, а векторы  строятся последовательно в виде

 (31)

Коэффициенты  находятся из системы

 (32)

Также поступаем, отыскивая коэффициенты  и , при построении систем векторов (14) и (15), удовлетворяющих условиям (16).

При этом получим две системы:

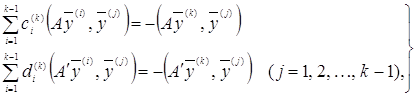 (33)

из которых и определяем  и .

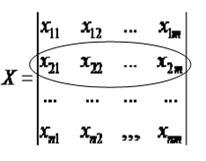
Остановимся еще на одном методе ортогонализации. Будем рассматривать строки матрицы А как векторы:

 (34)

Ортонормируем эту систему векторов. Первое уравнение системы  делим на . При этом получим

 (35)

где

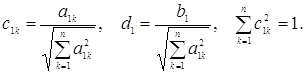 (36)

Второе уравнение системы заменится на

 (37)

где

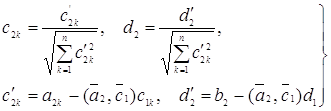 (38)

Аналогично поступаем дальше. Уравнение с номером i примет вид

 (39)

где

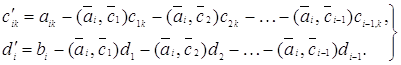 (40)

Процесс будет осуществим, если система уравнений линейно независима. В результате мы придем к новой системе , где матрица С будет ортогональной, т.е. обладает свойством СС¢=I.

Таким образом, решение системы можно записать в виде

. (41)

Практически, вследствие ошибок округления, СС¢ будет отлична от единичной матрицы и может оказаться целесообразным произвести несколько итераций для системы .

2.         Метод сопряженных градиентов

2.1 Первый алгоритм метода

Пусть требуется решить систему линейных алгебраических уравнений

(1)

с положительно определенной матрицей A порядка n.

Рассмотрим функционал

, (2)

представляющий многочлен второго порядка относительно x₁, x₂, …, x_n. Обозначим через  решение системы (1), т.е. . В силу симметричности и положительной определенности матрицы, имеем:

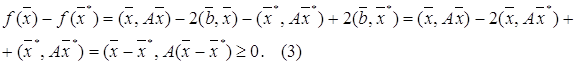
При этом знак равенства возможен лишь при . Таким образом, задача решения уравнения (1) сводится к задаче отыскания вектора , обращающего в минимум функционал (2).

Для отыскания такого вектора применим следующий метод.

Пусть  – произвольный начальный вектор, а

 (4)

– вектор невязок системы. Покажем, что вектор невязок  имеет направление нормали к поверхности в точке . В самом деле, направление нормали совпадает с направлением быстрейшего изменения функции  в точке . Это направление мы найдем, если найдем среди векторов , для которых , такой вектор, что

имеет наибольшее значение. Но

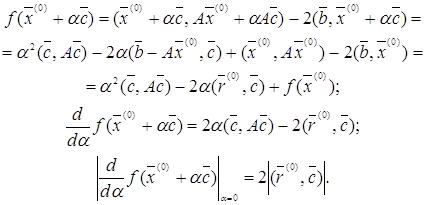
Но среди векторов  постоянный длины  достигает максимального значения, если  имеет направление вектора  или ему противоположное. Утверждение доказано. Будем двигаться из точки  в направлении вектора  до тех пор, пока функция  достигает минимального значения. Это будет при , т.е. при

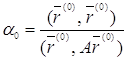. (5)

Вектор

 (6)

и принимаем за новое приближение к решению.

В методе сопряженных градиентов следующее приближение  находится так. Через точку  проведем гиперплоскость (n-1) – го измерения

 (7)

и через  обозначим новую невязку системы

. (8)

Вектор  направлен по нормали к поверхности  в точке , а вектор  параллелен касательной плоскости в этой точке. Поэтому

. (9)

Гиперплоскость (7) проходит через точку , так как

.

При любом  вектор  параллелен некоторой нормальной плоскости к поверхности  в точке . Найдем среди них тот, который лежит в гиперплоскости (7), т.е. ортогонален к . Из условия ортогональности имеем:

,

или

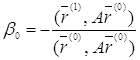. (10)

Вектор

 (11)

имеет направление нормали к сечению поверхности  гиперплоскости (7) в точке . Будем двигаться из точки  в направлении вектора  до тех пор, пока функция  достигнет минимума. Это будет при

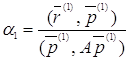. (12)

Вектор

примем за новое приближение к решению  системы. Вектор невязок

 (13)

имеет направление нормали к поверхности  в точке . Покажем, что он будет ортогонален к  и . В самом деле, используя (9), (11), (12), (13), имеем:

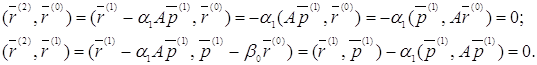
Рассмотрим гиперплоскость (n-2) – х измерений

, (14)

проходящую через точку . Эта гиперплоскость содержит и , так как мы ранее видели, что , а

.

Вектор  при любом  параллелен гиперплоскости (7), так как

.

Подберем  так, чтобы он был параллелен и гиперплоскости (14), т.е. потребуем ортогональности к вектору . Будем иметь:

,

или

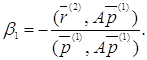 (15)

Вектор

 (16)

будет иметь направление нормали к сечению поверхности гиперплоскостью (14) в точке . Из точки  сместимся в направлении этого вектора так, чтобы функция  достигла минимального значения. Это будет при

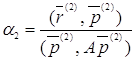, (17)

 (18)

примем за новое приближение к . Новый вектор невязок будет:

. (19)

Продолжая процесс, получим последовательности векторов , , , определяемые рекуррентными соотношениями:

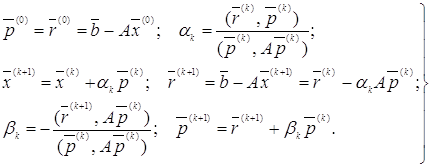 (20)

Для этих векторов имеют место следующие соотношения:

 (21)

 (22)

В самом деле, в силу самого построения при i¹j

Далее, при i>j

Если i=j+1, то правая часть равна нулю, в силу определения , если же i>j+1, то , по доказанному, и

.

Продолжая понижение индекса у вектора , через несколько шагов придем к скалярному произведению  (по определению ). Таким образом, соотношения (21) доказаны. Для доказательства (22), в силу равноправия индексов i и j, предположим, что i>j. Тогда

.

Так как в n-мерном векторном пространства не может быть более n взаимно ортогональных векторов, то на некотором шаге  получим , т.е.  будет решением системы (1).

На рис. 1 показана геометрическая картина нашего построения при n=3.

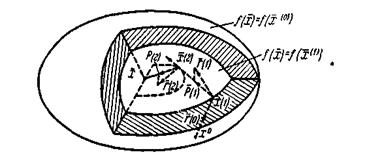
Рис. 1