Второй алгоритм метода

2.2 Второй алгоритм метода

Приведем другой алгоритм метода. Будем обозначать последовательные приближения к решению через  и введем обозначения:

. (23)

Первые два приближения  и  возьмем так, чтобы

. (24)

Предположим, что уже известно приближение  (i³1), вычислены  и справедливо равенство

. (25)

Будем искать минимум функционала (2) на множестве векторов

. (26)

Приравнивая к нулю частные производные от  по  и  для определения  и , получим систему:

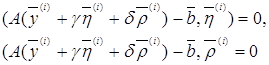 (27)

или, учитывая (25),

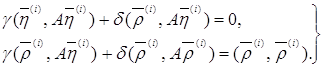 (28)

Обозначим через  решение этой системы:

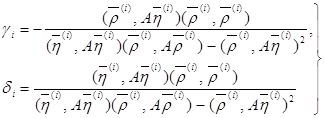 (29)

и за (i+1) – е приближение к решению примем:

 (30)

Из системы (27) следует, что

, (31)

а так как

то из (31) следует:

 (32)

Докажем, что если

 (33)

то при всех i

 (34)

что будет доказывать и сходимость, и конечность второго алгоритма.

В самом деле, при условиях (33)

и

т.е. условие (24) выполнено. Предположим, что уже доказаны равенства

 (35)

и докажем равенство

При предположении (35)  и, следовательно,

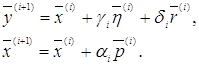
Но из соотношений (20) имеем:

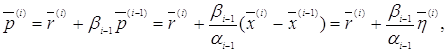
т.е.

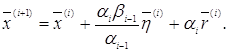
Докажем коллинеарность векторов

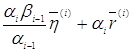 и  (36)

Из (20) и (29) имеем:

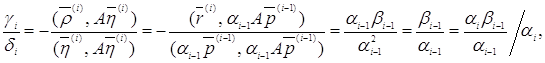
а это и доказывает коллинеарность векторов (36).

Вектор  дает минимум функционала в плоскости, проходящей через  и натянутой на векторы  и , а мы показали, что этот минимум лежит на прямой, проходящей через  в направлении вектора . Но на этой прямой минимум функционала достигается на векторе . Это и означает, что

Это и доказывает справедливость (34) при всех i.

На первый взгляд кажется, что первый алгоритм лучше, так как на каждом шаге он требует лишь одного умножения матрицы А на вектор , а во втором алгоритме требуется два умножения матрицы А на вектор  и , но опыт показал, что применение первого алгоритма приводит к быстрому накоплению ошибок округления, так что для матриц большого порядка возможно существенное отклонение от точного решения. Второй алгоритм менее чувствителен к ошибкам округления и поэтому требует меньшего количество шагов для получения хорошего приближенного решения.

Метод сопряженных градиентов целесообразно использовать для решения систем уравнений, в которых матрица А имеет много нулевых элементов. При решении системы по этому методу элементы матрицы участвуют в арифметических операциях лишь при умножении матрицы на вектор, а умножение матрицы на вектор можно организовать так, чтобы в арифметических операциях участвовали только ненулевые элементы.

Заключение

В данной работе были рассмотрены метод ортогонализации и метод сопряженных градиентов, а также представлена программа на языке программирования С++, реализующая метод ортогонализации на ЭВМ, и ее результаты работы.

Список литературы

1. Березин И.С. и Жидков Н.П. Методы вычислений. т. 1. М.: «Наука», 1965. 633c.

2. Воеводин В.В. Численные методы алгебры (теория и алгоритмы). М.: «Наука», 1966.

3. Подбельский В.В. и Фомин С.С. Программирование на языке Си. М.: «Финансы и статистика», 2000. 599 с.

4. Калиткин Н.Н. Численные методы. М.: «Наука», 1978. 512 с.