Обзор научно-технической литературы
Линейное программирование
Целочисленное линейное программирование - метод ветвей и границ
Алгоритм
Решение задач оптимизации при помощи средства «Поиск решения» в Microsoft Excel
Постановка задачи планирования производства в общем случае
Решение поставленной задачи планирования производства
Проверка признака допустимости и оптимальности базиса
Схема программы
Навигация
Обзор научно-технической литературы
Решения задачи планирования производства симплекс методом
82416
знаков
8
таблиц
19
изображений
1. Обзор научно-технической литературы
1.1 История развития экономико-математического планирования
В 1938-1939 гг. ленинградский математик (впоследствии академик, лауреат Ленинской, Государственных и Нобелевской премий) Л.В. Канторович в результате анализа ряда проблем организации и планирования производства сформулировал новый класс условно-экстремальных задач и предложил методы их решения. Так было положено начало новой отрасли прикладной математики линейному программированию. В более поздних работах Л. В. Канторович расширил область применения линейного программирования в социалистической экономике, сформулировав задачи отраслевого и народнохозяйственного оптимального планирования. А через два десятилетия после своего возникновения линейное программирование стало основным инструментом плановоэкономических решений на всех уровнях социалистического народного хозяйства.
В том же 1939 г. ленинградский экономист В. В. Новожилов, рассматривая эффективность плановых и проектных решений, сформулировал важные теоретические положения, ставшие потом органической частью теории оптимального планирования социалистической экономики.
Далее методы планирования продолжали совершенствоваться, но только развитие вычислительной техники в конце 50-х гг. позволило сделать плановые многовариантные расчеты достаточно распространенными. Важную роль в организации и пропаганде экономико-математических исследований в этот период сыграл академик В. С. Немчинов. Именно в эти годы получают развитие некоторые разделы прикладной математики, связанные с решением оптимизационных задач: линейное и нелинейное программирование, теория оптимального управления и др. В 60-е гг. основное внимание исследователей сосредоточивается на разработке оптимизационных моделей различных типов и их практическом применении к решению задач планирования. Было построено большое количество экономико-математических моделей, на основе которых проведены расчеты по составлению реальных оптимальных планов (оптимальные планы перевозок, эксплуатации подвижного состава транспорта, использования топлива, загрузки оборудования предприятий; оптимальное размещение отдельных отраслей промышленности и предприятий отрасли; оптимальное планирование и распределение капиталовложений и т. д.), что дало большой народнохозяйственный эффект. Наряду с расширением сферы применения математических моделей в экономике и планировании осуществляется процесс усовершенствования моделей и использования более адекватного математического аппарата: переход от статических моделей к динамическим, от жестко детерминированных к стохастическим моделям, учитывающим случайность и неопределенность экономических процессов, применение дискретного программирования, методов статистического моделирования, создание новых алгоритмов, позволяющих решать задачи большой размерности.
1.2 Необходимость решения задач линейного программирования
Применение экономико-математических методов и моделей позволяет существенно улучшить качество планирования и получить дополнительный экономический эффект без вовлечения в общественное производство дополнительных ресурсов, что чрезвычайно важно в условиях перехода экономики на преимущественно интенсивный путь развития.
В настоящее время область возможного применения экономико-математических методов в планировании чрезвычайно велика и с каждым годом она расширяется. Однако область фактического их применения в практике плановых расчетов намного скромнее. Это объясняется трудностями широкого внедрения экономико-математических методов.
К числу их следует отнести: сложность определения критерия оптимальности в ряде экономических задач; трудности при решении проблемы «встраивания» математических моделей в существующую систему планирования и управления, приводящие к необходимости создания новой технологии планирования, базирующегося на системном использовании экономико-математических методов и ЭВМ; стохастический и динамический характер экономических процессов, требующий усложнения используемого математического аппарата и программного обеспечения ЭВМ, увеличения объема вычислений; трудность измерений многих экономических явлений и получения массовой достоверной информации для наполнения разработанных моделей; трудность проверки правильности (верификации) экономикоматематических моделей, ориентированных не столько на подтверждение действительности, сколько на решение новых социально-экономических задач (это в первую очередь относится к моделям планирования и прогнозирования), и т. д.
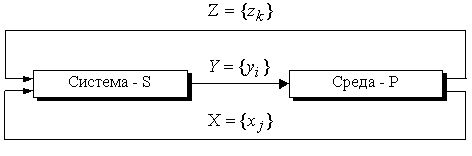
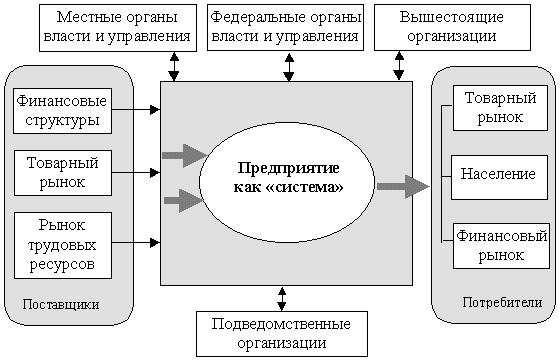
Но главная трудность заключается в сложности моделируемых экономических процессов и явлений. Большинство объектов, изучаемых экономической наукой, может быть охарактеризовано кибернетическим понятием «сложная система». При изучении систем недостаточно (а иногда и невозможно) пользоваться методом расчленения на элементы с последующим изучением этих элементов в отдельности.
Кроме того, моделирование существенно усложняется тем, что экономика охватывает не только производственные процессы, но и производственные отношения. Моделировать производственные отношения невозможно, не учитывая поведение людей, их интересы и индивидуально принятые решения.
В результате производственно-хозяйственная или социально-экономическая ситуация, в которой приходится принимать плановые решения, часто оказывается намного богаче и сложнее тех моделей, которые используются в планировании в этой ситуации.
В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решений, в том числе и в финансовой математике. Для решения задач линейного программирования разработано сложное программное обеспечение, дающее возможность эффективно и надежно решать практические задачи больших объемов. Эти программы и системы снабжены развитыми системами подготовки исходных данных, средствами их анализа и представления полученных результатов. В развитие и совершенствование этих систем вложен труд и талант многих математиков, аккумулирован опыт решения тысяч задач. Владение аппаратом линейного программирования необходимо каждому специалисту в области прикладной математики.
Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи:
рационального использования сырья и материалов; задачи оптимального раскроя;
оптимизации производственной программы предприятий;
оптимального размещения и концентрации производства;
составления оптимального плана перевозок, работы транспорта;
управления производственными запасами;
и многие другие, принадлежащие сфере оптимального планирования.
Для большого количества практически интересных задач целевая функция выражается линейно – через характеристики плана, причем допустимые значения параметров подчинены линейным равенствам или неравенствам. Нахождение при данных условиях абсолютного экстремума целевой функции носит название линейного программирования.
Первым исследованием по линейному программированию является работа Л. В. Канторовича “Математические методы организации и планирования производства”, опубликованная в 1939 г. В нем дана постановка задач линейного программирования, разработан метод разрешающих множителей решения задач линейного программирования и дано его теоретическое обоснование.
Прямая задача линейного программирования является математической формулировкой проблемы составления такого плана использования различных способов производства, который позволяет получить максимальное количество однородного продукта при имеющихся в наличии ресурсах.
Математическое программирование – это прикладная отрасль математики, которая является теоретической основой решения задач оптимального планирования.
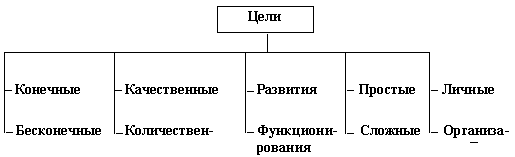
Существуют следующие разделы математического программирования: линейное, параметрическое, нелинейное и динамическое программирование. Наиболее разработанным и широко применяемым разделом математического программирования является линейное программирование, целью которого служит отыскивание оптимума (max, min) заданной линейной функции при наличии ограничений в виде линейных уравнений или неравенств.
Похожие работы
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
... определение базисных решений соответст- вует идентификации экстремальных точек , осуществляемой при геометрическом представлении пространства решений . Таким об- разом , максимальное число итераций при использовании симплекс- метода равно максимальному числу базисных решений задачи ЛП , представленной в стандартной форме . Это означает , что количество итерационных процедур симплекс-метода не ...
... - метод для решения задач линейного программирования. Задачи курсовой заботы: 1. привести теоретический материал; 2. на примерах рассмотреть симплекс метод; 3. представить данную курсовую работу в виде презентации. Математическое программирование Математическое программирование занимается изучение экстремальных задач и поиском методов их решения. Задачи ...
... предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, еще до того, как компьютеры были использованы для решения линейных задач оптимизации. Формулировка задачи линейного программирования Нужно максимизировать при условиях при i = 1, 2, 3, . . ., m.. Иногда на xi также накладывается некоторый набор ограничений в виде равенств, но от ...
0 комментариев