Навигация
Проверка признака допустимости и оптимальности базиса
3.3.4 Проверка признака допустимости и оптимальности базиса
Признак допустимости базиса:
в опорной точке в соответствии с (7) xj=bi, i=6,…,10; j=6,…,10, поэтому признак допустимости базиса формулируется как условие bi![]() 0, i=6,…,10.
0, i=6,…,10.
Признак оптимальности базиса:
Если для ![]() то найденное решение оптимально и единственно.
то найденное решение оптимально и единственно.
Если для ![]() то найденное решение оптимально, но не единственно.
то найденное решение оптимально, но не единственно.
Если ![]() то решение неоптимально. В этом случае поиск оптимального решения продолжается и необходимо перейти к новой опорной точке.
то решение неоптимально. В этом случае поиск оптимального решения продолжается и необходимо перейти к новой опорной точке.
Перейдем к конкретному случаю. В нашем случае выполняется условие допустимости базиса, так как b=(600, 590, 750, 670, 495)T<0 и bi<0 (i=6,…,10).
Выбранный нами начальный базис XБО=(x6, x7, x8, x9, x10)T не является оптимальным, так как c1=-60<0, c2=-50<0, c3=-37<0, c4=-45<0 и c6=56<0. Таким образом, необходимо осуществить переход к новой опорной точке (новому базису).
3.3.5 Нахождение разрешающего элемента в симплекс-таблице. Формирование нового базиса
В соответствии с симплекс-методом новая опорная точка выбирается только среди соседних, то есть новый базис лишь одной переменной отличается от прежнего. Таким образом, формирование нового базиса осуществляется на базе прежнего посредством выведения из него одной из базисных переменных xs и введения одной из свободных переменных xr.
Выбор переменной xr. Выбор переменной xr осуществляется по результатам анализа коэффициентов cj симплекс-таблицы. Найдем cr=![]() .
.
В нашем случае min{c1, c2, c3, c4, c5}=c1=-60 и xr=x1.
Столбец, который соответствует переменной xr=x1 в симплекс-таблице, будем называть разрешающим.
Выбор переменной xs. Выбор переменной xs проводится по результатам анализа коэффициентов air i=1,2,3,4,5 разрешающего столбца.
Если ![]() , это означает, что ОДР такова, что неограниченное увеличение свободной переменной xr приводит к неограниченному возрастанию целевой функции (ОДР не замкнута).
, это означает, что ОДР такова, что неограниченное увеличение свободной переменной xr приводит к неограниченному возрастанию целевой функции (ОДР не замкнута).
Если ![]() , то соответствующие базисные переменные xi (i=6,7,8,9,10) получают отрицательные приращения при увеличении xr=x1. Среди этих переменных xi необходимо отыскать xs, достигающую нуля при минимальном значении приращения xr. Нужно найти
, то соответствующие базисные переменные xi (i=6,7,8,9,10) получают отрицательные приращения при увеличении xr=x1. Среди этих переменных xi необходимо отыскать xs, достигающую нуля при минимальном значении приращения xr. Нужно найти
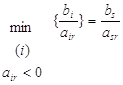 .
.
В нашем случае min{600/1, 590/2, 750/4, 670/3, 495/1}=min{600,295,187.5,223.3,495}=187.5 и xs=x8. Строка, которая соответствует переменной xs=x8 в симплекс-таблице, называется разрешающей. Элемент asr=a81=4 называется разрешающим элементом симплекс-таблицы.
Выбор разрешающего элемента завершает формирование нового базиса XБ1, отличающегося от прежнего базиса одной переменной xr=x1, то есть вместо переменной x8 в базис XБ1 будет включена переменная x1: XБ1=(x6, x7, x1, x9, x10)T.
Для нового базиса (новой опорной точки) снова заполняется симплекс-таблица, в которой новые базисные переменные выражены через новые свободные.
3.3.6 Пересчет симплекс-таблицы
Правила пересчета:
Разрешающий элемент заменяется на 1.
Элементы разрешающего столбца за исключением asr переписываются без изменений.
Элементы разрешающей строки за исключением asr изменяют знак на противоположный.
Оставшиеся элементы новой симплекс-таблицы вычисляются согласно следующему правилу: произведение соответствующего элемента прежней таблицы на разрешающий элемент asr минус произведение элементов, находящихся на другой диагонали таблицы. В соответствии с этим правилом имеем:
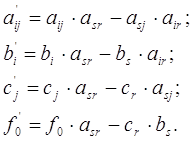
Все элементы полученной таблицы необходимо разделить на разрешающий элемент asr:
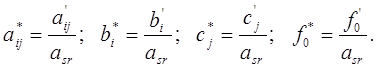
Таблица 3. Итерация №1
| БП | СЧ | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 |
| X6 | 825/2 | 0 | 15/4 | 5/4 | 3/4 | 5/2 | 1 | 0 | -1/4 | 0 | 0 |
| X7 | 215 | 0 | 3/2 | -1/2 | 7/2 | 1 | 0 | 1 | -1/2 | 0 | 0 |
| X1 | 375/2 | 1 | 1/4 | 3/4 | 1/4 | 1/2 | 0 | 0 | 1/4 | 0 | 0 |
| X9 | 215/2 | 0 | 5/4 | 7/4 | 5/4 | -1/2 | 0 | 0 | -3/4 | 1 | 0 |
| X10 | 615/2 | 0 | 7/4 | 1/4 | 15/4 | 7/2 | 0 | 0 | -1/4 | 0 | 1 |
| Y | 11250 | 0 | -35 | 8 | -30 | -26 | 0 | 0 | 15 | 0 | 0 |
XБ1=(x6, x7, x1, x9, x10)T.
Базис XБ1=(x6, x7, x1, x9, x10)T является допустимым, но не оптимальным. Разрешающий элемент таблицы a92=5/4 определяет необходимость перехода к базису XБ2=(x6, x7, x1, x2, x10)T. Приведем результат пересчета симплекс-таблицы для базиса XБ2.
Таблица 4. Итерация №2.
| БП | СЧ | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 |
| X6 | 90 | 0 | 0 | -4 | -3 | 4 | 1 | 0 | 2 | -3 | 0 |
| X7 | 86 | 0 | 0 | -13/5 | 2 | 8/5 | 0 | 1 | 2/5 | -6/5 | 0 |
| X1 | 166 | 1 | 0 | 2/5 | 0 | 3/5 | 0 | 0 | 2/5 | -1/5 | 0 |
| X2 | 86 | 0 | 1 | 7/5 | 1 | -2/5 | 0 | 0 | -3/5 | 4/5 | 0 |
| X10 | 157 | 0 | 0 | -11/5 | 2 | 21/5 | 0 | 0 | 4/5 | -7/5 | 1 |
| Y | 14260 | 0 | 0 | 57 | 5 | -40 | 0 | 0 | -6 | 28 | 0 |
Базис XБ2=(x6, x7, x1, x2, x10)T является допустимым, но не оптимальным. Разрешающий элемент таблицы a65=4 определяет необходимость перехода к базису XБ3=( x5, x7, x1, x2, x10)T. Приведем результат пересчета симплекс-таблицы для базиса XБ3.
Таблица 5. Итерация №3
| БП | СЧ | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 |
| X5 | 45/2 | 0 | 0 | -1 | -3/4 | 1 | 1/4 | 0 | 1/2 | -3/4 | 0 |
| X7 | 50 | 0 | 0 | -1 | 16/5 | 0 | -2/5 | 1 | -2/5 | 0 | 0 |
| X1 | 305/2 | 1 | 0 | 1 | 9/20 | 0 | -3/20 | 0 | 1/10 | 1/4 | 0 |
| X2 | 95 | 0 | 1 | 1 | 7/10 | 0 | 1/10 | 0 | -2/5 | 1/2 | 0 |
| X10 | 125/2 | 0 | 0 | 2 | 103/20 | 0 | -21/20 | 0 | -13/10 | 7/4 | 1 |
| Y | 15160 | 0 | 0 | 17 | -25 | 0 | 10 | 0 | 14 | -2 | 0 |
Базис XБ3=(x5, x7, x1, x2, x10)T является допустимым, но не оптимальным. Разрешающий элемент таблицы a104=103/20 определяет необходимость перехода к базису XБ4=(x5, x7, x1, x2, x4)T. Приведем результат пересчета симплекс-таблицы для базиса XБ4.
Таблица 6. Итерация №4
| БП | СЧ | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 |
| X5 | 3255/103 | 0 | 0 | -73/103 | 0 | 1 | 10/103 | 0 | 32/103 | -51/103 | 15/103 |
| X7 | 1150/103 | 0 | 0 | -231/103 | 0 | 0 | 26/103 | 1 | 42/103 | -112/103 | -64/103 |
| X1 | 15145/103 | 1 | 0 | 85/103 | 0 | 0 | -6/103 | 0 | 22/103 | 10/103 | -9/103 |
| X2 | 8910/103 | 0 | 1 | 75/103 | 0 | 0 | 25/103 | 0 | -23/103 | 27/103 | -14/103 |
| X4 | 1250/103 | 0 | 0 | 40/103 | 1 | 0 | -21/103 | 0 | -26/103 | 35/103 | 20/103 |
| Y | 15463,4 | 0 | 0 | 2751/103 | 0 | 0 | 505/103 | 0 | 792/103 | 669/103 | 500/103 |
Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T.
3.4 Результат решения задачи планирования производства
В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем наложенным ограничениям и обеспечивает максимальную стоимость данного набора (максимум целевой функции f(x)= 60x1+50x2+37x3+45x4+56x5=15463,4 рублей). Таким образом, можно оптимально спланировать объем производства продукции при наличии заданного количества ресурсов: продукции типа A нужно выпустить 147 единиц, продукции типа B – 86 единиц, продукции типа D – 12 единиц, продукции типа E – 31 единицу, а продукцию типа D – для достижения максимальной прибыли в данных условиях производить не выгодно.
При этом ресурсы типа 1, 3, 4, 5 будут использованы полностью, а 11 единиц ресурса типа 2 останутся неизрасходованными.
4. Программа для решения задач ЛП симплекс методом
4.1 Описание
В процессе выполнения дипломной работы был реализован и отлажен программный интерфейс под ОС Windows XP (также протестирован под Windows Vista), решающий задачи ЛП симплекс методом (в частности поставленную задачу планирования производства).
Программа осуществляет: решение задач ЛП симплекс методом; сохранение и загрузка исходных данных в файл/из файла; вывод решения по шагам; экспорт решения в документ MS word; системный код программы написан в среде объектно-ориентированного программирования С++.
4.2 Графическое представление программы
Главное окно программы «Исходные данные»:
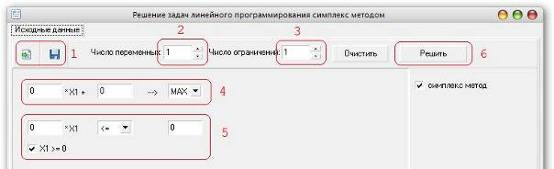
Рис.5 Главное окно программы Simplex: 1 – Кнопки загрузка/сохранение исходных данных в файл. 2 – Число переменных, в нашем случае количество производимой продукции. 3 – Число ограничений, в нашем случае количество запасов ресурсов на складе. 4 – Целевая функция, в нашем случае максимизация. 5 – Система ограничений в форме Такера. 6 – Кнопка для решения задачи и перехода к окну «Решение».
Окно программы «Решение»:
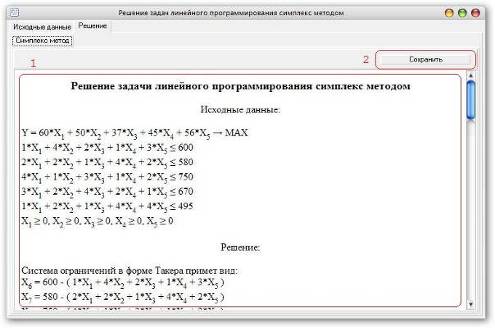
Рис.6 Окно программы Simplex, для просмотра решения по шагам: 1 – Поле для вывода пошагового решения задачи. 2 – Кнопка для экспорта результатов работы программы в документ MS Word.
4.3 Работа с программой
1 – Определяем число переменных; 2 – Определяем максимизируем или минимизируем целевую функцию; (см. Рис.7)
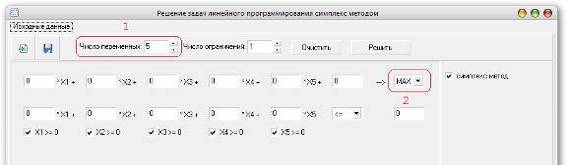
Рис.7 Работа с программой
3 – Определяем число ограничений; 4 – Определяем знаки неравенств для системы ограничений; 5 – Указываем дополнительные ограничения неотрицательности; (см. Рис.8)
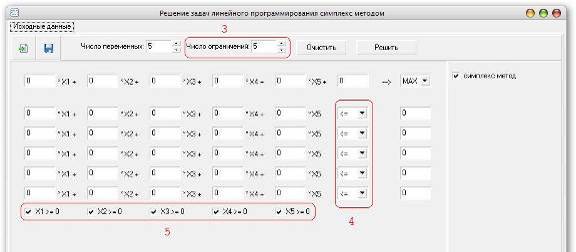
Рис.8 Работа с программой
Приступаем к вводу исходных данных: 6 – поля для ввода коэффициентов целевой функции (в нашем случае это цена единицы продукции типа A,…,E); 7 – поля для ввода запасов каждого ресурса; 8 – поля для ввода набора производимой продукции. Заполнив все поля, приступаем к решению задачи: 9 – нажимаем кнопку «Решить». (см. Рис.9)
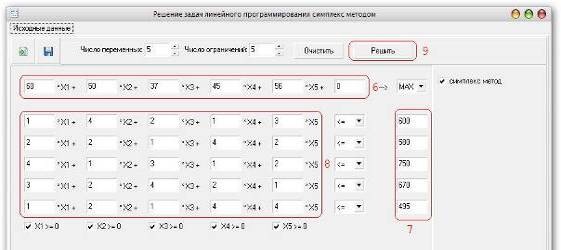
Рис.9 Работа с программой
После нажатия кнопки «Решения» программа производит необходимые вычисления и автоматически переходит ко второму окну, в котором отображается пошаговое решение поставленной задачи в виде симплекс таблиц, с указанием необходимых дополнительных данных. А именно: 10 - исходные данные; 11 - система ограничений в форме Такера; 12 - целевая функция; 13 – исходная симплекс таблица; (см. Рис.10)
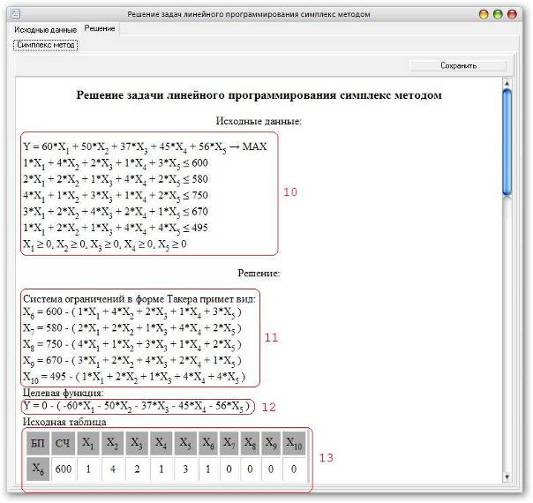
Рис.10 Работа с программой
14 - разрешающий элемент каждой таблицы, 15 - переход от старого базиса к новому, 16 - количество итераций, 17 - информация об оптимальности решения, 18 – Ответ, в нашем случае максимум целевой функции (максимальная прибыль), 19 – оптимальный набор производимой продукции (количество изделий A,…,E). (см. Рис.11)
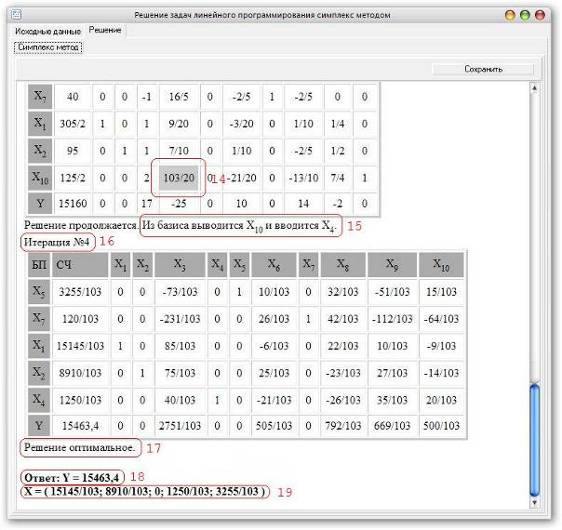
Рис.11 Работа с программой
Похожие работы
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
... определение базисных решений соответст- вует идентификации экстремальных точек , осуществляемой при геометрическом представлении пространства решений . Таким об- разом , максимальное число итераций при использовании симплекс- метода равно максимальному числу базисных решений задачи ЛП , представленной в стандартной форме . Это означает , что количество итерационных процедур симплекс-метода не ...
... - метод для решения задач линейного программирования. Задачи курсовой заботы: 1. привести теоретический материал; 2. на примерах рассмотреть симплекс метод; 3. представить данную курсовую работу в виде презентации. Математическое программирование Математическое программирование занимается изучение экстремальных задач и поиском методов их решения. Задачи ...
... предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, еще до того, как компьютеры были использованы для решения линейных задач оптимизации. Формулировка задачи линейного программирования Нужно максимизировать при условиях при i = 1, 2, 3, . . ., m.. Иногда на xi также накладывается некоторый набор ограничений в виде равенств, но от ...


0 комментариев