Навигация
Решение поставленной задачи планирования производства
3.3 Решение поставленной задачи планирования производства
Описание метода решения задачи.
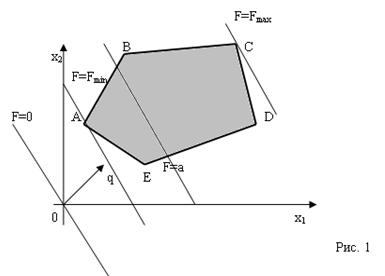
Процедура решения ЗЛП начинается с приведения ее к канонической форме, то есть к стандартной форме задания, ориентированной на разработанный именно для этой формы метод решения. Задача линейного программирования в канонической форме имеет смысл при условии n>m. В этом случае полностью описывается область допустимых решений (ОДР) ЗЛП, геометрически являющуюся выпуклым многогранником в евклидовом пространстве Rn[1]. Выпуклая фигура, как известно, характеризуется тем свойством, что, если две точки X1 и X2 принадлежат этой фигуре, то и весь отрезок X1X2 принадлежит ей. Кроме того, доказано, что оптимальное решение ЗЛП всегда лежит на границе ОДР. Поэтому справедлив вывод о том, что, по крайней мере, одна из угловых (опорных) точек выпуклого многогранника ОДР является точкой оптимума. Для того, чтобы определить координаты опорной точки, все множество переменных X={xj}, j=![]() необходимо разделить на два подмножества
необходимо разделить на два подмножества
![]() :
:
подмножество базисных переменных ![]() , при этом число m базисных переменных равно числу уравнений (ограничивается) при условии, что уравнения являются линейно-независимыми; подмножество
, при этом число m базисных переменных равно числу уравнений (ограничивается) при условии, что уравнения являются линейно-независимыми; подмножество ![]() остальных n-m свободных (внебазисных) переменных {xj}, j
остальных n-m свободных (внебазисных) переменных {xj}, j![]() Б[1].
Б[1].
Количество возможных вариантов разделения переменных на базисные и свободные (число базисов) равно ![]() .
.
Наиболее очевидный метод решения ЗЛП состоит в том, чтобы для каждого из ![]() базисов найти координаты соответствующих опорных точек, выделить из них точки, принадлежащие ОДР, а затем из них, в свою очередь, выбрать ту, координаты которой максимизируют целевую функцию. В отличие от этого метода, реализующего, по сути, идею полного перебора опорных точек ОДР, известен более эффективный так называемый симплекс-метод решения ЗЛП.
базисов найти координаты соответствующих опорных точек, выделить из них точки, принадлежащие ОДР, а затем из них, в свою очередь, выбрать ту, координаты которой максимизируют целевую функцию. В отличие от этого метода, реализующего, по сути, идею полного перебора опорных точек ОДР, известен более эффективный так называемый симплекс-метод решения ЗЛП.
В основе симплекс-метода лежит подход, включающий:
выбор опорной точки, принадлежащей ОДР (выбор начального допустимого базиса);
проверку опорной точки на оптимальность;
выбор нового базиса, позволяющего минимизировать число опорных точек на траектории в случае невыполнения условий оптимальности.
Приведение исходной задачи к каноническому виду.
Имеем исходную ЗЛП:
{60x1+50x2+37x3+45x4+56x5}![]() max.
max.
x1+4x2+2x3+x4+3x5![]() 600;
600;
2x1+2x2+x3+4x4+2x5![]() 590;
590;
4x1+x2+3x3+x4+2x5![]() 750;(4)
750;(4)
3x1+2x2+4x3+2x4+x5![]() 670;
670;
x1+2x2+x3+4x4+4x5![]() 495;
495;
x1, x2, x3, x4, x5 ![]() 0.
0.
Приведем ЗЛП к канонической форме. Приведение системы ограничений, заданных в форме неравенств, к канонической форме равенств осуществляется посредством соответствующего увеличения размерности вектора X=(x1, x2, x3, x4, x5) с учетом обязательной неотрицательности всех его составляющих.
Таким образом, ЗЛП в канонической форме имеет вид:
max {60x1+50x2+37x3+45x4+56x5};
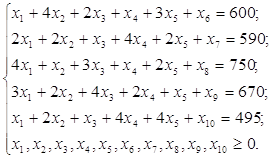 (5)
(5)
Поиск допустимого базиса.
Заполнение симплекс-таблицы.
ЗЛП в канонической форме можно записать в матричном виде:
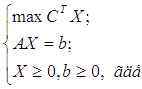 (6)
(6)
b=(600, 590, 750, 670, 495)T,
X=(x1, x2, x3, x4, x5, x6, x7, x8, x9, x10)T,
C=(60,50,37,45,56,0,0,0,0,0),
A=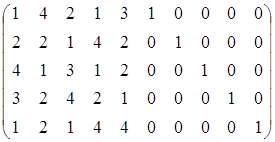 .
.
Поиск допустимого базиса начинается с анализа столбцов матрицы A=(A1, A2,…, A10), используемой в записи ограничения (6) канонической формы ЗЛП. В качестве базисных следует выбирать такие 5 переменных, которым соответствует набор столбцов, позволяющих составить единичную матрицу P=(Aj1, Aj2, Aj3, Aj4, Aj5).
Если ОДР исходной ЗЛП задана в форме неравенств типа ![]() (как в нашем случае), то начальный базис может быть сформирован из дополнительных переменных x6, x7, x8, x9, x10, вводимых в систему ограничений с целью приведения ее к канонической форме равенств. В этом случае матрица P будет единичной.
(как в нашем случае), то начальный базис может быть сформирован из дополнительных переменных x6, x7, x8, x9, x10, вводимых в систему ограничений с целью приведения ее к канонической форме равенств. В этом случае матрица P будет единичной.
Таким образом, выберем в качестве начального базиса XБО=(x6, x7, x8, x9, x10)T, так как столбцы A6, A7, A8, A9, A10 матрицы A образуют единичную матрицу.
Теперь перейдем к заполнению симплекс-таблицы. Пусть ЗЛП сформулирована в канонической форме (5). Мы выбрали базисные переменные x6, x7, x8, x9, x10. Разрешим систему неравенств в (5) относительно базисных переменных.
Система ограничений в форме Такера примет вид:
x6=600-(x1+4x2+2x3+x4+3x5);
x7=590-(2x1+2x2+x3+4x4+2x5);
x8=750-(4x1+x2+3x3+x4+2x5);(7)
x9=670-(3x1+2x2+4x3+2x4+x5);
x10=495-(x1+2x2+x3+4x4+4x5);
Целевую функцию можно представить в виде:
f(x)=f0-(-60x1-50x2-37x3-45x4-56x5), где f0=0.
Симплекс-таблица выглядит следующим образом:
Таблица 1. Исходная симплекс таблица в общем виде
| b | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | |
| x6 | b6 | a61 | a62 | a63 | a64 | a65 | a66 | a67 | a68 | a69 | a610 |
| x7 | b7 | a71 | a71 | a71 | a71 | a71 | a71 | a71 | a71 | a71 | a710 |
| x8 | b8 | a81 | a82 | a83 | a84 | a85 | a86 | a87 | a88 | a89 | a810 |
| x9 | b9 | a91 | a92 | a93 | a94 | a95 | a96 | a97 | a98 | a99 | a910 |
| x10 | b10 | a101 | a102 | a103 | a104 | a105 | a106 | a107 | a108 | a109 | a1010 |
| f(x) | f0 | c1 | c2 | c3 | c4 | c5 | c6 | c7 | c8 | c9 | c10 |
В нашем случае:
Таблица 2. Исходная симплекс таблица поставленной задачи
| БП | СЧ | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 |
| X6 | 600 | 1 | 4 | 2 | 1 | 3 | 1 | 0 | 0 | 0 | 0 |
| X7 | 590 | 2 | 2 | 1 | 4 | 2 | 0 | 1 | 0 | 0 | 0 |
| X8 | 750 | 4 | 1 | 3 | 1 | 2 | 0 | 0 | 1 | 0 | 0 |
| X9 | 670 | 3 | 2 | 4 | 2 | 1 | 0 | 0 | 0 | 1 | 0 |
| X10 | 495 | 1 | 2 | 1 | 4 | 4 | 0 | 0 | 0 | 0 | 1 |
| Y | 0 | -60 | -50 | -37 | -45 | -56 | 0 | 0 | 0 | 0 | 0 |
Составленная симплекс-таблица соответствует начальному базису и начальной опорной точке ОДР. Переход к очередной опорной точке в процессе поиска оптимального решения сопровождается составлением новой симплекс-таблицы.
Каждая симплекс-таблица анализируется по критериям допустимости и оптимальности базиса.
Похожие работы
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
... определение базисных решений соответст- вует идентификации экстремальных точек , осуществляемой при геометрическом представлении пространства решений . Таким об- разом , максимальное число итераций при использовании симплекс- метода равно максимальному числу базисных решений задачи ЛП , представленной в стандартной форме . Это означает , что количество итерационных процедур симплекс-метода не ...
... - метод для решения задач линейного программирования. Задачи курсовой заботы: 1. привести теоретический материал; 2. на примерах рассмотреть симплекс метод; 3. представить данную курсовую работу в виде презентации. Математическое программирование Математическое программирование занимается изучение экстремальных задач и поиском методов их решения. Задачи ...
... предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, еще до того, как компьютеры были использованы для решения линейных задач оптимизации. Формулировка задачи линейного программирования Нужно максимизировать при условиях при i = 1, 2, 3, . . ., m.. Иногда на xi также накладывается некоторый набор ограничений в виде равенств, но от ...


0 комментариев