Обзор научно-технической литературы
Линейное программирование
Целочисленное линейное программирование - метод ветвей и границ
Алгоритм
Решение задач оптимизации при помощи средства «Поиск решения» в Microsoft Excel
Постановка задачи планирования производства в общем случае
Решение поставленной задачи планирования производства
Проверка признака допустимости и оптимальности базиса
Схема программы
Навигация
Алгоритм
Решения задачи планирования производства симплекс методом
82416
знаков
8
таблиц
19
изображений
2.3.2.2 Алгоритм
Алгоритм симплекс-метода формулируется для задачи линейного программирования следующим образом:
Шаг 1. Формулировка задачи линейного программирования в канонической форме на основе метода искусственного базиса, так чтобы в матрице ограничений существовала единичная базисная матрица. Для этого необходимо дополнить матрицу ограничений единичными столбцами, которые должны в совокупности с исходными столбцами матрицы ограничений обеспечивать существование единичной базисной матрицы. При этом естественным образом должны быть введены соответствующие искусственные переменные, которые включаются в целевую функцию с большими положительными весовыми коэффициентами для задачи на минимум. В результате запишем исходную матрицу ограничений 
. в симплекс-таблицу(*), а коэффициенты целевой функции 
запишем в строку этой таблицы. В таблицу(*) также включим компоненты исходного базисного решения, определяемого вектором 
Таблица (*)
| #№ | Базисные столбцы | Bs | Базисное решение Xs | C1 | C2 | … | Cm | Cm+1 | … | Ck | … | Cn |
| A1 | A2 | … | Am | Am+1 | … | Ak | … | An | ||||
| 1 | A1 |
|
| 1 | 0 | … | 0 |
| … |
| … |
|
| 2 | A2 |
|
| 0 | 1 | … | 0 |
| … |
| … |
|
| … | … | … | … | … | … | … | … | … | … | … | … | … |
| l | Al |
|
| 0 | 0 | … | 0 |
| … |
| … |
|
| … | … | … | … | … | … | … | … | … | … | … | … | … |
| m | Am |
|
| 0 | 0 | … | 1 |
| … |
| … |
|
| Оценки |
|
| … |
|
| … |
| … |
|
Шаг 2. Вычисление характеристических разностей (оценок) по формулам и запись оценок в 
-ю строку симплекс-таблицы.
Шаг 3. Вычисление оценки 
, удовлетворяющей условию:
Если все 
, то в соответствии с выполнением критерия оптимальности вектор 
— оптимальное решение, и далее следует перейти к шагу 9, иначе — к шагу 4.
Шаг 4. Вычисление нового базисного решения 
из условия:
Шаг 5. Вычисление компонент нового базисного решения 
по формулам:
Шаг 6. Вычисление элементов новой симплекс-таблицы для 
-й итерации метода по формулам:
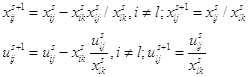
Шаг 7. Корректировка симплекс-таблицы с учетом изменений коэффициентов целевой функции, соответствующих новому базисному решению. Формируем таблицу (**).
Таблица (**)
| #№ | Базисные столбцы |
| Базисное решение Xs | C1 | C2 | … | Cm | m+1 | … | Ck | … | Cn |
| A1 | A2 | … | Am | Am+1 | … | Ak | … | An | ||||
| 1 | A1 |
|
| 1 | 0 | … | 0 |
| … |
| … |
|
| 2 | A2 |
|
| 0 | 1 | … | 0 |
| … |
| … |
|
| … | … | … | … | … | … | … | … | … | … | … | … | … |
| l | Al |
|
| 0 | 0 | … | 0 |
| … |
| … |
|
| … | … | … | … | … | … | … | … | … | … | … | … | … |
| m | Am |
|
| 0 | 0 | … | 1 |
| … |
| … |
|
| Оценки |
|
| … |
|
| … |
| … |
|
Шаг 8. Переход к шагу 2.
Шаг 9. Остановка, регистрация оптимального решения.
Таким образом, сформулированный алгоритм определяет конечную последовательность шагов, необходимых для вычисления оптимального решения.
Похожие работы
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
... определение базисных решений соответст- вует идентификации экстремальных точек , осуществляемой при геометрическом представлении пространства решений . Таким об- разом , максимальное число итераций при использовании симплекс- метода равно максимальному числу базисных решений задачи ЛП , представленной в стандартной форме . Это означает , что количество итерационных процедур симплекс-метода не ...
... - метод для решения задач линейного программирования. Задачи курсовой заботы: 1. привести теоретический материал; 2. на примерах рассмотреть симплекс метод; 3. представить данную курсовую работу в виде презентации. Математическое программирование Математическое программирование занимается изучение экстремальных задач и поиском методов их решения. Задачи ...
... предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, еще до того, как компьютеры были использованы для решения линейных задач оптимизации. Формулировка задачи линейного программирования Нужно максимизировать при условиях при i = 1, 2, 3, . . ., m.. Иногда на xi также накладывается некоторый набор ограничений в виде равенств, но от ...
0 комментариев