Постройте сечение треугольной пирамиды РАВС плоскостью, которая проходит через внутреннюю точку К основания АВС и параллельна грани РАВ (рис.25)

3.05. Постройте сечение треугольной пирамиды РАВС плоскостью, которая проходит через внутреннюю точку К основания АВС и параллельна грани РАВ (рис.25).

Решение: Плоскость сечения проходит через точку К, пересекает грани АРС, СРВ и АВС пирамиды и параллельна АРВ. Следовательно, прямые пересечения с гранями параллельны соответствующим ребрам грани АРВ. Построение следует начать с нижнего основания через известную точку К. Далее через полученные точки пересечения с ребрами АС и ВС провести параллельные прямые АР и ВР соответственно.

  5.2. Уроки применения знаний, умений и навыков

1.05. Докажите, что середины ребер АР, СР, ВС и АВ тетраэдра РАВС лежат в одной плоскости. Определите вид фигуры, вершинами которой служат эти точки (модификация задачи, приведенной в пункте 4.2.3).

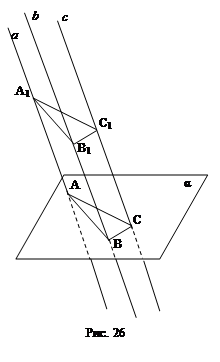1.06. Треугольник АВС лежит в плоскости α. Через его вершины проведены параллельные прямые, не лежащие в плоскости α. На них отложены равные отрезки АА₁, ВВ₁ и СС₁ по одну сторону от α. Докажите, что ∆АВС и ∆А₁В₁С₁ равны (рис. 26).

Решение: Используется: способ задания плоскости через параллельные прямые (попарное рассмотрение заданных параллельных прямых); определение параллелограмма (достаточно равенства и параллельности одной пары противолежащих сторон (по условию)); условие равенства треугольников по трем сторонам.

1.07. Прямая АВ пересекает плоскость α. Через концы отрезка АВ и его середину С проведены параллельные прямые, пересекающие плоскость α в точках А₁, В₁ и С₁. Рассмотрите случаи: 1) отрезок АВ не пересекает плоскость α (рис. 27а); 2) отрезок АВ пересекает α (рис. 27б). В каждом случае найдите: а) длину отрезка СС₁, если: АА₁ = 7, ВВ₁ = 5; б) длину отрезка АА₁, если ВВ₁ = 7, СС₁= 11.

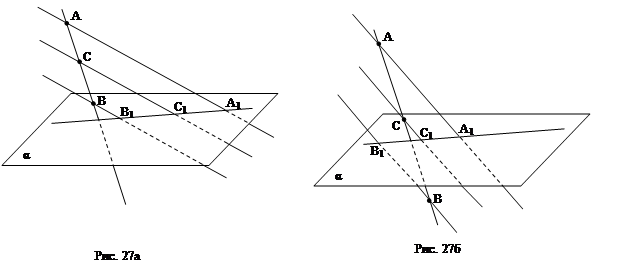
Решение: а) Точки А, В и С лежат на одной прямой (из пересечения параллельных прямых с прямой АВ и плоскостью α). В₁С₁ = С₁А₁ (по теореме Фалеса). СС₁ – средняя линия трапеции АА₁ВВ₁.

1.     

2.     

б) Сделаем выносной рисунок пересечения АВ и А₁В₁ и проведем через точку В прямую, параллельную прямой А₁В₁ (рис. 27в).

A₁L = 5 (т.к. BL ‌|| A₁B₁)

CL₁ – средняя линия в ∆АLВ

1.     

2.     

1.08. Через вершины А, В, С и D параллелограмма ABCD, расположенного в одном полупространстве относительно плоскости α, точку О пересечения его диагоналей и центроид М треугольника BCD проведены параллельные прямые, которые пересекают данную плоскость α соответственно в точках А₁, В₁, С₁, D₁, О₁, М₁. Найдите ММ₁, ОО₁ и DD₁, если АА₁ = 17, СС₁ = 5, ВВ₁ = 15 (рис. 28).

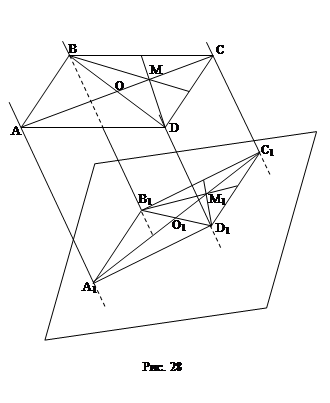Решение: В задаче используется выделение фигуры из состава чертежа, чертеж рассматривается с разных точек.

АСС₁А₁ – трапеция (параллельные прямые АА₁ и ВВ₁ задают плоскость). ОО₁ – средняя линия трапеции: .

BDD₁B₁ – трапеция: .

ОСС₁О₁ – трапеция.

ОМ = ОС (свойство пересечения медиан треугольника), О₁М₁ = О₁С₁ (аналогично). Следовательно, .

1.09. Докажите, что отрезки, соединяющие середины противолежащих ребер тетраэдра, пересекаются в одной точке и делятся этой точкой пополам (рис. 29).

Решение: ML || DB, NK || DB (как средние линии треугольников ADB и CDB соответственно), ML = NK. NMLK – параллелограмм (параллельные прямые задают плоскость). Из свойства диагоналей треугольника следует, что отрезки, соединяющие середины противолежащих ребер тетраэдра пересекаются и точкой пересечения делятся пополам. Доказательства для ОР аналогично.

2.08. В правильном тетраэдре DABC, все ребра которого равны 6, точка К лежит на ребре BD так, что DК = 2; точка М лежит на ребре ВС так, что ВМ = 4; точка Р – середина ребра АВ. а) Докажите, что КМ параллельна плоскости ADC. б) Докажите, что РМ не параллельна плоскости ADC. в) Проведите через точку Р прямую, параллельную плоскости ADC и пересекающую ребро DB в точке L. Найдите длину LK. г) Постройте сечение тетраэдра плоскостью, проходящей через точки Р и К параллельно АС (рис.30).

Решение: а) По теореме Фалеса: DC ||КМ. По признаку параллельности прямой и плоскости: (АDC) ||КМ.

б) РМ не параллельна АС (СМ≠АР), следовательно, они пересекаются, так как лежат в одной плоскости. Тогда, РМ не параллельна плоскости ADC.

в) По теореме Фалеса: DL = 3. Тогда, LK = 1.

г) (PKS) – искомое сечение, где PS – средняя линия треугольника АВС.

2.09. Основанием правильной четырехугольной пирамиды PABCD является параллелограмм ABCD. Постройте ее сечение плоскостью, проходящей через АВ и точку К, лежащую в грани: а) ВСР (рис. 31а); б) DCP (рис. 31б). Какая фигура получается в сечении?

В обоих случаях – равнобокая трапеция.

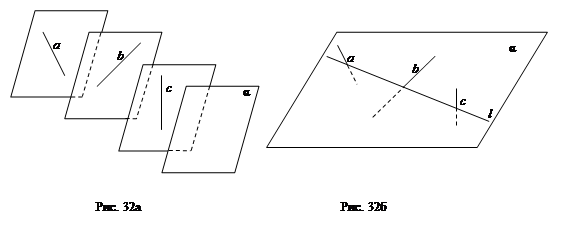
2.10. Даны три попарно скрещивающиеся прямые а, b и с. Всегда ли существует плоскость: а) параллельная каждой из этих прямых (рис. 32а); б) пересекающая каждую из них (рис. 32б)? Ответ обоснуйте и выполните соответствующий рисунок.

Решение: а) Плоскость, параллельная каждой из скрещивающихся прямых существует, если данные прямые лежат в параллельных плоскостях.

б) Плоскость, пересекающая каждую из скрещивающихся прямых, существует, если существует прямая, принадлежащая этой плоскости, которая пересекает каждую из данных прямых.

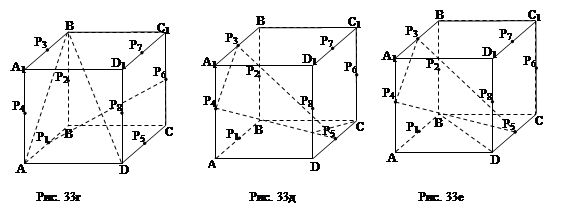
2.11. Дан куб ABCDA₁B₁C₁D₁. Пусть Р₁, Р₂, Р₃, Р₄, Р₅, Р₆, Р₇, Р₈ – середины ребер соответственно АВ, ВВ₁, В₁А_1, А₁А, CD, СС₁, С₁D₁, DD₁. Каково взаимное положение таких прямых и плоскостей, как: а) Р₃Р₄и Р₁Р₂Р₆ (рис. 33а); б) Р₇Р₈ и Р₁Р₂Р₆ (рис. 33б); в) Р₄Р₇ и Р₁Р₂Р₅ (рис. 33в); г) Р₁Р₆ и АВ₁D (рис. 33г); д) АС и Р₃Р₄Р₅ (рис. 33д); е) BD и Р₃Р₄Р₅ (рис. 33е)?

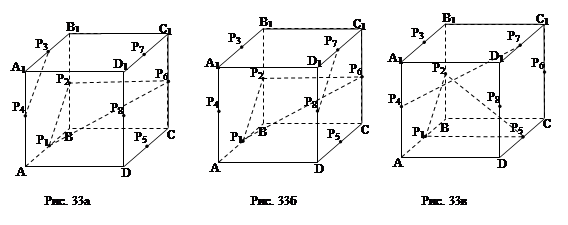
Решение: а) Р₃Р₄|| (Р₁Р₂Р₆) (признак параллельности прямой и плоскости);

б) Р₇Р₈ || (Р₁Р₂Р₆) (признак параллельности прямой и плоскости);

в) Р₄Р₇ (Р₁Р₂Р₅) (при параллельном проектировании Р₄Р₇ на вектор  прямая пересечет плоскость Р₁Р₂Р₅);

г) Р₁Р₆ || (АВ₁D) (дополним плоскость АВ₁D до плоскости АВ₁С₁D; при параллельном проектировании Р₁Р₆ на вектор  прямая будет лежать в плоскости АВ₁С₁D, следовательно, в этой плоскости существует прямая, параллельная Р₁Р₆);

д) АС || (Р₃Р₄Р₅) (дополним плоскость Р₃Р₄Р₅ до Р₃Р₄Р₆Р₅; при параллельном проектировании АС на вектор  прямая перейдет в диагональ параллелограмма Р₃Р₄Р₆Р₅, следовательно, в этой плоскости существует прямая, параллельная АС);

е) BD  Р₃Р₄Р₅ (при параллельном проектировании BD на вектор  прямая пересечет плоскость Р₃Р₄Р₅).

 Дан параллелепипед ABCDA₁B₁C₁D₁, P и Q – внутренние точки граней 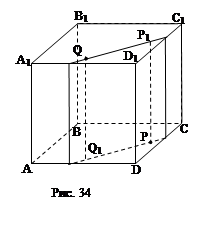соответственно ABCD и A₁B₁C₁D₁. Постройте сечение параллелепипеда плоскостью, проходящей через точки P и Q и параллельной прямой СС₁ (рис. 34).

Решение: Проведем прямые PР₁ и QQ₁, параллельные СС₁. Они задают плоскость, параллельную СС₁ и проходящую через точки P и Q.

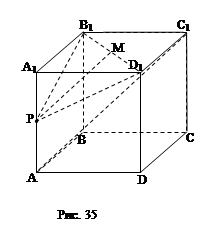2.13. Дан куб ABCDA₁B₁C₁D₁; точка Р – середина ребра АА₁. Постройте сечение куба плоскостью, проходящей через точки Р и D₁ параллельно диагонали АС грани ABCD куба (рис. 35). Найдите периметр сечения, если ребро куба равно 10.

Решение: АС₁ || (РВ₁D₁) (в этом можно убедиться, применив свойство диагоналей в параллелограмме A₁B₁C₁D₁ и теорему Фалеса к треугольнику АА₁С₁). По теореме Пифагора: . По формуле Герона: .