Навигация
220 > 110 мм,
bf1 = 220 мм.
Для назначенной ширины пояса bf1 = 22 см, дополнительные условия выполняются.После назначения bf1 находим геометрические характеристики Iy1, Wy1, Sy1.
Iy1=Iw+2· If1 = tw·hef3/12 + 2·( bf1· tf3/12 + bf1· tf ·(h/2 - tf /2)2)
Iy1= 0.8·106.83/12 + 2·( 22·1.63/12 + 22·1.6·(110/2 – 1.6 /2)2) =292700 cм4;
Wy1 = 2·Iy1/h = 292700·2/110 = 5321.82 cм3;
Sy1 = hef · tw /2·hef/4 + bf1 · tf · h0/2 = 106.2·0.8/2·106.2/4 + 22·1.6·108.4/2 = 3092 cм3;
Изгибающий момент, который может быть воспринят измененным сечением, определяется по формуле:
M1 = Wx1·Ry·γc, (3.2.21)
где γс = 1.
M1 = 5321.82·10-6·240·106·1 = 1224 кНм.
Далее находим расстояние от опоры балки до ординаты М1.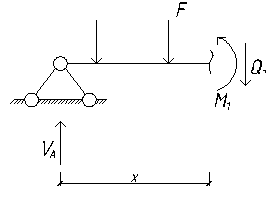
M1 - VA· x + 2·F· x – 713.052 = 0;
Решаем уравнение относительно x:
1224 – 629.163· x + 2·209.721· x – 713.052 = 0;
x = 2.436 м → x = 2.4 м.
Стык поясов в балках относим от сечения с ординатой М1 в сторону опор на 300 мм.
x – 300 = 2.4 – 0.3 = 2.1 м. Принимаем: x = 2.1 м.
Изгибающий момент в полученном сечении, будет равен:
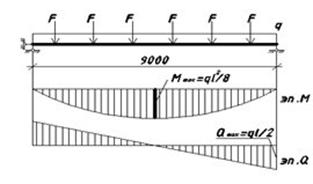
Mрасч = VA·2,1 - F· 1.25 = 629.163·2,1 – 209.721·1.25 = 1059 кНм.
В месте изменения сечения балки проводим проверки:
σ = Mрасч·γn/ Wy1 £ Ry·γc, (3.2.22)
σ = 1059·103·0.95 / 5231.82·10-6 = 189 МПа < 240 МПа;
τ = Qрасч·Sy1·γn/ Iy1·tw £ Rs·γc, (3.2.23)
Qрасч = VA - F = 629.163 –209.721 = 419.442 кН,
τ = 419.442·103·3092·10-6·0.95 / 292700·10-8·0.008 = 52.62 МПа < 139.2 МПа.
3.2.4 Проверка общей устойчивости и деформативности балок
f/l = Mmaxn·L / 9.6·EIy £ [f/L] = 1/211.667 (по СНиПу II-23-81*) (3.2.24)
Mmaxn =Mmax / k, (3.2.25)
где k = (p+q) р/(p+q) н, (3.2.26)
k = 18.95/15.92 = 1.19 > 1;
Mmaxn= 1604.366/1.19 = 1348.21 кНм;
f/l = 1348.21·103·10.2 / 9.6·2.06·105·106·363200·10-8 = 2.278·10-3 < 4.724·10-3
3.2.5 Проверка местной устойчивости балок
Стенки балок для обеспечения их местной устойчивости следует укреплять поперечными ребрами, поставленными на всю высоту стенки. Ребра жесткости нужны в том случае, если значение условной гибкости стенки:
λw = hef/tw·Ö Ry/E > 3.2, (3.2.27)
при отсутствии подвижной нагрузки
λw = 106.8/0.8·Ö 240/2.06·105= 4.557 > 3.2.
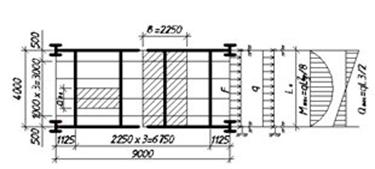
При этом расстояние между поперечными ребрами вдоль балки принимаем, а=1,7м, которое не должно превышать, а £ 2·hef. Поперечные ребра также устанавливаться в местах приложения неподвижных сосредоточенных нагрузок, от вспомогательных балок и на опорах.
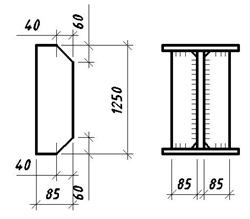
Ширина выступающей части ребра:
bh ³ hef/30 + 40мм, (3.2.28)
bh ³ 1068/30 + 40 = 75.6 мм,
после округления до размера кратного 10 мм, получим bh = 100 мм.
Толщина ребра:
ts ³ 2·bh ·Ö Ry/E, (3.2.29)
ts = 2·100·Ö 240/2.06·105 = 6.827 мм,
принимаем по сортаменту ts = 7 мм.
Расчет на устойчивость стенки проверяем по формуле:
Ö(σ/σcr)² + (τ/τcr)² £ 1, (3.2.30)
σcr = Ccr·Ry/λw², (3.2.31)
Ccr = 35.5,
σcr = 35.5·240·106 / 4.557² = 410.281 МПа;
τcr = 10.3· (1 + (0.76/μ²))·Rs/λef², (3.2.32)
μ – отношение большей стороны отсека балки к меньшей, т.е.:
μ = a/hef = 1.7/1.068 = 1.59,
λef = (d/tw) ·ÖRy/E, (3.2.33)
d – меньшая из сторон отсека балки, т.е. hef = 106.8 cм;
λef = (106.8/0.8) ·Ö240/2.06·105 = 4.557,
τcr = 10.3·(1 + (0.76/1.59²))·0.58·240·106/4.557² = 89.799 МПа;
σ = (Мср·γn /Iy)·y, (3.2.34)
τ = Q·γn /(tw·hef), (3.2.35)
y = hef/2=106.8/2=53.4 см.
На устойчивость проверим 2-ой отсек:
Мср = 891.314 кНм,
Q = 419.442 кН,
σ = (891.314·103·0.95/292700·10-8)·0.534 = 154.5 МПа;
τ = 419.442·103· 0.95/(0.008·1.068) = 46.64 МПа;
Ö(154.5/410.281)² + (46.64/89.799)² = 0.642 £ 1;
На устойчивость проверим 1-ой отсек:
Мср = 267.395 кНм,
Q = 629.163 кН,
σ = (267.395·103·0.95/292700·10-8)·0.534 = 46.34 МПа;
τ = 629.163·103· 0.95/(0.008·1.068) = 69.96 МПа;
Ö(46.34/410.281)² + (69.96/89.799)² = 0.787 £ 1;
На устойчивость проверим 3-ой отсек:
Мср = 1426.103 кНм,
Q = 209.721 кН,
σ = (1426.103·103·0.95/363200·10-8)·0.534 = 199.2 МПа;
τ = 209.721·103· 0.95/(0.008·1.068) = 23.32 МПа;
Ö(199.2/410.281)² + (23.32/89.799)² = 0.551 £ 1;
На устойчивость проверим 4-ой отсек:
Мср = 1604.366 кНм,
Q = 0 кН,
σ = (1604.366·103·0.95/363200·10-8)·0.534 = 224.1 МПа;
τ = 0·103· 0.95/(0.008·1.068) = 0 МПа;
Ö(224.1/410.281)² + (0/89.799)² = 0.546 £ 1;
Похожие работы
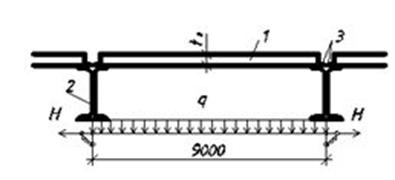
... и надежно с ним связанный, что имеет место в рассматриваемом случае. Местная устойчивость элементов прокатных профилей не проверяется, так как она обеспечена при проектировании их сортамента. 3. Расчет и конструирование главных балок. 3.1 Подбор сечения балки. Определение величины сил, которыми загружается главная балка: кН Определение величины опорных реакций и внутренних ...
... Балка настила Б2 выполняется из прокатного двутавра. Подберем 3 типа двутавров и выберем из них наиболее экономичный. 1) Двутавр с не параллельными гранями полок по ГОСТ 8239-89. 2) Двутавр балочный с параллельными гранями полок по ГОСТ 26020-83. 3) Двутавр широкополочный с параллельными гранями полок по ГОСТ 26020-83. Статический расчет Определяем расчетную схему балки. Примем разрезную ...
... монтажа. Сопряжение колонны с фундаментом принимаем также шарнирным. Рис. Расчётная схема колонны расчётные длины колонны: . Расчетная длина колонны в продольном и поперечном направлении площадки: . Расчетное значение продольной силы в колонне: Сбор нагрузок на колонну Колонна работает на сжатие под действием давления балок, опирающихся на оголовок. Выбор типа ...
... сопротивление стали Ry=240 Мпа = 24,5 кН/см2 -предел текучести стали Ru=360 Мпа = 37 кН/см2 Предельный прогиб стального листового настила: Предельный прогиб БН и ВБ: Предельный прогиб ГБ: Рассмотрим два варианта компоновки балочной площадки. 1) Нормального типа 2) Усложненного типа 2.1 Балочная клетка нормального типа Проектируем балочную клетку нормального типа. В ...
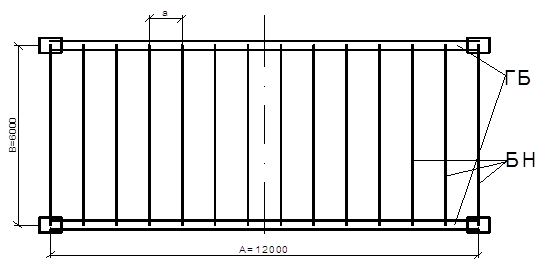
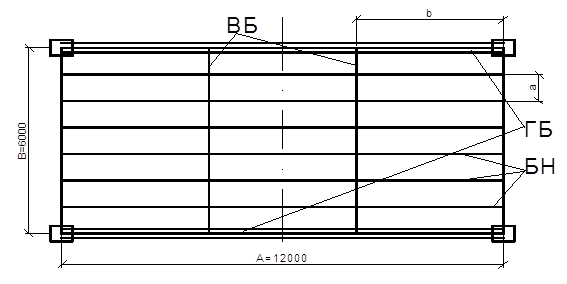

0 комментариев