Навигация
Кинематика
тема 1 кинематика точки
1.1 предмет изучения
С самого рождения и на протяжении всей своей жизни мы встречаемся с движением материи. Простейшей формой движения материи является механика. В разделе «кинематика» мы будем изучать только одну сторону механического движения – геометрическую, т.е. мы будем изучать геометрию движения тела без учета его массы и сил, действующих на него. Механически движение в общем смысле будет изучаться в разделе «динамика».
Под движением в механике мы будем понимать перемещение данного тела в пространстве и времени по отношению к другим телам.
Для определения положения движущего тела вводится система отсчета, связанная с телом, условно принимаемым за неподвижное. Движение тела происходит в пространстве и времени. Мы будем рассматривать трехмерное эвклидо пространство. За единицу длины в нем принимается 1 метр. Время считается универсальным, т. е. не зависящим от выбранной системы отсчета. За единицу времени принимается 1 секунда. В задачах механики время принимается за независимую переменную. Все остальные кинематические величины (расстояния, скорости, ускорения и т.д.) являются функциями времени.
Прежде чем изучать движение его необходимо задать, т.е. описать каким-либо математическими формулами так, чтобы можно было узнать положение тела и все его кинематические характеристики в любой момент времени.
Основная задача кинематики заключается в том, чтобы по известному закону движения тела (или какой-либо его точки) найти все остальные
кинематические характеристики движения.
Изучение кинематики мы начнем с изучения движения простейшего тела – точки, т.е. такого тела, размерами которого можно пренебречь и рассматривать его как геометрическую точку.
1.2 Способы задания движения точки
Мы будем рассматривать три способа задания движения: векторный, координатный и естественный.
1.2.1 Векторный способ
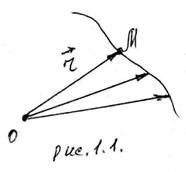
Положение движущейся точки М определяется с помощью радиуса вектора 
, проведенного из некоторого неподвижного центра О в эту точку (рис. 1.1). В процессе движения этот вектор изменяется по величине и направлению, т.е. является функцией времени. Зависимость
(1.1)
называется уравнением движения (или законом движения) в векторной форме. Линия, описываемая концом этого вектора называется траекторией движения.
|
1.2.2 Координатный способ
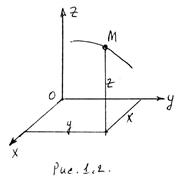
С неподвижным центром О связывается неподвижная система координат ОХ у Z. Положение точки определяется тремя координатами: х, у, z (рис. 1.2). В процессе движения эти координаты изменяются, т.е. они являются функциями времени.
|
Зависимости
х=f1(t); у=f2(t); z=f3(t) (1.2)
называются уравнениями движения точки в координатной форме. Эти уравнения являются одновременно параметрическими уравнениями траектории движения (параметром является t).
Чтобы получить уравнение траектории в явной форме, надо из уравнений (1.2) исключить параметр t.
1.2.3 Естественный способ
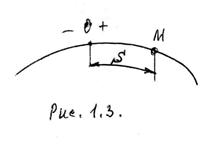
При естественном способе задания движения траектория заранее известна. На траектории выбирается начало отсчета (т. 0) и устанавливается положи-тельное и отрицательное направления отсчета.
Положение точки на траектории однозначно определяется криволинейной координатой S, измеряемой вдоль траектории. Зависимость
S = f(t) (1.3)
называется уравнением движения в естественной форме.
|
1.2.4 Связь между способами задания движения
Координатный векторный способы связаны зависимостью:
(1.4)
где 
- единичные орты координатных осей.
Переход от координатного способа к естественному:
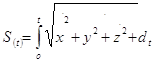
здесь: 
; 
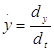
(т.е. здесь и в дальнейшем производная по времени обозначается точкой над буквой).
Похожие работы
... геометрическую сумму путем сложения векторов). Решить полученную систему уравнений. Подставить в решение общего вида значения величин и произвести вычисления. На примерах решения типовых задач на относительность движения покажем применение данного способа решения. Задача № 1. Два поезда движутся равномерно друг за другом. Скорость первого 80 км/ч, а второго 60 км/ч. Какова скорость второго поезда ...
... при двух значениях частоты вынуждающего фактора, т.е. тогда когда собственная частота колебаний корпуса двигателя совпадет с частотой вращения кривошипа. ωo = ω ωo = 2ω Значит, критическими оборотами для двигателя будут две частоты, одна – равная частоте собственных колебаний корпуса, другая равная половине частоты собственных колебаний. Для наиболее ясной картины построим ...
... трех попыток, а затем - средний коэффициент КЗ 3 с Таблица 2. Количество испытуемых, участвовавших в эксперименте Испытуемые Классы 2-й 3-й 4-й 5-й 6-й 7-й Возраст, лет 7-8 8-9 9-10 10-11 11-12 12-13 Кинематика скоростного бега Мальчики 21/26 25/22 21/22 23/22 23/22 21/25 Девочки 26/24 22/24 21/22 20/22 20/22 22/16 Двигательная ...
... 630 м со скоростью 48,6 км/ч и электричка длиной 120 м со скоростью 102,6 км/ч. В течение какого времени электричка будет обгонять товарный поезд? Ф.1.14. По одному направлению из одной точки начали одновременно двигаться два тела: одно равномерно со скоростью 9,8 м/с, другое - равноускоренно без начальной скорости с ускорением 9,8 см/с2. Через какое время второе тело догонит первое? Ф.1.15. ...
0 комментариев