Навигация
Метод найменших квадратів для лінійної моделі
3.2 Метод найменших квадратів для лінійної моделі
Розглянемо найбільш важливий для практики окремий випадок МНК, коли модель є лінійною.
Для простоти опису перетворень пронормуємо змінні хij,уi. Наступним чином:
![]()
де

Тоді
![]()
Надалі будемо вважати, що розглянуті змінні пронормовані описаним образом, і верхні індекси опустимо. Для полегшення демонстрації основних ідей приймемо досить природні припущення.
1. Для розглянутих змінних існують наступні межі:
![]()
2. Кількість досвідів n таке, що можна користуватися асимптотичними результатами, отриманими при ![]()
3. Погрішності виміру задовольняють одному з наступних типів обмежень:
Тип 1. Абсолютні погрішності виміру обмежені згідно (4.1.3):
Тип 2. Відносні погрішності виміру обмежені:
![]()
Тип 3. Обмеження накладені на суму погрішностей:
![]()
Перейдемо до обчислення нотни оцінки МНК. Справедлива рівність:

Скористаємося наступною теоремою з теорії матриць.
Теорема. Якщо функція f(λ) розкладається в степеневий ряд у колі збіжності |λ – λ0| < r, тобто
![]()
то це розкладання зберігає силу, якщо скалярний аргумент замінити будь-якою матрицею А, характеристичні числа якої λk, k = 1,…,n, лежать всередині кола збіжності.
![]()
Легко переконатися, що:

Це випливає з послідовності рівностей:

Застосуємо наведену вище теорему з теорії матриць, припускаючи
А = Δ Z і приймаючи, що власні числа цієї матриці задовольняють нерівності |λk|<1. Тоді одержимо:

Підставивши останнє співвідношення на закінчення згаданої теореми, одержимо:

Для подальшого аналізу знадобиться допоміжне твердження. Виходячи із припущень 1-3, доведемо, що:

Доведення. Справедлива рівність

де ![]() - спроможні і незміщені оцінки дисперсій і коефіцієнтів коваріації, тобто
- спроможні і незміщені оцінки дисперсій і коефіцієнтів коваріації, тобто
![]()
тоді
![]()
де ![]()
Інакше кажучи, кожен елемент матриці, позначеної як о(1/n), є нескінченно малою величиною порядку 1/n. Для розглянутого випадку cov(x) = E, тому
![]()
Припустимо, що n досить велике і можна вважати, що власні числа матриці о(1/n) менше одиниці по модулю, тоді

що і було потрібно довести.
Підставимо доведене асимптотичне співвідношення у формулу для приросту![]() *,одержимо
*,одержимо
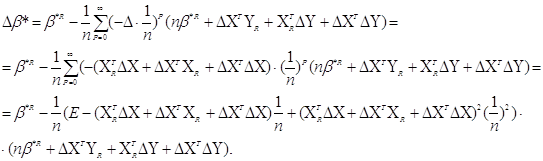
Виразимо Δ![]() * відносно приросту ΔХ, ΔY до 2-гo порядку
* відносно приросту ΔХ, ΔY до 2-гo порядку
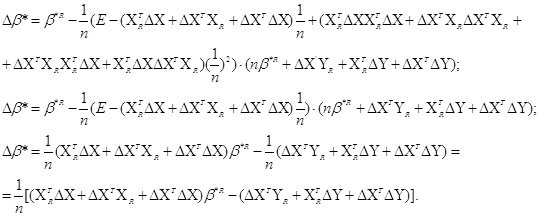
Перейдемо від матричної до скалярної форми, опускаючи індекс (R):
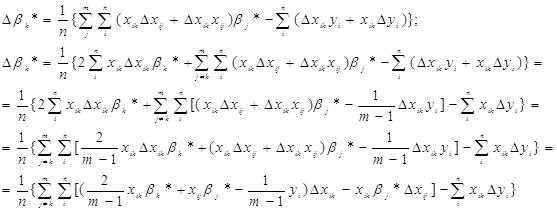
Будемо шукати max(|Δ![]() k*|) по Δxij і Δyi (i=1,…, п;j=1,…, m). Для цього розглянемо всі три раніше введених типи обмежень на похибки виміру.
k*|) по Δxij і Δyi (i=1,…, п;j=1,…, m). Для цього розглянемо всі три раніше введених типи обмежень на похибки виміру.
Тип 1 (абсолютні похибки виміру обмежені). Тоді:
![]()
Тип 2 (відносні похибки виміру обмежені). Аналогічно одержимо:
![]()
Тип З (обмеження накладені на суму похибок). Припустимо, що |Δ![]() k*| досягає максимального значення при таких значеннях погрішностей Δxij і Δyi,
k*| досягає максимального значення при таких значеннях погрішностей Δxij і Δyi,
які ми позначимо як:
![]()
тоді:

Через лінійність останнього вираження і виконання обмеження типу 3:

Для спрощення запису зробимо наступні заміни:

Тепер для досягнення поставленої мети можна сформулювати наступне завдання, що розділяється на m типових завдань оптимізації:

при обмеженнях

Перепишемо функції, що мінімізуємо, в наступному вигляді:

Очевидно, що fik > 0.
Легко бачити, що

Отже, необхідно вирішити nm завдань

при обмеженнях "типу рівності":

Сформульоване завдання пошуку екстремуму функції. Воно легко вирішується. Оскільки

то максимальне відхилення МНК - оцінки k-ого параметра дорівнює
![]()
Похожие работы
... іжності між емпіричними і теоретичними частотами розподілу не можуть бути випадковими і припущення про близькість емпіричного розподілу до нормального повинна бути спростоване. Розділ 3. Кореляційний аналіз виробництва льоноволокна Одним з найважливіших завдань статистики є вивчення об'єктивно існуючих зв'язків між явищами. При дослідженні таких зв'язків з'ясовуються причинно-наслідкові ві ...
... ідного індексу, а абсолютні величини змін валового збору за рахунок даного фактора — як різницю чисельника і знаменника відповідного індексу. 2. СТАТИСТИЧНИЙ АНАЛІЗ УРОЖАЙНОСТІ ТЕХНІЧНИХ КУЛЬТУР 2.1 Аналіз рівня та факторів урожайності методом аналітичного групування Групування — невід'ємний елемент зведення, його найважливіший етап. Це процес утворення груп одиниць сукупності, однорідних ...
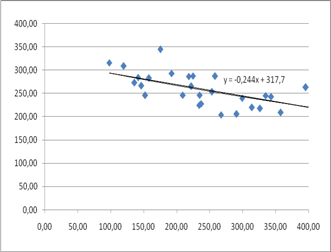
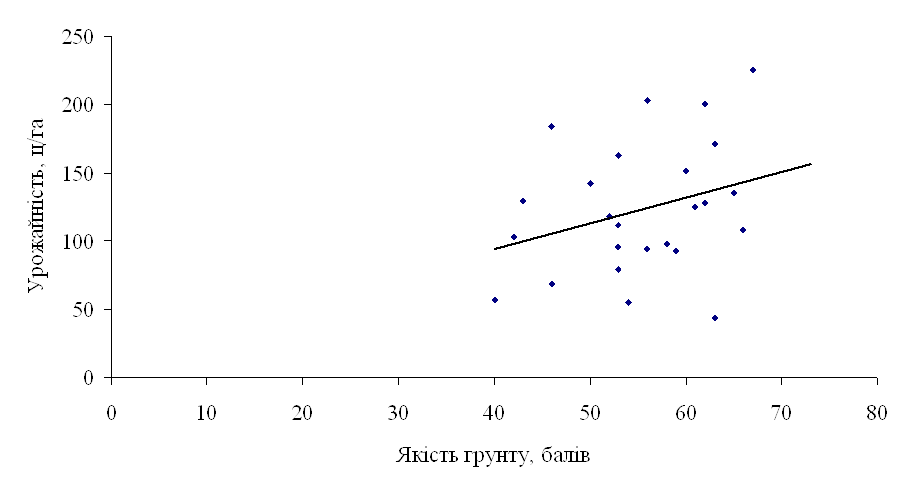
... лінію регресії (рис.4). Рис 4. Кореляційне поле залежності урожайності цукрових буряків від якості ґрунту Розділ IV. Динаміка та прогнозування урожайності цукрових буряків 4.1 Перспективи розвитку урожайності цукрових буряків в господарствах Андрушівського району Рядом динаміки називається тимчасова послідовність значень статистичних показників. Ряд динаміки складається із ...
... курсової роботи виступають річні звіти за 2004, 2005, 2006 роки, матеріали статистичної звітності та економічний паспорт ВАТ "Сонячне" Тарутинського району Одеської області 1.1. Значення, завдання та джерела даних для економіко-статистичного аналізу собівартості продукції тваринництва. Одним із найважливіших показників роботи підприємства та галузі економіки в цілому є собівартість ...



0 комментариев