Навигация
3.3 Парна регресія
Найбільш простий і одночасно найбільше широко застосовуваний окремий випадок парної регресії розглянемо докладніше. Модель має вигляд
(3.3.1)
Тут xi - значення фактора (незалежної змінної), 
- значення відгуку (залежної змінної), 
- статистичні похибки, 
- невідомі параметри, оцінювані методом найменших квадратів. Модель (3.3.1) може бути записана у вигляді:
(3.3.2)
якщо покласти
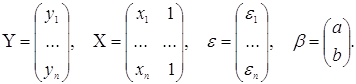
Природно прийняти, що похибки факторів описуються матрицею
У розглянутій моделі інтервального методу найменших квадратів
де X, 
- спостережувані значення фактора і відгуку, XR, yR - істині значення змінних, 
- погрішності вимірів змінних. Нехай 
- оцінка методу найменших квадратів, обчислена за спостережуваним значенням змінних, 
- аналогічна оцінка, знайдена за істинним значенням. Відповідно до раніше проведених міркувань
(3.3.3)
з точністю до нескінченно малих більш високого порядку по 
і 
. У формулі (3.3.3) використане позначення 
. Обчислимо праву частину в (3.3.3), виділимо головний лінійний член і знайдемо нотну.
Легко бачити, що
(3.3.4)
де підсумовування проводиться від 1 до n. Для спрощення позначень надалі і до кінця дійсного пункту не будемо вказувати ці межі підсумовування. З (3.3.4) випливає, що
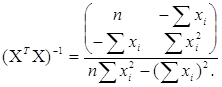(3.3.5)
Легко підрахувати, що
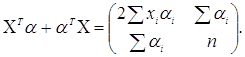(3.3.6)
Покладемо
Тоді знаменник в (3.3.5) дорівнює 
. З (3.3.5) і (3.3.6) випливає, що
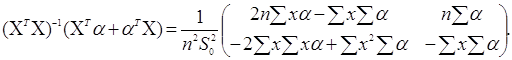(3.3.7)
Тут і далі опустимо індекс і, по якому проводиться підсумовування. З (3.3.5) і (3.3.7) випливає:
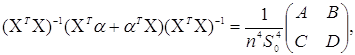(3.3.8)
де
Обчислимо основний множник в (3.3.3)
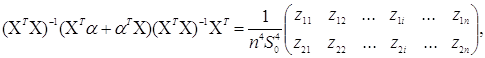(3.3.9)
де
Перейдемо до обчислення другого члена з 
в (3.3.3). Маємо
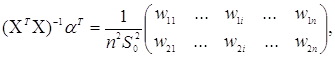(3.3.10)
де
Складаючи праві частини (3.3.9) і (3.3.10) і помножуючи на у, одержимо остаточний вид члена з 
в (3.3.3):
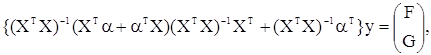(3.3.11)
де
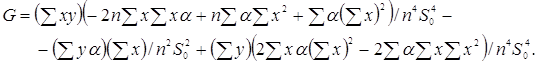
Для обчислення нотни виділимо головний лінійний член. Спочатку знайдемо частинні похідні. Маємо
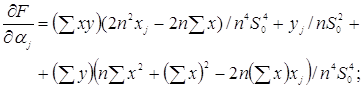(3.3.12)
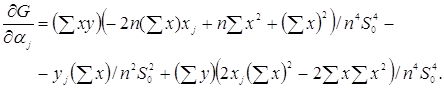
Якщо обмеження мають вигляд
то максимально можливе відхилення оцінки а* параметра а через погрішності 
таке:
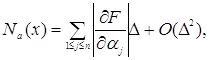(3.3.13)
де похідні задані формулою (3.3.12).
Розділ IV. Програмний продукт «Інтервальне значення параметрів»
Похожие работы
... іжності між емпіричними і теоретичними частотами розподілу не можуть бути випадковими і припущення про близькість емпіричного розподілу до нормального повинна бути спростоване. Розділ 3. Кореляційний аналіз виробництва льоноволокна Одним з найважливіших завдань статистики є вивчення об'єктивно існуючих зв'язків між явищами. При дослідженні таких зв'язків з'ясовуються причинно-наслідкові ві ...
... ідного індексу, а абсолютні величини змін валового збору за рахунок даного фактора — як різницю чисельника і знаменника відповідного індексу. 2. СТАТИСТИЧНИЙ АНАЛІЗ УРОЖАЙНОСТІ ТЕХНІЧНИХ КУЛЬТУР 2.1 Аналіз рівня та факторів урожайності методом аналітичного групування Групування — невід'ємний елемент зведення, його найважливіший етап. Це процес утворення груп одиниць сукупності, однорідних ...
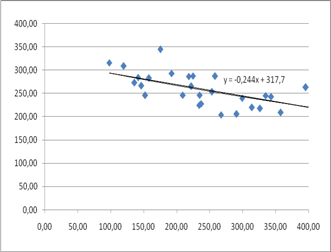
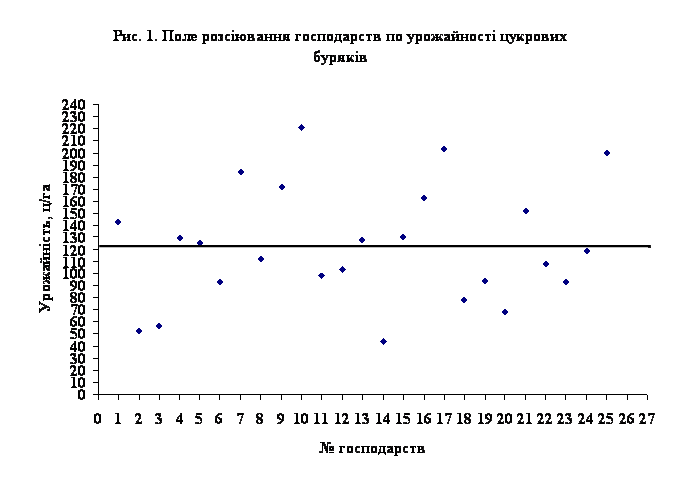
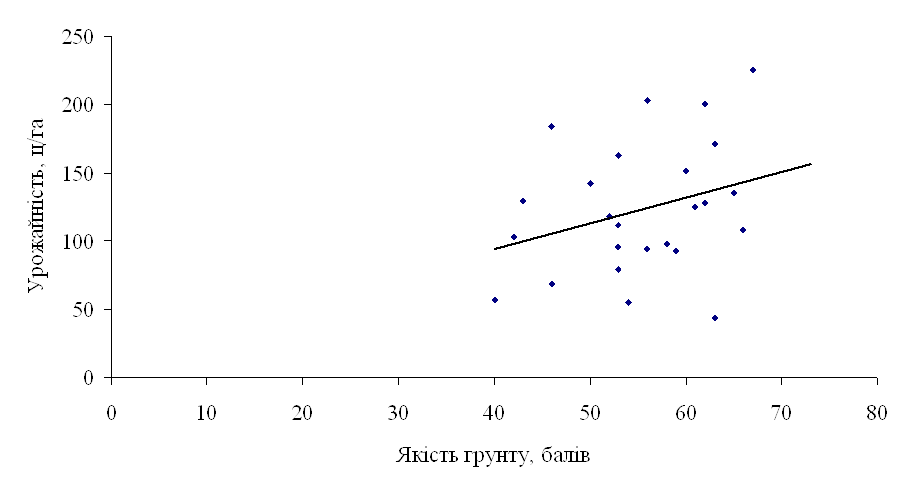
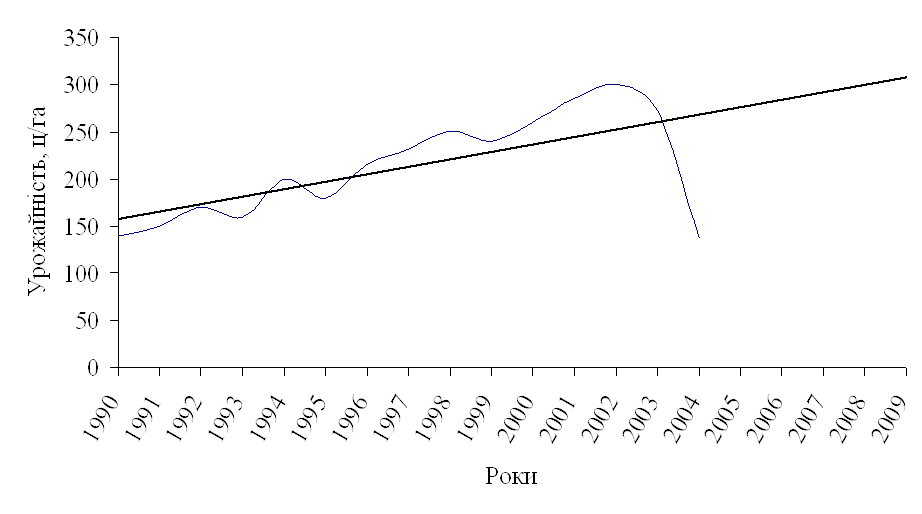
... лінію регресії (рис.4). Рис 4. Кореляційне поле залежності урожайності цукрових буряків від якості ґрунту Розділ IV. Динаміка та прогнозування урожайності цукрових буряків 4.1 Перспективи розвитку урожайності цукрових буряків в господарствах Андрушівського району Рядом динаміки називається тимчасова послідовність значень статистичних показників. Ряд динаміки складається із ...
... курсової роботи виступають річні звіти за 2004, 2005, 2006 роки, матеріали статистичної звітності та економічний паспорт ВАТ "Сонячне" Тарутинського району Одеської області 1.1. Значення, завдання та джерела даних для економіко-статистичного аналізу собівартості продукції тваринництва. Одним із найважливіших показників роботи підприємства та галузі економіки в цілому є собівартість ...
0 комментариев