Контрольная работа
1. Вычислить предел функции.
2. Вычислить производную функции.
3. Исследовать функции f(х) и g(х) и построить графики.
4. Вычислить неопределенные интегралы.
5. Вычислить площадь фигуры, ограниченной графиками функций f(х) и g(х).
6. Найти общее решение дифференциального уравнения и построить графики двух различных частных решений этого уравнения.
7. Найти частное решение дифференциального уравнения, удовлетворяющее указанному условию.
8. Найти частное решение дифференциального уравнения, удовлетворяющее указанным условиям.
9. Исследовать ряд на сходимость.
10. Найти радиус и интервал сходимости степенного ряда.
Вариант 0
1. а) 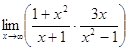 ; б)
; б) 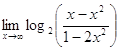 ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б)  ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = x-1, g(x) = x2 -4x + 3.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 1
1. а)  ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) 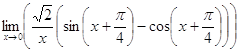 ; е)
; е) ![]() .
.
2. а) y = ln(tg x); б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = (x+2)/2, g(x) =(- x2 +7x + 2)/2.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 2
1. а)  ; б)
; б) ![]() ;
;
в) 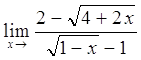 ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) 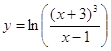 ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = x-3, g(x) = x2 +4x -3.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 3
1. а)  ; б)
; б) 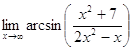 ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) =1- x, g(x) = 3 - 2x - x2.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 4
1. а) 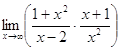 ; б)
; б) 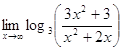 ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = x, g(x) = 2 + 2x - x2.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 5
1. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) 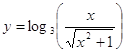 ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = x2 - x + 1, g(x) = x + 1.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 6
1. а) 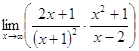 ; б)
; б)  ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б)![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = 2 - 2x2, g(x) = x+1.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 7
1. а)  ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = x2 + 3x + 1, g(x) = -2x - 3.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 8
1. а) 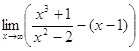 ; б)
; б) 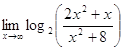 ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = -3x2 +21x - 11, g(x) = 3x + 4.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Вариант 9
1. а) 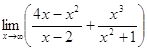 ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
2. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
3. а) ![]() ; б)
; б) ![]() ;
;
4. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
5. f(x) = 2x - 3, g(x) = -x2 + 3x - 1.
6. ![]() .
.
7. ![]()
![]() .
.
8. ![]() ;
; ![]()
![]()
9. ![]() .
.
10. ![]() .
.
Похожие работы
... численных методов (при решении реальных, а не учебных задач!) предполагает использование компьютеров с достаточным быстродействием. Использование для численного решения дифференциальных уравнений компьютерного пакета MathCAD предполагает знание алгоритма работы численных методов для разумного их применения (знание границ применимости, оценки точности, затрат компьютерных ресурсов и др.). Дело в ...
... с единицами измерений физических величин в системе MathCAD? 11. Подробно охарактеризуйте текстовые, графические и математические блоки. Лекция №2. Задачи линейной алгебры и решение дифференциальных уравнений в среде MathCAD В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами. Панель операторов с матрицами находится на панели Math. ...
... = cos(aּπּt) и нулевых начальных условиях; 3. Выводы по работе №3 В процессе данной практической работы я изучил возможности математического пакета MathCad в среде Windows для решения дифференциальных уравнений N-го порядка, используемых в инженерных расчетах электротехнических систем. Были выполнены численные методы решения дифференциальных уравнений N-го порядка. Заданное ...
... значениями и корнями дифференциального уравнения Y(I), квадрат разности, а также производит их суммирование. Далее находится величина погрешности аппроксимации и все данные выводятся на экран. Общая программа решения дифференциального уравнения с последующей аппроксимацией результатов представлена на рис. 7 вместе с программой решения дифференциального уравнения, так как из нее получают значения ...




0 комментариев