Навигация
Заменяем каждый элемент транспонированной матрицы его алгебраическим дополнением;
3. заменяем каждый элемент транспонированной матрицы его алгебраическим дополнением;
4. делим каждый полученный элемент на ![]() .
.
Понятие обратной матрицы дает возможность решать матричные уравнения. Пусть имеется уравнение вида ![]() , где
, где ![]() ,
, ![]() ,
, ![]() ,
, ![]() - некоторые матрицы, причем
- некоторые матрицы, причем ![]() - неизвестная. Для нахождения
- неизвестная. Для нахождения ![]() , прежде всего, необходимо
, прежде всего, необходимо ![]() перенести вправо:
перенести вправо: ![]() . Затем, пользуясь тем, что
. Затем, пользуясь тем, что ![]() , умножим равенство на
, умножим равенство на ![]() :
:
![]() .
.
При решении подобных уравнений необходимо учитывать, с какой стороны стоит множитель при ![]() . Если уравнение имеет вид
. Если уравнение имеет вид ![]() , то
, то
![]() .
.
Если же уравнение имеет множители при ![]() с обеих сторон
с обеих сторон
(![]() ), то
), то ![]() .
.
4. Базисный минор и ранг матрицы
Введя понятие линейной комбинации строк и столбцов матрицы, как это было сделано у векторов, можно ввести понятие их линейной зависимости и независимости.
Определение 1. Строки ![]() ,
, ![]() ,...,
,..., ![]() называются линейно зависимыми, если существуют числа
называются линейно зависимыми, если существуют числа ![]() , не все равные нулю, такие что справедливо равенство
, не все равные нулю, такие что справедливо равенство ![]() .
.
Здесь 0 - нулевая строка.
Определение 2. Строки ![]() называются линейно независимыми, если их линейная комбинация обращается в ноль лишь при условии, что
называются линейно независимыми, если их линейная комбинация обращается в ноль лишь при условии, что ![]() .
.
В этом случае линейная комбинация называется тривиальной.
Так же как и у векторов имеется соответствующая теорема.
Теорема 1. Для того чтобы строки ![]() были линейно зависимы, необходимо и достаточно, чтобы одна из них была линейной комбинацией остальных.
были линейно зависимы, необходимо и достаточно, чтобы одна из них была линейной комбинацией остальных.
Доказательство проводится так же, как и в 4 (там это разбито на две теоремы).
Теорема 2. Если в систему строк матрицы входит нулевая строка, то эти строки линейно зависимы.
Доказательство. Действительно, нулевая строка представляет собой тривиальную линейную комбинацию любых строк. Но тогда мы сразу переходим к теореме 1.
Рассмотрим теперь понятие базисного минора. Пусть имеется произвольная матрица порядка ![]() :
:
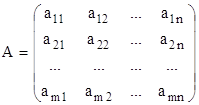 .
.
Определение 3. Минором ![]() -го порядка матрицы
-го порядка матрицы ![]() называется определитель
называется определитель ![]() -го порядка с элементами, лежащими на пересечении любых
-го порядка с элементами, лежащими на пересечении любых ![]() строк и
строк и ![]() столбцов матрицы
столбцов матрицы ![]() .
.
Определение 4. В матрице ![]() , порядка
, порядка ![]() , минор порядка
, минор порядка ![]() называется базисным, если он не равен нулю, а все остальные миноры порядка
называется базисным, если он не равен нулю, а все остальные миноры порядка ![]() равны нулю или миноров порядка
равны нулю или миноров порядка ![]() вообще нет, то есть
вообще нет, то есть ![]() совпадает с меньшим из чисел
совпадает с меньшим из чисел ![]() или
или ![]() .
.
Очевидно, что в матрице может быть несколько базисных миноров, но все они должны быть одного порядка.
Определение 5. Рангом матрицы называется порядок базисного минора. Обозначается ранг матрицы - ![]() . Строки и столбцы, на пересечении которых стоит базисный минор, называются базисными.
. Строки и столбцы, на пересечении которых стоит базисный минор, называются базисными.
Теорема 3. (Теорема о базисном миноре). Базисные строки и столбцы линейно независимы. Любая другая строка или столбец матрицы ![]() являются линейной комбинацией базисных строк или столбцов.
являются линейной комбинацией базисных строк или столбцов.
Доказательство проведем для строк. Покажем вначале, что базисные строки линейно независимы. Если бы они были линейно зависимы, то одна из этих строк была бы линейной комбинацией остальных. Тогда на основании свойств определителя эту комбинацию можно вычесть из указанной строки и получить на ее месте ноли. Но если вся строка состоит из нолей, то минор равен нулю, что противоречит теореме.
Докажем вторую часть этой теоремы. Рассмотрим любой минор ![]() -го порядка, включающий в себя базисный. Расположим базисный минор в левом верхнем углу:
-го порядка, включающий в себя базисный. Расположим базисный минор в левом верхнем углу:
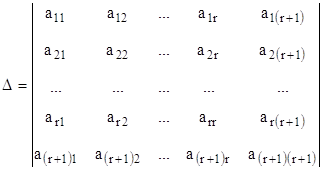 .
.
По определению данный минор равен нулю. Раскроем его по последнему столбцу:
![]() .
.
Здесь ![]() , разделим на него все равенство:
, разделим на него все равенство:
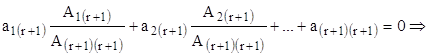
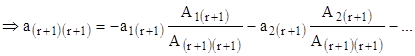
Из полученного выражения следует, что ![]() -ая строка является линейной комбинацией базисных строк.
-ая строка является линейной комбинацией базисных строк.
Отсюда можно сделать вывод, что число линейно независимых строк или столбцов равно рангу матрицы. Это свойство используется для практического вычисления ![]() .
.
Литература
1. Александров В.В., Потапов М.К., Пасиченко П.И., Потапов М.К. Александров В.В., Потапов М. К и др. Алгебра, тригонометрия и элементарные функции. Учебник. М: Высшая школа, 2001. - 736с.
2. Тоом А., Гельфанд И., Львовский С. Тригонометрия. МЦМНО, 2003. - 200с.
3. Баврин И.И. Высшая математика - 1980 г.
4. Дж. Голуб, Ч. Ван Лоун Матричные вычисления. - М.: Мир, 1999.
5. Беллман Р. Введение в теорию матриц. - М.: Мир, 1969.
6. Гантмахер Ф.Р. Теория матриц (2-е издание). - М.: Наука, 1966.
7. Ланкастер П. Теория матриц. - М.: Наука, 1973.
Похожие работы
... , с помощью которых в последующем решение систем линейных уравнений станет намного проще, понятнее и быстрее. Цель моей работы заключается в том, чтобы изучить различные способы решения систем линейных уравнений для применения их на практике. Для достижения любой цели необходимо выполнить какие-то определенные задачи. Мне нужно выполнить следующие задачи: исследовать литературу по темам матриц, ...
... с единицами измерений физических величин в системе MathCAD? 11. Подробно охарактеризуйте текстовые, графические и математические блоки. Лекция №2. Задачи линейной алгебры и решение дифференциальных уравнений в среде MathCAD В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами. Панель операторов с матрицами находится на панели Math. ...
... , соответствующим матрице порядка , называется число, равное . Обозначается определитель одним из символов (3.1 3) Приведенное выражение представляет собой правило вычисления определителя -го порядка по элементам первой строки соответствующей ему матрицы и по минорам элементов этой строки, которые являются определителями порядка . Для это правило дает: . В приведенном ...
... f ¢(xо) = 0, >0 (<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные. На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b]. Пример 3.22. Найти экстремумы функции f(x) ...
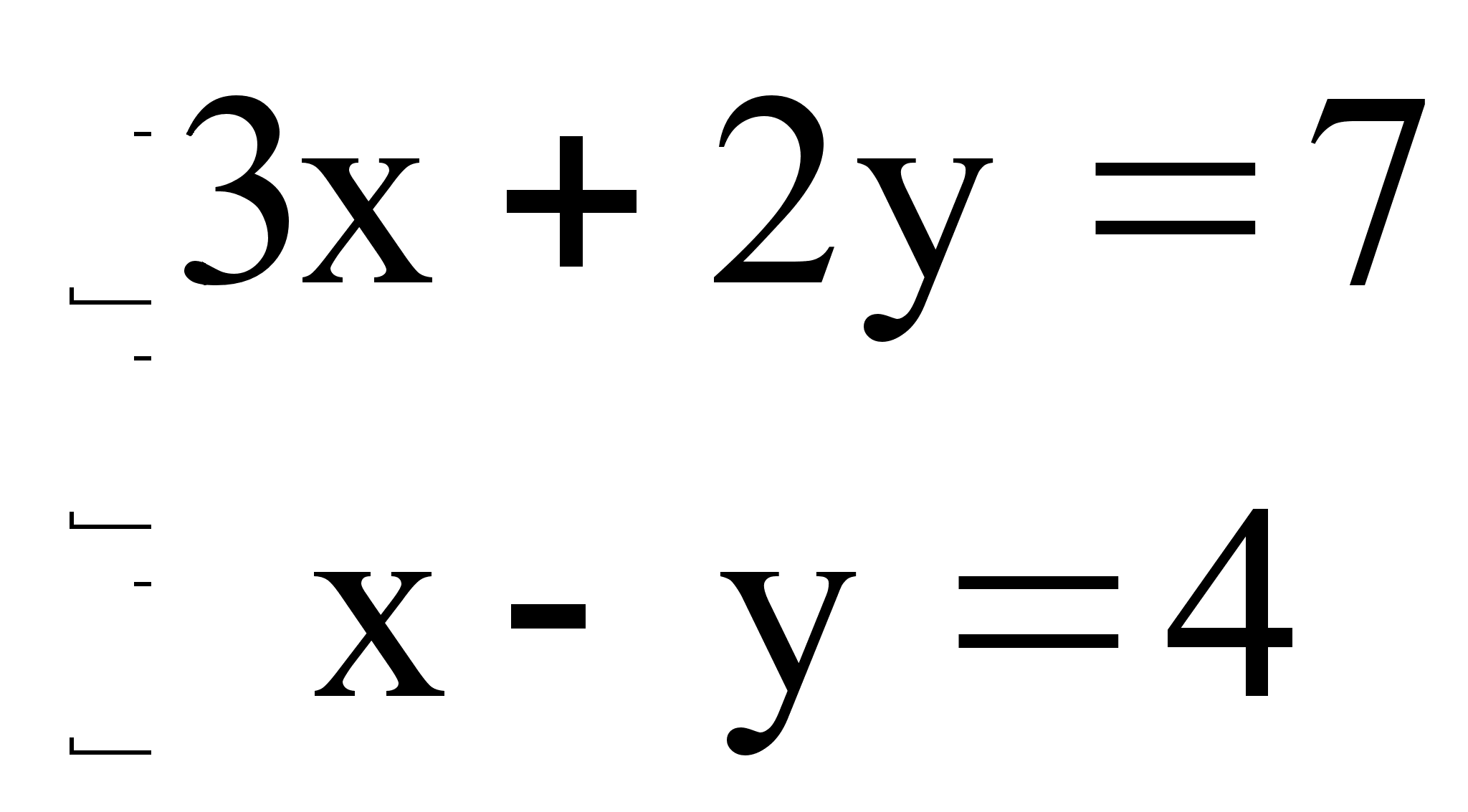

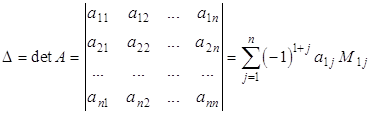


0 комментариев