Навигация
Системи випадкових величин
СИСТЕМИ ВИПАДКОВИХ ВЕЛИЧИН
(реферат)
Вступ
N-вимірний вектор ![]() (t-індекс транспонування) називається випадковим, якщо його координати є випадковими величинами. Вектор
(t-індекс транспонування) називається випадковим, якщо його координати є випадковими величинами. Вектор ![]() називають дискретним, якщо його координати - дискретні випадкові величини, неперервним, якщо його компоненти - неперервні випадкові величини і змішаним, якщо частина його компонент – дискретні випадкові величини, а інша частина – неперервні випадкові величини. Випадкові N-вимірні вектори називають ще системою N випадкових величин або багатовимірними випадковими величинами. В подальшому розглядаються двовимірні випадкові вектори (системи двох випадкових величин), які позначаються
називають дискретним, якщо його координати - дискретні випадкові величини, неперервним, якщо його компоненти - неперервні випадкові величини і змішаним, якщо частина його компонент – дискретні випадкові величини, а інша частина – неперервні випадкові величини. Випадкові N-вимірні вектори називають ще системою N випадкових величин або багатовимірними випадковими величинами. В подальшому розглядаються двовимірні випадкові вектори (системи двох випадкових величин), які позначаються ![]() .
.
1. Розподіли системи двох випадкових величин
Система двох дискретних випадкових величин однозначно визначається сумісним розподілом ймовірностей, який можна задати матрицею
y1 y2 … ym
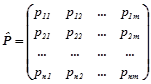
![]() , (1.1)
, (1.1)
(![]() ).
).
Стовпчики матриці відповідають значенням ![]() випадкової величини Y , а рядки – значенням
випадкової величини Y , а рядки – значенням ![]() випадкової величини X. Події
випадкової величини X. Події ![]() утворюють повну групу подій, тому сума елементів матриці
утворюють повну групу подій, тому сума елементів матриці ![]() дорівнює 1:
дорівнює 1:
![]() .
.
Розподіли
![]() ,
,
![]()
називають розподілами компонент системи двох випадкових величин ![]() . Події
. Події ![]() ,
, ![]() ,...,
,..., ![]() є несумісними, тому за теоремою додавання ймовірностей несумісних подій сума елементів і-рядка матриці
є несумісними, тому за теоремою додавання ймовірностей несумісних подій сума елементів і-рядка матриці ![]() дорівнює ймовірності значення
дорівнює ймовірності значення ![]() :
:
![]() .(1.1а)
.(1.1а)
Аналогічно, сума елементів j-стовпчика дорівнює ймовірності значення ![]() :
:
![]() .(1.1b)
.(1.1b)
Приклад 1.1. Система двох випадкових величин ![]() задана сумісним розподілом
задана сумісним розподілом
y1 y2
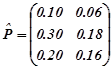
![]()
Знайти розподіли компонент системи випадкових величин.
Розв’язування. За формулами (1.1а) та (1.1b)
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
; ![]() .
.
Отже, розподіли компонент
![]()
![]() .
.
Будь-який двовимірний випадковий вектор (неперервний чи дискретний) однозначно визначається інтегральною функцією сумісного розподілу
![]() , (1.2)
, (1.2)
яка визначає ймовірність того, що випадкова величина X приймає значення менше ніж x, а ![]() - менше ніж y. Геометрична інтерпретація інтегральної функції сумісного розподілу полягає в тому, що вона визначає ймовірність попадання випадкової точки
- менше ніж y. Геометрична інтерпретація інтегральної функції сумісного розподілу полягає в тому, що вона визначає ймовірність попадання випадкової точки ![]() у нескінченний заштрихований квадрат із вершиною в точці
у нескінченний заштрихований квадрат із вершиною в точці ![]() (рис 1.1).
(рис 1.1).
Інтегральна функція розподілу випадкового вектора ![]() має такі очевидні властивості.
має такі очевидні властивості.
Властивість 1.
![]() .
.
Властивість 2. Функція ![]() неспадна по кожному аргументу
неспадна по кожному аргументу
![]() , якщо
, якщо ![]() ;
;
![]() , якщо
, якщо ![]() .
.
Властивість 3. Мають місце граничні співвідношення
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Властивість Для функція ![]() мають місце ще і такі граничні співвідношення
мають місце ще і такі граничні співвідношення
![]() ,
,
![]() ,
,
![]() - інтегральна функція розподілу компоненти X випадкового вектора
- інтегральна функція розподілу компоненти X випадкового вектора ![]() .
.
![]() - інтегральна функції розподілу компоненти Y випадкового вектора
- інтегральна функції розподілу компоненти Y випадкового вектора ![]() .
.
З використанням функції розподілу (1.2) легко можна обчислити ймовірність попадання випадкової точки у напівсмугу ![]() та
та ![]() (рис 1.2)
(рис 1.2)
![]() , (1.3а)
, (1.3а)
![]() .(1.3б)
.(1.3б)
Імовірність попадання випадкової точки у напівсмугу дорівнює приросту інтегральної функції сумісного розподілу по відповідному аргументу.
Доведення. Імовірність попадання у напівсмугу ![]() дорівнює різниці ймовірності попадання точки у нескінченний квадрат з вершиною
дорівнює різниці ймовірності попадання точки у нескінченний квадрат з вершиною ![]() (
(![]() )і ймовірності попадання точки у нескінченний квадрат з вершиною
)і ймовірності попадання точки у нескінченний квадрат з вершиною ![]() (
(![]() . Звідси і слідує рівність (1.3а)
. Звідси і слідує рівність (1.3а)
Імовірність попадання випадкової точки у прямокутник утворений прямими
![]()
(рис.1.3) обчислюється за формулою
![]() (1.4)
(1.4)
Доведення. Імовірність попадання у прямокутник дорівнює різниці ймовірності попадання точки у напівсмугу ![]() (
(![]() )і ймовірності попадання у напівсмугу
)і ймовірності попадання у напівсмугу ![]() (
(![]() ). Звідси і слідує рівність (1.3а)
). Звідси і слідує рівність (1.3а)
Приклад 1.2. Знайти ймовірність пападання випадкової точки ![]() у прямокутник обмеженний прямими
у прямокутник обмеженний прямими ![]() ,
, ![]() ,
, ![]() ,
, ![]() , якщо відома інтегральна функція сумісного розподілу
, якщо відома інтегральна функція сумісного розподілу
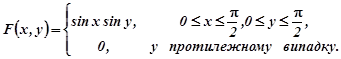
Розв’язування. За формулою (1.4) в якій ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
![]()
![]()
Система двох неперервних випадкових величин ![]() однозначно визначається густиною сумісного розподілу ймовірностей
однозначно визначається густиною сумісного розподілу ймовірностей
![]() . (1.5)
. (1.5)
Приклад 1.3. Знайти густину сумісного розподілу системи випадкових величин![]() , якщо відома інтегральна функція сумісного розподілу
, якщо відома інтегральна функція сумісного розподілу
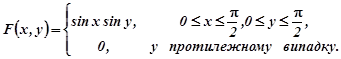
Розв’язування. За формулою (1.5)
![]()
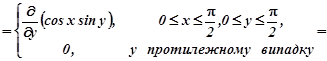
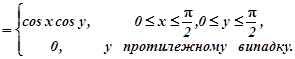
Інтегральна функція сумісного розподілу неспадна по кожному аргументу і тому
![]() .
.
За відомою густиною сумісного розподілу інтегральну функцію сумісного розподілу можна визначити за формулою
![]() (1.6)
(1.6)
Приклад 1. Знайти інтегральну функцію сумісного розподілу системи випадкових величин![]() , якщо відома густина сумісного розподілу
, якщо відома густина сумісного розподілу
![]() .
.
Розв’язування. За формулою (1.6)
![]()
![]()
![]() .
.
Враховуючи , що ![]() (властивість 3), для густини сумісного розподілу
(властивість 3), для густини сумісного розподілу ![]() можна записати рівність нормування
можна записати рівність нормування
![]() .
.
Ймовірність попадання випадкової точки ![]() у довільну область (рис.1.3) обчислюється за формулою
у довільну область (рис.1.3) обчислюється за формулою
![]() ,(1.7)
,(1.7)
яка одразу слідує з означення подвійного інтеграла
Приклад 1.5. Система випадкових величин ![]() задана густиною сумісного розподілу
задана густиною сумісного розподілу
![]() .
.
Знайти ймовірність попадання випадкової точки у прямокутник з вершинами ![]() ,
, ![]() ,
,![]() ,
,![]() .
.
Розв’язування. За формулою (1.7)
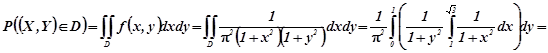
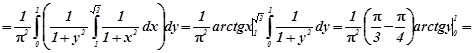 .
.
![]() .
.
Функції
![]() ,(1.8a)
,(1.8a)
![]() .(1.8b)
.(1.8b)
є інтегральними функціями розподілу компонент системи двох неперервних величин ![]() .
.
Приклад 1.6. Система випадкових величин ![]() задана густиною сумісного розподілу
задана густиною сумісного розподілу
![]() .
.
Знайти інтегральні функції компонент.
Розв’язування. За формулою (1.8а)
![]()
![]() .
.
За формулою (1.8б)
![]()
![]() .
.
За відомою густиною сумісного розподілу ймовірностей системи двох випадкових величин можна обчислити густину розподілу кожної її компоненти:
![]() (1.9a)
(1.9a)
![]() (1.9b)
(1.9b)
Доведення. З означення густини розподілу компоненти ![]() та з врахуванням (1.8a)
та з врахуванням (1.8a)
![]() .
.
Аналогічно для другої компоненти:
![]()
Приклад 1.7. Двовимірний вектор ![]() задан густиною сумісного розподілу
задан густиною сумісного розподілу
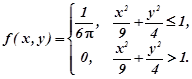
Знайти густини розподілів компонент X та Y.
Розв’язування. За формулою (1.9а) при ![]()
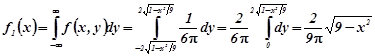 ,
,
і при ![]()
![]() . Отже,
. Отже,
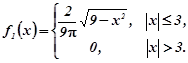
За формулою (1.9b) при ![]()
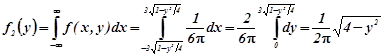 ,
,
і при ![]()
![]() . Отже,
. Отже,
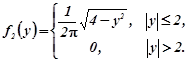
Дискретні випадкові двовимірні вектори однозначно визначаються також умовними розподілами компонент X,Y:
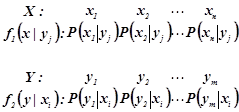 ,
,
![]() - умовна ймовірність події
- умовна ймовірність події ![]() за умови того, що подія
за умови того, що подія ![]() вже настала,
вже настала,
![]() - умовна ймовірність події
- умовна ймовірність події ![]() за умови, що подія
за умови, що подія ![]() вже настала.
вже настала.
За теоремою множення ймовірностей залежних подій
![]() ,(1.10а)
,(1.10а)
(![]() ),
),
![]() , (1.10b)
, (1.10b)
(![]() ).
).
Приклад 1.8. Необхідно обчислити умовні розподіли компоненти X системи випадкових подій ![]() із сумісним розподілом
із сумісним розподілом
y1 y2
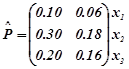
при ![]() .
.
Розв’язування. Імовірність події (![]() ) за формулою (1.1b).
) за формулою (1.1b).
![]()
За формулою (1.10а)
![]() ,
,
![]() ,
,
![]() .
.
Умовний розподіл компоненти X при ![]()
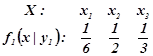
Імовірність події (![]() ) за формулою (1.1b).
) за формулою (1.1b).
![]() .
.
За формулою (1.10а)
![]() ,
,
![]() ,
,
![]() .
.
Умовний розподіл компоненти X при ![]()
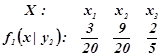 .
.
Імовірність події (![]() ) за формулою (1.1a)
) за формулою (1.1a)
![]() .
.
За формулою (1.10b)
![]() ,
,
![]() .
.
Умовний розподіл компоненти Y при ![]()
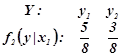 .
.
Імовірність події (![]() ) за формулою (1.1a)
) за формулою (1.1a)
![]() .
.
За формулою (1.10b)
![]() ,
,
![]() .
.
Умовний розподіл компоненти Y при ![]()
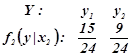
Імовірність події (![]() ) за формулою (1.1a)
) за формулою (1.1a)
![]() .
.
За формулою (1.10b)
![]() ,
,
![]() .
.
Умовний розподіл компоненти Y при ![]()
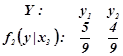 .
.
Умовні густини розподілу компонент системи двох неперервних випадкових величин ![]() визначаються рівностями
визначаються рівностями
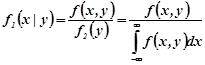 ,(1.11a)
,(1.11a)
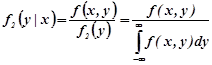 ,(1.11b)
,(1.11b)
![]() - умовна густина розподілу ймовірності компоненти X при фіксованому значенню
- умовна густина розподілу ймовірності компоненти X при фіксованому значенню ![]() ,
, ![]() - умовна густина розподілу ймовірності компоненти Y при фіксованому значенню
- умовна густина розподілу ймовірності компоненти Y при фіксованому значенню ![]() .
.
Приклад 1.9. Двовимірний вектор ![]() заданий густиною сумісного розподілу
заданий густиною сумісного розподілу
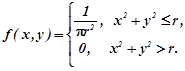 .
.
Знайти умовні розподіли компонент X та Y.
Розв’язування.![]() в крузі радіуса r і тому за формулою (1.11a)
в крузі радіуса r і тому за формулою (1.11a)
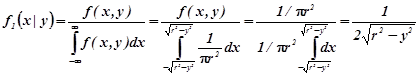
при ![]() і
і
![]() при
при ![]() .
.
У підсумку
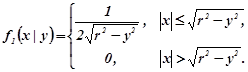
Аналогічно за формулою (1.11b)
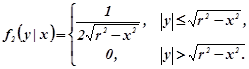
Як і будь-які інші густини розподілу, умовні ймовірності мають такі властивості
![]()
![]() ,
,
![]()
![]() .
.
Дві випадкові величини є незалежними, якщо закон розподілу однієї з них не залежить від значення іншої. Умовні розподіли незалежних величин дорівнюють їх розподілам:
![]()
для неперервних величин і
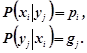 .
.
для дискретних випадкових величин.
Необхідною та достатньою умовою незалежності випадкових величин є
![]() ,(1.12а)
,(1.12а)
або, як наслідок,
![]() .(1.12b)
.(1.12b)
Похожие работы
... , . . Для опису зв'язків, що існують між проекціями випадкового вектора (x,h), крім коваріації можна використовувати числові характеристики умовних законів розподілу , . Умовним середнім значенням і умовною дисперсією випадкової величини x за умови h =y називаються величини: , . Аналогічно визначаються характеристики і . Для опису випадкового вектора також вводять початкові і ...
... вибірка із незалежних реалізацій БВВ , яка в подальшому використовується для побудови ВЕ із необхідними ймовірнісними характеристиками. При моделюванні на ЕОМ складних ВЕ, зокрема, випадкової величини (ВВ) або випадкового процесу (ВП) з заданими ймовірнісними характеристиками розглядається складний випадковий експеримент, що полягає в проведенні раз описаного вище найпростішого експерименту. ...
... ідністю варіювати значення ціни як безперервної випадкової величини. З курсу математичної статистики відомо, що математичне очікування нормально розподіленої випадкової величини можна представити у вигляді: (1.1) Практичне застосування даної формули при оцінці ризику в ціноутворенні вимагає її спрощення. Не утрудняючи читача відомими [1,3], але громіздкими перетвореннями одержуємо: ...
... 9 - 1 Імовірність 0,05 0,95 Математичне сподівання виграшу за один постріл подається у вигляді mx=9*0,05 + (-1)*0,95=-0,5. Перевіримо якість випадкових чисел, наведених у табл.Д1. ([3] Таблиця випадкових цифр). Для цього, склавши імітаційну модель гри, математичне сподівання виграшу оцінюватимемо за допомогою середнього арифметичного значення виграшу 440 пострілів. Умовимося, що ...






0 комментариев