Навигация
Числові характеристики системи випадкових величин та їх граничні теореми
1. Кореляційний момент, коефіцієнт кореляції
Кореляційним моментом (коваріацією) випадкових величин ![]() і
і ![]() називається математичне сподівання добутку відповідних ним центрованих величин:
називається математичне сподівання добутку відповідних ним центрованих величин:
![]() . (1)
. (1)
Властивості коваріації:
| 1. | ||
| 2. | ||
| 3. |
Перші дві з них очевидні, остання доводиться також легко:
![]()
Коефіцієнтом кореляції називається кореляційний момент нормованої випадкової величини:
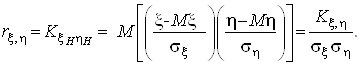
Теорема. Для будь-яких випадкових величин ![]() ,
, ![]() коефіцієнт кореляції
коефіцієнт кореляції ![]() причому знак рівності можливий тоді і тільки тоді, коли
причому знак рівності можливий тоді і тільки тоді, коли ![]() і
і ![]() з імовірністю 1 пов'язані лінійно.
з імовірністю 1 пов'язані лінійно.
Доведення. Обчислимо дисперсію лінійної комбінації випадкових величин ![]() і
і ![]() з довільним коефіцієнтом
з довільним коефіцієнтом ![]() та врахуємо, що з властивостей дисперсії вона є невід'ємною.
та врахуємо, що з властивостей дисперсії вона є невід'ємною.
При цьому отримаємо невід’ємну квадратичну форму відносно змінної ![]() з невід’ємним коефіцієнтом при
з невід’ємним коефіцієнтом при ![]() .
.
![]()
Це можливо лише за умови, що її дискримінант ![]() . З урахуванням визначення (1) цю нерівність можна переписати у вигляді:
. З урахуванням визначення (1) цю нерівність можна переписати у вигляді:
![]()
або
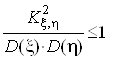
або мовою середніх квадратичних відхилень випадкових величин
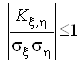 .
.
Тобто
![]()
Доведемо тепер другу частину теореми: ![]() тоді і тільки тоді, коли
тоді і тільки тоді, коли ![]() і
і ![]() з імовірністю 1 пов'язані лінійно.
з імовірністю 1 пов'язані лінійно.
Необхідність:
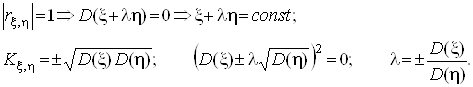
Достатність:
![]() ,
,  ,
, ![]() ,
,
![]() ,
, 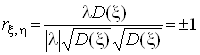 .
.
Випадкові величини x,h називаються некорельованими, якщо їх коваріація дорівнює нулю. Якщо випадкові величини x, h незалежні, то вони некорельовані.
![]() .
.
Зворотне твердження, взагалі кажучи, не має місця.
Наприклад,
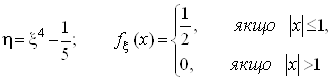 .
.
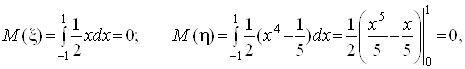
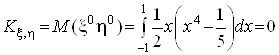 .
.
Для опису зв'язків, що існують між проекціями випадкового вектора (x,h), крім коваріації ![]() можна використовувати числові характеристики умовних законів розподілу
можна використовувати числові характеристики умовних законів розподілу ![]() ,
, ![]() .
.
Умовним середнім значенням ![]() і умовною дисперсією
і умовною дисперсією ![]() випадкової величини x за умови h =y називаються величини:
випадкової величини x за умови h =y називаються величини:
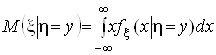 ,
,
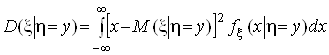 .
.
Аналогічно визначаються характеристики ![]() і
і ![]() .
.
Для опису випадкового вектора також вводять початкові і центральні моменти:
![]() ,
, ![]() .
.
Похожие работы
... рівність нормування . Ймовірність попадання випадкової точки у довільну область (рис.1.3) обчислюється за формулою ,(1.7) яка одразу слідує з означення подвійного інтеграла Приклад 1.5. Система випадкових величин задана густиною сумісного розподілу . Знайти ймовірність попадання випадкової точки у прямокутник з вершинами , ,,. Розв’язування. За формулою (1.7) . . ...
... ТЕОРІЇ ЙМОВІРНОСТЕЙ 1. Поняття та закон розподілу системи випадкових величин До цього часу ми розглядали одномірну випадкову величину X. Однак в сучасній теорії математичної обробки результатів багаторазових повторних геодезичних вимірювань використовують багатомірні випадкові величини. Багатомірна випадкова величина може складатися із декількох компонентів і бути двомірною, тримірною і так ...
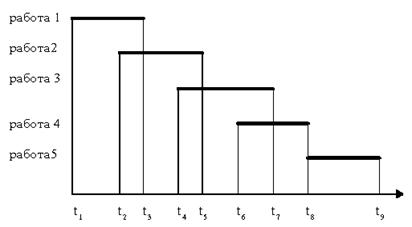
... і провести моделювання за початковими даними; · розробити програмне забезпечення для статистичного моделювання сітьового графіка за початковими даними; · зробити висновки по роботі та досягнутим результатам. 1 ЗАГАЛЬНА ХАРАКТЕРИСТИКА ПРЕДМЕТНОЇ ОБЛАСТІ 1.1 Дослідження процесу побудови судна 1.1.1 Аналіз процесу побудови судна як об’єкта ...
... часу електромашинного підсилювача Кп = 20 – коефіцієнт підсилення Отже передаточна функція ССП (без тахогенератора) буде мати такий вигляд: Kp(P) = Формалізована модель дослідження стійкості та якості перехідних процесів слідкувальної системи Формалізація приведення інформації зв’язаної з виділеними властивостями, до вибраної форми. внутрішні впливи; зовнішні впливи. ...

0 комментариев