Характеристики системи двох випадкових величин

2. Характеристики системи двох випадкових величин

 

Система двох випадкових величин  з достатньою точністю може характеризуватися початковими та центральними моментами компонент порядку , які є числами і тому називаються чисельними характеристиками, і умовними початковими та центральними моментами компонент порядку , які є функціями можливих значень компонент.

Початкові та центральні моменти означаються рівностями

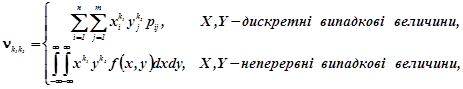(2.1а)

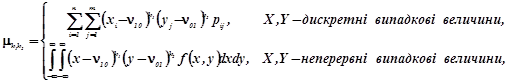(2.1б)

Найбільш важливими серед них є математичне сподівання компонент, дисперсії компонент та кореляційний момент.

Математичні сподівання компонент означаються так:

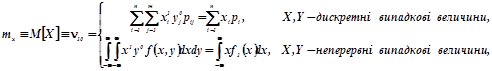(2.2а)

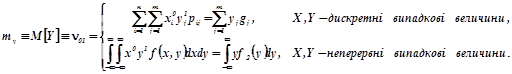(2.2б)

З використанням математичних сподівань компонент початкові та центральні моменти системи двох випадкових величин можна означити більш зручним способом:

,(2.3а)

,(2.3б)

(- центровані компоненти);

Дисперсії компонент означаються тотожностями

,(2.4а)

;(2.4б)

Кореляційний момент характеризує лінійний зв’язок між випадковими величинами. Він означається як центральний момент  і позначається :

,(2.5)

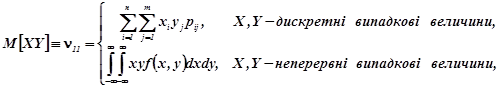(2.6)

Кореляційний момент часто називають коваріацією і позначається .

З використанням кореляційного моменту і коефіцієнта кореляції 3 –у властивість дисперсії (3.3.2.7) можна узагальнити на випадок суми (різниці) довільних випадкових величин:

.(2.7)

Доведення.

.

.

Для незалежних випадкових величин кореляційний момент дорівнює нулю:

.

Доведення.

.

Абсолютна величина кореляційного моменту випадкових величин не перевищує середньогеометричного значення дисперсій:

(2.8)

Доведення. Дисперсія випадкової величини  дорівнює

.(1*)

Дійсно:

,

,

.

За означенням дисперсія невід’ємна, тому з (1*)

звідки

.(2*)

Аналогічно, дисперсія випадкової величини дорівнює

,

звідки

.(3*)

Нерівності (2*) та (3*) рівносильні одній нерівності

=.

З означення кореляційного моменту слідує, що його розмірність дорівнює добутку розмірностей випадкових величин. Іншими словами, величина (точніше, число, яке визначає цю величину) кореляційного моменту залежить від одиниць вимірювання випадкових величин. Цього недоліку немає коефіцієнт кореляції, який визначається відношенням кореляційного моменту випадкових величин і добутку середньоквадратичних відхилень компонент  та :

(2.9)

Абсолютна величина коефіцієнта кореляції не перевищує одиниці:

.(2.10)

Нерівність (2.10) очевидна, якщо розділити нерівність (2.8) на .

Дві випадкові величини X та Y називають корельованими, якщо їх коефіцієнт кореляції не дорівнює нулю і, відповідно, некорельованими, якщо коефіцієнт кореляції дорівнює нулю. Дві випадкові корельовані величини обов’язково залежні. (з умови  одразу слідує, що , а для незалежних величин кореляційний момент обов’язково дорівнює нулю). Залежні величини можуть бути як корельованими, так і некорельованими.

Приклад 2.1. Двовимірна випадкова величина  задана густиною сумісного розподілу:

.

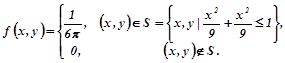Довести, що випадкові величини X та Y – залежні некорельовані величини.

Доведення. Необхідно довести, що та . З прикладу 1.7. густини розподілу компонент

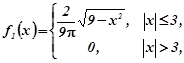
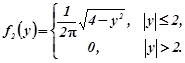
Видно, що , а це означає, що випадкові величини X та Y залежні. Математичні сподівання розподілів компонет і як симетричних розподілів. З врахуванням цього, з означення кореляційного моменту (2.5)

,

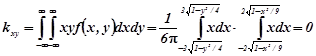(інтеграли від непарних функцій у симетричних границях дорівнюють нулю), а це і означає, що залежні випадкові величини X та Y некорельовані.

Незалежні випадкові величини обов’язково некорельовані. Некорельовані випадкові величини можуть бути як незалежними, так і залежними. Проте, некорельовані випадкові величині із нормальним розподілом у сукупності

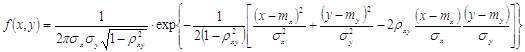(2.11)

обов’язково незалежні ( та - математичні сподівання випадкових величин  та .

Доведення Якщо (некорельованість випадкових величин), то (2.11) переходить у

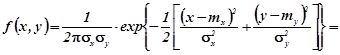
 (незалежність випадкових величин).

З використанням сумісного розподілу системи випадкових величин  та моментів можна строго довести властивості математичного сподівання випадкової величини (3.3.1.5) та (3.3.1.6)

Доведення 3-ї властивості математичного сподівання. За означенням для дискретних величини

.

Для неперервних величин

Доведення 4-ї властивості математичного сподівання. За означенням для дискретних величини

.

(враховано, що для незалежних подій )

Для неперервних величин

.

Умовні початкові та центральні моменти порядку k компонент означаються рівностями

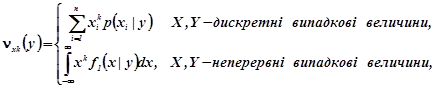(2.12a)

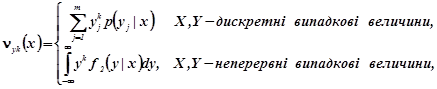(2.12b)

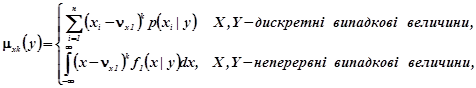(2.13а)

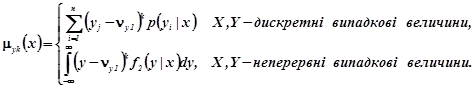(2.13b)

Найбільш важливими серед умовних моментів є умовні математичні сподівання компонент

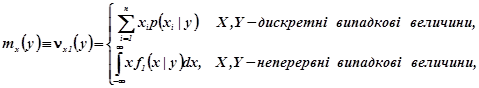(2.14а)

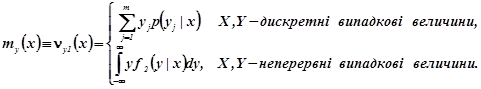(2.14b)

Умовні математичні сподівання компонент характеризують зв’язок між випадковими величинами Умовне математичне сподівання компоненти Y є функцією x і називається функцією регресії Y на X. Аналогічно, умовне математичне сподівання компоненти X є функцією y і називається функцією регресії X на Y.

Приклад 2.2. Дискретна випадкова величина задана сумісним розподілом

y₁=3y₂=6

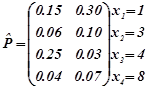
Необхідно обчислити функцію регресії Y на X та функцією регресії X на Y.

Розв’язування. За означенням (2.14b) регресія Y на X

. (1*)

За формулою (1.1a)

,

За формулою (1.10а)

 

, .

 

За формулою (1*)

.

Аналогічно для решти значень випадкової величини X .

, , ,

.

, , ,

.

, , ,

.

 

Отже, функція регресії Y на X

 

За означенням (2.14a) регресія X на Y

.(2*)

 

За формулою (1.1b)

.

За формулою (1.10b)

, , ,

.

За формулою (2*)

.

Аналогічно для іншого значення випадкової величини Y.

,

,,

, ,

.

Отже, функція регресії X на Y

 

.

 

Середньоквадратична регресія.

Нехай система двох залежних випадкових величин. І нехай необхідно дослідити залежність випадкових величин одне від одного. Досить часто випадкова величина Y апроксимується лінійною функцією випадкової величини X:

 

,(3.1)

 

a, b - параметри, які необхідно обчислити. Функція , яка забезпечує мінімум математичного сподівання

називається середньоквадратичною регресією Y на X. Дещо громізкими, але простими викладками можна довести ,що

.(3.2)

 

Доведення.

Точки мінімуму функції  знаходяться як розв’язок системи рівнянь

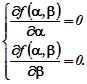
З врахуванням цього ця система рівнянь запишеться у вигляді

 

,

 

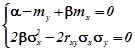розв’язок якої

, ,(3.3)

 

а значить середньоквадратична регресія Y на X остаточно запишеться у вигляді

(3.4)

 

Коефіцієнт називають коефіцієнтом середньоквадратичної регресії Y на X, а пряму

(3.5)

прямою середньої квадратичної регресії Y на X.

Мінімальне значення функції  (3.2)при значеннях a,b (3.3б)дорівнює  і називається залишковою дисперсією випадкової величини Y відносно величини X. Вона характеризує похибку апроксимації . При  залишкова дисперсія дорівнює 0. Це означає, що при таких значеннях коефіцієнта кореляції випадкові величини X та Y зв’язані лінійною функціональною залежністю. Значна величина залишкової дисперсії є ознакою того, апроксимація (3.1) є невдалою. У цьому випадку слід користуватися апроксимацією поліномами другої , третьої, і вище, степені.

Аналогічно, можна одержати пряму середньоквадратичної кореляції X на Y:

 

.(3.6)

(коефіцієнт - коефіцієнт середньоквадратичної регресії X на Y ,  - залишкова дисперсія випадкової величини X відносно величини Y. При обидві прямі регресії співпадають.

З рівностей (3.4) та (3.6) слідує, що обидві прямі проходять через точку . Цю точку називають центром сумісного розподілу двовимірної випадкової величини.

Лінійна кореляція нормальних величин

Якщо обидві функції регресій X на Y та Y на X є лінійними функціями, то говорять, що X та Y зв’язані лінійною кореляційною залежністю. Графіки лінійних регресій – прямі лінії, які співпадають з прямими середньоквадратичних регресій.

Якщо двовимірна випадкова величина (X ,Y) має нормальний закон розподілу у сукупності, то X та Y зв’язані лінійною кореляційною залежністю.

Доведення. Для спрощення густину нормального сумісного розподілу можна записати у вигляді

,

, , , .

Для знаходження регресії  необхідно знайти розподіл компоненти :

,

.

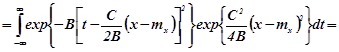
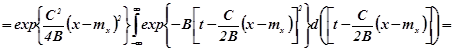
З врахуванням цього

.

,

,

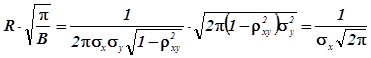Тому

.

Густина умовного розподілу компоненти

.

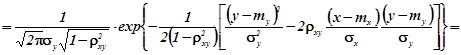
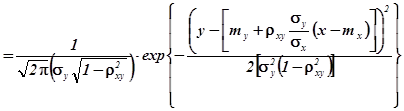Порівнюючи одержану густину умовного розподілу з густиною нормального розподілу можна зробити висновок, що умовний розподіл компоненти  є нормальним з математичним сподіванням (функцією регресії  на )

та умовною дисперсією

.

Аналогічно можна одержати функцію регресії  на

.

Видно, що обидві функцій регресій є лінійними, а значить кореляція між  та є лінійною,що й треба було довести. Крім того видно, що прямі регресій

співпадають з прямими середньоквадратичної регресії (3.5) та (3.6).