Навигация
Этот метод даёт возможность найти ориентировочное значение цены игры и приближённо вычислить оптимальные стратегии игроков
1. Этот метод даёт возможность найти ориентировочное значение цены игры и приближённо вычислить оптимальные стратегии игроков.
2. Сложность и объём вычислений сравнительно слабо возрастают по мере увеличения числа стратегий игроков (m и n).
Для рассмотренного алгоритма приведена реализация на языке Pascal (см. приложение).
§3. Монотонный итеративный алгоритм решения матричных игр
Предлагаемый для рассмотрения алгоритм реализуется только для одного игрока в отличие от первого, который работает для двух игроков. Алгоритм позволяет находить точно и приближенно оптимальную стратегию игрока 1 и значение цены игры n. С помощью алгоритма можно получить заданную точность решения, причём число шагов, необходимых для достижения результатов, слабо зависит от размерности матрицы выигрышей.
Особенность этого алгоритма в способности генерировать строго монотонно возрастающую последовательность оценок цены игры, что не свойственно ранее предлагаемому алгоритму.
Рассмотрим смешанное расширение ![]() =(X,Y,K) матричной игры ГА с матрицей А размера (m´n). Процесс разыгрывания игры состоит из нескольких шагов. Пусть каждый из игроков имеет конечное число стратегий.
=(X,Y,K) матричной игры ГА с матрицей А размера (m´n). Процесс разыгрывания игры состоит из нескольких шагов. Пусть каждый из игроков имеет конечное число стратегий.
Введём следующие обозначения:
аi – i-я строка матрицы выигрышей;
xN=(x1N,x2N,…,xmN) ÎX – m-мерный вектор, приближение оптимальной стратеги первого игрока на N-шаге (N-номер шага);
cN=(![]() ) –n-мерный вектор, определяющий средний накопленный выигрыш на N-шаге.
) –n-мерный вектор, определяющий средний накопленный выигрыш на N-шаге.
Зададим начальные условия. Пусть на 0-шаге с0=![]() , x0=(0,…, 1,…, 0), где 1 занимает i0-ю позицию.
, x0=(0,…, 1,…, 0), где 1 занимает i0-ю позицию.
Определим итеративный процесс следующим образом: по известным векторам xN-1, cN-1 находим векторы xN и cN , которые вычисляются по следующим формулам:
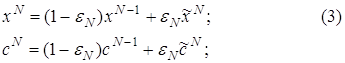
![]() где параметр 0£eN£1, а векторы
где параметр 0£eN£1, а векторы ![]() вводятся далее.
вводятся далее.
Как отмечалось, вектор сN определяет средний накопленный выигрыш игрока 1 на N шаге. Компоненты этого вектора – это числа. В худшем случае игрок 1 может получить минимальное из этих чисел. Примем его за нижнюю оценку цену игры, которую обозначим:
![]() . (4)
. (4)
Запомним множество
индексов JN-1=(![]() ), (k<n), на которых будет достигается этот минимум, т. е.
), (k<n), на которых будет достигается этот минимум, т. е.
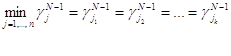 .
.
Далее рассмотрим подыгру
ГN игрыГА с матрицей выигрышей АN={![]() }, i=1,…,m, jN-1ÎJN-1. Матрица выигрышей состоит из столбцов данной матрицы, номера которых определяются множеством индексов JN-1. В этой подыгре ГN находим одну из оптимальных смешанных стратегий игрока 1:
}, i=1,…,m, jN-1ÎJN-1. Матрица выигрышей состоит из столбцов данной матрицы, номера которых определяются множеством индексов JN-1. В этой подыгре ГN находим одну из оптимальных смешанных стратегий игрока 1: ![]() .
.
После нахождения ![]() , находим вектор
, находим вектор ![]() по правилу:
по правилу:
![]() .
.
И рассмотрим игру (2´n), в которой у игрока 1 две чистые стратегии, а у игрока 2 – n чистых стратегий. Эта игра задаётся матрицей 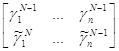 , решая которую, находим вероятность использования игроком 1 своей стратегии. Это даёт нам коэффициент eN.
, решая которую, находим вероятность использования игроком 1 своей стратегии. Это даёт нам коэффициент eN.
Далее вычисляем xN, сN и переходим к следующему шагу. Процесс продолжаем до тех пор, пока не выполнится равенство eN=0, потому что по теореме о минимаксе ![]() , а их равенство (что и нужно) достигается в этом случае, или пока не будет достигнута требуемая точность вычислений.
, а их равенство (что и нужно) достигается в этом случае, или пока не будет достигнута требуемая точность вычислений.
Сходимость алгоритма гарантируется теоремой.
Теорема. Пусть {xN}, {nN} – последовательности, определяемые равенствами (3), (4) . Тогда справедливы следующие утверждения:
1. ![]() т. е. последовательность {nN-1} строго монотонно возрастает.
т. е. последовательность {nN-1} строго монотонно возрастает.
2. ![]()
3. ![]() , где x*ÎX* – оптимальная стратегия игрока 1.
, где x*ÎX* – оптимальная стратегия игрока 1.
Доказательства этой теоремы достаточно рутинно. Его можно посмотреть в [15].
Рассмотрим применение этого алгоритма к решению конкретной задачи.
Пример. Решить игру с матрицей А=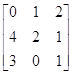 .
.
Итерация 0. 1. Пусть игрок 1 выбрал свою 1-ю стратегию, т. е. А0=[0, 1, 2]. Тогда за начальные условия примем следующие: x0=(1, 0, 0) – приближение оптимальной стратегии игрока 1; c0=a1=(0, 1, 2) – возможный выигрыш игрока 1.
Найдём множество индексов ![]() , на которых игрок 1 может получить, в худшем случае, наименьший выигрыш:
, на которых игрок 1 может получить, в худшем случае, наименьший выигрыш: ![]() , значит множество индексов J0={1}. Для этого индекса выигрыш равен 0. Это есть значение нижней оценки цены игры, т. е.
, значит множество индексов J0={1}. Для этого индекса выигрыш равен 0. Это есть значение нижней оценки цены игры, т. е. ![]() .
.
2. На этом шаге определим, пользуясь начальными значениями, компоненты векторов ![]() . Для этого рассмотрим подыгру
. Для этого рассмотрим подыгру 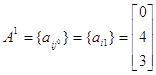 . Для этой подыгры оптимальной стратегией игрока 1 будет его 2-ая стратегия, так как она принесёт ему наибольший выигрыш.
. Для этой подыгры оптимальной стратегией игрока 1 будет его 2-ая стратегия, так как она принесёт ему наибольший выигрыш.
Обозначим её через ![]() :
: ![]() =(0, 1, 0). Зная
=(0, 1, 0). Зная ![]() , можем вычислить
, можем вычислить ![]() =0а1+1а2+0а3=а2=(4, 2, 1).
=0а1+1а2+0а3=а2=(4, 2, 1).
3. Найдём e1. Для этого рассмотрим подыгру (2´3) с матрицей 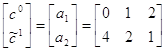 . Решая матрицу графическим способом, получаем, что e1=1/2.
. Решая матрицу графическим способом, получаем, что e1=1/2.
4. Проведённые вычисления позволяют найти значения векторов x1, c1:
x1=1/2x0+1/2 ![]() =1/2(1, 0, 0)+1/2(0, 1, 0)=(1/2, 1/2, 0);
=1/2(1, 0, 0)+1/2(0, 1, 0)=(1/2, 1/2, 0);
c1=1/2c0+1/2 ![]() =1/2(0, 1, 2)+1/2(4, 2, 1)=(2, 3/2, 3/2).
=1/2(0, 1, 2)+1/2(4, 2, 1)=(2, 3/2, 3/2).
Итерация 1. Так как e1 не равно 0, то процесс продолжается дальше. Теперь за начальные условия примем найденные значения векторов x1, c1. С их помощью вычисляем ![]() , которые с большей точностью будут близки к истинным оптимальным стратегиям игрока 1.
, которые с большей точностью будут близки к истинным оптимальным стратегиям игрока 1.
1. Итак, пусть x1=(1/2, 1/2, 0), c1=(2, 3/2, 3/2).
Найдём множество индексов ![]() , на которых игрок 1 может получить наименьший выигрыш:
, на которых игрок 1 может получить наименьший выигрыш: ![]() , значит, J1={2,3}. Для этих индексов выигрыш равен 3/2. Это есть значение нижней оценки цены игры, т. е.
, значит, J1={2,3}. Для этих индексов выигрыш равен 3/2. Это есть значение нижней оценки цены игры, т. е. ![]() . Заметим, что
. Заметим, что ![]() .
.
2. Далее найдём компоненты векторов ![]() . Для этого рассмотрим подыгру
. Для этого рассмотрим подыгру 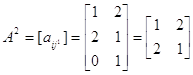 . В силу симметричности матрицы ее решением будет вектор (1/2, 1/2), т. е.
. В силу симметричности матрицы ее решением будет вектор (1/2, 1/2), т. е. ![]() 1/2a1+1/2a2+0a3=
1/2a1+1/2a2+0a3=
=(4/2, 3/2, 3/2).
3. Вычислим коэффициент e2. Для этого решим подыгру (2´3):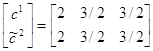 . Стратегии игроков совпадают, поэтому e2=0. В этом случае цена игры совпадает со своим нижним значением, т. е.
. Стратегии игроков совпадают, поэтому e2=0. В этом случае цена игры совпадает со своим нижним значением, т. е.![]() . Возвращаемся к предыдущему шагу.
. Возвращаемся к предыдущему шагу.
Итак, оптимальной стратегией игрока 1 является x*=x1=(1/2, 1/2, 0) и ![]() .Задача решена.
.Задача решена.
На первый взгляд алгоритм практически трудно реализовать, так как не известно, какого размера будет получена матрица для подыгры ГN. Но на самом деле с вероятностью 1 на каждом шаге придётся решать подыгру размера не больше чем m´2.[9]
Инженерами-программистами алгоритм был реализован на языке программирования Фортран-IV. Вычислительные эксперименты, проведённые на ЭЦВМ ЕС-1030, показали, что для игр размерности от 25´25 до 100´100, элементы, матрицы выигрышей которых были заполнены случайными числами, алгоритм позволяет найти искомое приближение за 100-1000 итераций, причём их число слабо зависит от размера матрицы. Для решения одной задачи машина затрачивает не дольше 8 минут. Ими же были разработаны различные модификации алгоритма. [9]
Приложение
В приложении приведена реализация итеративного метода Брауна-Робинсона решения матричных игр на языке программирования Turbo Pascal 7.0.
Пользователь вводит матрицу выигрышей размера m×n, где m≥3, n≥3.
Далее машина запрашивает информацию о том, кто из игроков начинает игру, какую стратегию он выбирает и количество итераций.
На дисплее выводится таблица разыгрываний игры за определённое число итераций.
program br;
uses crt;
const matr1:array[1..3,1..3] of byte=((0,4,2),
(3,1,0),
(1,2,3)); {Начальная матрица}
var
matr:array [1..10,1..10] of integer; {Матрица, введенная пользователем}
win_one:array[0..150,1..10] of word; {Массив для выигрышей игр.1}
win_two:array[0..150,1..10] of word; {Массив для выигрышей игр.2}
max,min:integer;
a,i,j,m,n,pl,st,st1,st2,kl:byte;
nol,otr:boolean;
function igr_one:byte; {Функция определения следующего}
var a1,a2,max:integer; {хода для игрока 1}
begin
max:=win_one[a,1];
igr_one:=1;
if pl=1 then a2:=m else a2:=n;
for a1:=1 to a2 do if win_one[a,a1]>max then begin
max:=win_one[a,a1];
igr_one:=a1;
end;
end;
function igr_two:byte; {Функция определения следующего}
var a1,a2,min:integer; {хода для игрока 2}
begin
min:=win_two[a,1];
igr_two:=1;
if pl=1 then a2:=n else a2:=m;
for a1:=1 to a2 do if win_two[a,a1]<min then begin
min:=win_two[a,a1];
igr_two:=a1;
end;
end;
begin
clrscr;
writeln ('Итеративный метод Брауна-Робинсона.');
writeln('Матрица пользователя? (y/n)');
if (readkey='y')or(readkey='Y') then begin {Матрица из памяти или вводит пользователь}
write ('Введите размеры матрицы:');
readln(n,m); {Ввод количества строк и столбцов}
writeln('Введите ',n,' строки по ',m,' элементов:');
nol:=true;
otr:=false;
min:=0;
for j:=1 to n do for i:=1 to m do begin {Ввод элементов матрицы}
read(matr[i,j]);
if matr[i,j]<>0 then nol:=false; {Установка флага, что не все элементы равны 0}
if matr[i,j]<0 then otr:=true; {Установка флага наличия отрицательных элементов}
if matr[i,j]<min then min:=matr[i,j];{Определение минимального элемента}
end
end else begin {Иначе берем матрицу из константы}
n:=3;m:=3;
for i:=1 to m do for j:=1 to n do matr[i,j]:=matr1[i,j];
end;
clrscr;
writeln ('Итеративный метод Брауна-Робинсона.');
if nol then writeln('Все элементы матрицы равны 0!') else begin {если установлен флаг нуля, то алгоритм не работает}
if otr then for j:=1 to n do for i:=1 to m do matr[i,j]:=matr[i,j]-min;{если есть отрицательные элементы,}
writeln('Начальная матрица:'); {Вывод окончательной матрицы}
for j:=1 to n do begin
for i:=1 to m do write(matr[i,j]:4);
writeln;
end;
write('Какой игрок начнет игру? '); {Вод стартовых значений}
readln(pl);
write('Какую стратегию выберет ',pl,' игрок? ');
readln(st);
write('Количество итераций? ');
readln(kl);
a:=1; {заглавие таблицы}
writeln(' № стр. выигрыш 1-го игр. стр. выигрыш 2-го игр. V W Y');
repeat
write(a:2,st:6,' '); {формирование таблицы: номер итерации, стратегия 1игр.}
if pl=2 then begin
for i:=1 to n do begin
win_one[a,i]:=matr[st,i]+win_one[a-1,i];{формирование матрицы выигрышей 1 игр.}
write(win_one[a,i]:4); {вывод на экран}
end;
st1:=igr_one; {определение ответной стратегии 2 игр.}
gotoxy(32,wherey);
write(st1:10,' '); {вывод на экран}
for i:=1 to m do begin
win_two[a,i]:=matr[i,st1]+win_two[a-1,i]; {формирование матрицы выигрышей 2 игр.}
write(win_two[a,i]:4); {вывод на экран}
end;
gotoxy(64,wherey);
write(win_one[a,st1]:4); {вывод наибольшего суммарного выигрыша 1 игр.}
st:=igr_two; {определение ответной стратегии 1 игр.}
write(win_two[a,st]:4); {вывод наибольшего суммарного выигрыша 2 игр.}
write((win_one[a,st1]+win_two[a,st])/(a*2):6:2);{приближенное значение цены игры}
end
else
begin
for i:=1 to m do begin
win_one[a,i]:=matr[i,st]+win_one[a-1,i];{формирование матрицы выигрышей 1 игр.}
write(win_one[a,i]:4);
end;
st1:=igr_one; {определение ответной стратегии 2 игр.}
gotoxy(32,wherey);
write(st1:10,' ');
for i:=1 to n do begin
win_two[a,i]:=matr[st1,i]+win_two[a-1,i];{формирование матрицы выигрышей 2 игр.}
write(win_two[a,i]:4);
end;
gotoxy(64,wherey);
write(win_one[a,st1]:4); {вывод наибольшего суммарного выигрыша 1 игр.}
st:=igr_two; {определение ответной стратегии 1 игр.}
write(win_two[a,st]:4); {вывод наибольшего суммарного выигрыша 2 игр.}
write((win_one[a,st1]+win_two[a,st])/(a*2):6:2);{приближенное значение цены игры}
end;
a:=a+1; {увеличение счетчика итераций}
writeln;
until a=kl+1;
end;
readln;
readln;
end.
Список литературы
1. Беленький В.З. Итеративные методы в теории игр и программировании. М.: «Наука», 1977
2. Блекуэлл Д.А. Теория игр и статистических решений. М., Изд. иностранной литературы, 1958
3. Вентцель Е.С. Элементы теории игр. М., Физматгиз, 1961
4. Вилкас Э.И. Оптимальность в играх и решениях. М.: «Наука», 1986
5. Воробьёв И.Н. Математическая теория игр. М.: «Знание», 1976
6. Давыдов Э.Г. Методы и модели теории антагонистических игр. М.: «Высшая школа», 1990
7. Дрешер М. Стратегические игры. Теория и приложения. М., 1964
8. Исследование операций в экономике / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман. М.: «Банки и биржи», Юнити, 1997
9. Итеративный алгоритм решения матричных игр// Доклады Академии наук СССР, том 238, №3, 1978
10. Карлин С. Математические методы в теории игр, программировании и экономике. М.: «Мир», 1964
11. Крапивин В.Ф. Теоретико-игровые методы синтеза сложных систем в конфликтных ситуациях. М.: «Советское радио», 1972
12. Крушевский А.В. Теория игр: [Учебное пособие для вузов]. Киев: «Вища школа», 1977
13. Льюис Р., Райфа Х. Игры и решения. М.,1961
14. Морозов В.В., Старёв А.Г., Фёдоров В.В. Исследование операций в задачах и упражнениях. М.: «Высшая школа», 1996
15. Матричные игры. [Сборник переводов]. Под ред. Воробьёва И.Н. М., Физматгиз, 1961
16. Оуэн Г. Теория игр. [Учебное пособие]. М.: «Мир», 1973
17. Петросян Л.А., Зенкевич Н.А., Семен Е.А. Теория игр. М., 1989
18. Школьная энциклопедия математика. Ред. С. М. Никольский, М.: 1996, с. 380
Похожие работы
ные приравняем к нулю, найдём оптимальное количество вложенного труда Задание №2 2. Даны зависимости спроса D=200-2p и предложения S=100+3p от цены. Найдите равновесную цену, цену при которой выручка максимальна и эту максимальную выручку. Решение: Равновесная цена находится путём приравиевания спроса и предложения, т.е. 200-2p=100+3p; p*=20 – равновесная цена. Найдём ...
р, на основе недостаточных данных) можно интерпретировать как конфликт принимающего решения субъекта с природой. Поэтому Теория игр рассматривается также как теория принятия оптимальных решений в условиях неопределённости. Она позволяет математизировать некоторые важные аспекты принятия решений в технике, сельском хозяйстве, медицине и социологии. Перспективен подход с позиций Теории игр к ...
... материало-, энерго-, фондо- и трудоёмкости продукции. Особую роль играют показатели водоёмкости и транспортабельности продукции. Технико-экономические показатели анализов территориальной организации народного хозяйства рассчитывают определением размеров соответствующих затрат на производство единицы продукции. Затраты отдельных ресурсов и выпуск новой продукции целесообразно определять в ...
... , следование которым позволяет организации постоянно добиваться своих целей. В дополнение к потенциалу, обеспечивающему будущее функционирование организации, другим конечным продуктом стратегического управления являются её структура и изменения, обеспечивающие чувствительность к изменениям во внешних условиях. В предпринимательской фирме это требует наличия управленческой способности замечать и ...
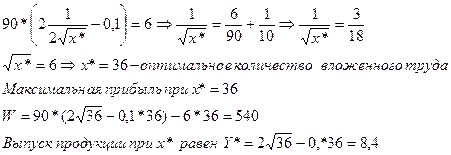
0 комментариев