Навигация
Решение систем линейных алгебраических уравнений. Методом Крамера. Методом Гаусса. Метод Жордана Гаусса. Метод Зейделя
2. Решение систем линейных алгебраических уравнений. Методом Крамера. Методом Гаусса. Метод Жордана Гаусса. Метод Зейделя
Решение систем линейных алгебраических уравнений – одна из основных задач вычислительной линейной алгебры. Хотя задача решения системы линейных уравнений сравнительно редко представляет самостоятельный интерес для приложений, от умения эффективно решать такие системы часто зависит сама возможность математического моделирования самых разнообразных процессов с применением ЭВМ. Значительная часть численных методов решения различных (в особенности – нелинейных) задач включает в себя решение систем линейных уравнений как элементарный шаг соответствующего алгоритма. Одна из трудностей практического решения систем большой размерности связанна с ограниченностью оперативной памяти ЭВМ. Хотя объем оперативной памяти вновь создаваемых вычислительных машин растет очень быстро, тем не менее, еще быстрее возрастают потребности практики в решении задач все большей размерности. В значительной степени ограничения на размерность решаемых систем можно снять, если использовать для хранения матрицы внешние запоминающие устройства. Однако в этом случае многократно возрастают как затраты машинного времени, так и сложность соответствующих алгоритмов. Поэтому при создании вычислительных алгоритмов линейной алгебры большое внимание уделяют способам компактного размещения элементов матриц в памяти ЭВМ.
К счастью, приложения очень часто приводят к матрицам, в которых число ненулевых элементов много меньше общего числа элементов матрицы. Такие матрицы принято называть разреженными. Одним из основных источников разреженных матриц являются математические модели технических устройств, состоящих из большого числа элементов, связи между которыми локальны. Простейшие примеры таких устройств – сложные строительные конструкции и большие электрические цепи.
Известны примеры решенных в последние годы задач, где число неизвестных достигало сотен тысяч. Естественно, это было бы невозможно, если бы соответствующие матрицы не являлись разреженными (матрица системы из 100 тыс. уравнений в формате двойной точности заняла бы около 75 Гбайт).
Методом Крамера. Известно, что используя матрицы мы можем решать различные системы уравнений, причем эти системы могут быть какой угодно величины и иметь сколько угодно переменных. С помощью нескольких выводов и формул решение огромных систем уравнений становится довольно быстрым и более легким.
В частности, я опишу методы Крамера и Гаусса. Наилегчайшим способом является метод Крамера (для меня ), или как его еще называют – формула Крамера. Итак, допустим, что мы имеем какую-либо систему уравнений
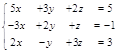 ,
,
в виде матрицы эту систему можно записать таким образом:
A = 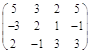 ,
,
где ответы будут уравнений будут находится в последнем столбце. Теперь мы введем понятие основного определителя; в данном случае он будет выглядеть таким образом:
![]() =
= 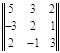 .
.
Основным определителем как вы уже заметили является матрица составленная из коэффициентов стоящих при переменных. Они также идут в порядке столбцов, т. е. в первом столбце стоят коэффициенты, которые находятся при x, во втором столбце при y, и так далее. Это очень важно, ибо в следующих действиях мы будем заменять каждый столбец коэффициентов при переменной на столбец ответов уравнений. Итак, как я уже говорил, мы заменяем столбец при первой переменной на столбец ответов, затем при второй, конечно это все зависит от того, сколько переменных нам нужно найти.
![]() 1 =
1 = 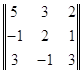 ,
, ![]() 2 =
2 = 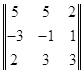 ,
, ![]() 3 =
3 = 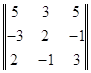 .
.
Затем нужно найти определители ![]() 1 ,
1 , ![]() 2 ,
2 , ![]() 3 . Как находится определитель третьего порядка вы уже знаете. А вот здесь мы и применяем правило Крамера. Оно выглядит так:
3 . Как находится определитель третьего порядка вы уже знаете. А вот здесь мы и применяем правило Крамера. Оно выглядит так:
x1 = ![]() , x2 =
, x2 = ![]() , x3 =
, x3 = ![]()
– для данного случая, а в общем виде оно выглядит следующим образом: xi = ![]() . Определитель составленный из коэффициентов при неизвестных, называется определителем системы.
. Определитель составленный из коэффициентов при неизвестных, называется определителем системы.
Вычисления с помощью метода Гаусса заключаются в последовательном исключении неизвестных из системы для преобразования ее к эквивалентной системе с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода.
Схема единственного деления. Рассмотрим сначала простейший вариант метода Гаусса, называемый схемой единственного деления.
Прямой ход состоит из n - 1 шагов исключения.
1-й шаг. Целью этого шага является исключение неизвестного x1 из уравнений с номерами i = 2, 3, …, n. Предположим, что коэффициент a11 ¹ 0. Будем называть его главным элементом 1-го шага.
Найдем величины
qi1 = ai1/a11 (i = 2, 3, …, n),
называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, …, n-го уравнений системы первое уравнение, умноженное соответственно на q21, q31, …, qn1. Это позволит обратить в ноль коэффициенты при x1 во всех уравнениях, кроме первого. В результате получим эквивалентную систему
a11x1 + a12x2 + a13x3 + … + a1nxn = b1 ,
a22(1)x2 + a23(1)x3 + … + a2n(1)xn = b2(1) ,
a32(1)x2 + a33(1)x3 + … + a3n(1)xn = b3(1) ,
an2(1)x2 + an3(1)x3 + … + ann(1)xn = bn(1).
в которой aij(1) и bij(1) вычисляются по формулам
aij(1) = aij − qi1a1j , bi(1) = bi − qi1b1.
2-й шаг. Целью этого шага является исключение неизвестного x2 из уравнений с номерами i = 3, 4, …, n. Пусть a22(1) ≠ 0, где a22(1) – коэффициент, называемый главным (или ведущим) элементом 2-го шага. Вычислим множители 2-го шага
qi2 = ai2(1) / a22(1) (i = 3, 4, …, n)
и вычтем последовательно из третьего, четвертого, …, n-го уравнения системы второе уравнение, умноженное соответственно на q32, q42, …, qm2. В результате получим систему
a11x1 + a12x2 + a13x3 +… + a1nxn = b1,
a22(1)x2 + a23(1)x3 +… + a2n(1) = b2(1),
a33(2)x3 +… + a3n(2)xn = b3(2),
an3(2)x3 +… + ann(2)xn = bn(2).
Здесь коэффициенты aij(2) и bij(2) вычисляются по формулам
aij(2) = aij(1) – qi2a2j(1) , bi(2) = bi(1) – qi2b2(1).
Аналогично проводятся остальные шаги. Опишем очередной k-й шаг.
k-й шаг. В предположении, что главный (ведущий) элемент k-го шага akk(k–1) отличен от нуля, вычислим множители k-го шага
qik = aik(k–1) / akk(k–1) (i = k + 1, …, n)
и вычтем последовательно из (k + 1)-го, …, n-го уравнений полученной на предыдущем шаге системы k-e уравнение, умноженное соответственно на
qk+1,k, qk+2,k, …, qnk.
После (n - 1)-го шага исключения получим систему уравнений
a11x1 +a12x2 +a13x3 +… +a1nxn =b1,
a22(1)x2 +a23(1)x3 +… +a2n(1)xn =b2(1),
a33(2)x3 +… +a3n(2)xn =b3(2),
ann(n–1)xn =bn(n–1).
матрица A(n-1) которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.
Обратный ход. Из последнего уравнения системы находим xn. Подставляя найденное значение xn в предпоследнее уравнение, получим xn–1. Осуществляя обратную подстановку, далее последовательно находим xn–1, xn–2, …, x1. Вычисления неизвестных здесь проводятся по формулам
xn = bn(n–1) / ann(n–1),
xk = (bn(k–1) – ak,k+1(k–1)xk+1 – – akn(k–1)xn) / akk(k–1), (k = n – 1, 1).
Необходимость выбора главных элементов. Заметим, что вычисление множителей, а также обратная подстановка требуют деления на главные элементы akk(k–1). Поэтому если один из главных элементов оказывыется равным нулю, то схема единственного деления не может быть реализована. Здравый смысл подсказывает, что и в ситуации, когда все главные элементы отличны от нуля, но среди них есть близкие к нулю, возможен неконтролируемый рост погрешности.
Метод Гаусса с выбором главного элемента по столбцу (схема частичного выбора). Описание метода. На k-м шаге прямого хода коэффициенты уравнений системы с номерами i = k + 1, …, n преобразуются по формулам
aij(k) = aij(k–1) − qikakj , bi(k) = bi(k–1) − qikbk(k–1) , i = k + 1, …, n.
Интуитивно ясно, что во избежание сильного роста коэффициентов системы и связанных с этим ошибок нельзя допускать появления больших множителей qik.
В методе Гаусса с выбором главного элементоа по столбцу гарантируется, что |qik| ≤ 1 для всех k = 1, 2, …, n – 1 и i = k + 1, …, n. Отличие этого варианта метода Гаусса от схемы единственного деления заключается в том, что на k-м шаге исключения в качестве главного элемента выбирают максимальный по модулю коэффициент aikk при неизвестной xk в уравнениях с номерами i = k + 1, …, n. Затем соответствующее выбранному коэффициенту уравнение с номером ik меняют местами с k-м уравнением системы для того, чтобы главный элемент занял место коэффициента akk(k-1). После этой перестановки исключение неизвестного xk производят, как в схеме единственного деления.
Метод Гаусса с выбором главного элемента по всей матрице (схема полного выбора). В этой схеме допускается нарушение естественного порядка исключения неизвестных.
На 1-м шаге метода среди элементов aij определяют максимальный по модулю элемент ai1j1. Первое уравнение системы и уравнение с номером i1 меняют местами. Далее стандартным образом производят исключение неизвестного xi1 из всех уравнений, кроме первого.
На k-м шаге метода среди коэффициентов aij(k–1) при неизвестных в уравнениях системы с номерами i = k, …, n выбирают максимальный по модулю коэффициент aikjk(k-1). Затем k-е уравнение и уравнение, содержащее найденный коэффициент, меняют местами и исключают неизвестное xjk из уравнений с номерами i = k + 1, …, n.
На этапе обратного хода неизвестные вычисляют в следующем порядке: xjn, xjn–1, …, xj1.
3. Метод Зейделя 3.2.1. Приведение системы к виду, удобному для итераций. Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений
Ax = b
с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду
x = Bx + c.
Здесь B – квадратная матрица с элементами bij (i, j = 1, 2, …, n), c – вектор-столбец с элементами cij (i = 1, 2, …, n).
В развернутой форме записи система имеет следующий вид:
x1 = b11x1 + b12x2 + b13x3 + … + b1nxn + c1
x2 = b21x1 + b22x2 + b23x3 + … + b2nxn + c2
xn = bn1x1 + bn2x2 + bn3x3 + … + bnnxn + cn
Вообще говоря, операция приведения системы к виду, удобному для итераций, не является простой и требует специальных знаний, а также существенного использования специфики системы.
Самый простой способ приведения системы к виду, удобному для итераций, состоит в следующем. Из первого уравнения системы выразим неизвестное x1:
x1 = a11–1 (b1 – a12x2 – a13x3 – … – a1nxn),
из второго уравнения – неизвестное x2:
x2 = a21–1 (b2 – a22x2 – a23x3 – … – a2nxn),
и т. д. В результате получим систему
x1 = b12x2 +b13x3 +… +b1,n–1xn–1 +b1nxn+c1 ,
x2 = b21x1 +b23x3 +… +b2,n–1xn–1 +b2nxn+c2 ,
x3 = b31x1 +b32x2 +… +b3,n–1xn–1 +b3nxn+c3 ,
xn = bn1x1 +bn2x2 +bn3x3 +… +bn,n–1xn–1 +cn ,
в которой на главной диагонали матрицы B находятся нулевые элементы. Остальные элементы выражаются по формулам
bij = –aij / aii, ci = bi / aii (i, j = 1, 2, …, n, j ≠ i)
Конечно, для возможности выполнения указанного преобразования необходимо, чтобы диагональные элементы матрицы A были ненулевыми.
Описание метода. Введем нижнюю и верхнюю треугольные матрицы
![]() 000…00b12b13…b1n
000…00b12b13…b1n
B1 =b2100…0B2 =00b23…b2n
b31b320…0, 000…b3n
bn1bn2bn3…0000…0
Заметим, что B = B1 + B2 и поэтому решение x исходной системы удовлетворяет равенству
x = B1x + B2 x + c.
Выберем начальное приближение x(0) = [x1(0), x2(0), …, xn(0)]T. Подставляя его в правую часть равенства при верхней треугольной матрице B2 и вычисляя полученное выражение, находим первое приближение
x(1) = B1x(0) + B2x(1)
Подставляя приближение x(1), получим
x(2) = B1x(1) + B2x(2)
Продолжая этот процесс далее, получим последовательность x(0), x(1), …, x(n), … приближений к вычисляемых по формуле
x(k+1) = B1(k+1) + B2(k) + c
или в развернутой форме записи
x1(k+1) =b12x2(k) +b13x2(k) +… +b1nxn(k) +c1 ,
x2(k+1) =b21x1(k+1) +b23x3(k) + … +b2nxn(k) +c2 ,
x3(k+1) =b31x1(k+1) +b32x2(k+1) +… +b3nxn(k) +c3 ,
xn(k+1) =bn1x1(k+1) +bn2x2(k+1) +bn3x3(k+1) +… +cn.
Объединив приведение системы к виду, удобному для итераций и метод Зейделя в одну формулу, получим
xi(k+1) = xi(k) – aii–1(∑j=1i–1 aijxj(k+1) + ∑j=1n aijxi(k) – bi).
Тогда достаточным условием сходимости метода Зейделя будет
∑j=1, j≠i n | aij | < | aii |
(условие доминирования диагонали).
Метод Зейделя иногда называют также методом Гаусса-Зейделя, процессом Либмана, методом последовательных замещений.
Похожие работы
... - в методе Ньютона наблюдается ускорение сходимости процесса приближений. 5. Метод касательных (метод Ньютона) Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f ¢(x) (x-x0) (1.5) Графики ...
... решения от численных методов расчёта. Для определения корней уравнения не требуется знания теорий групп Абеля, Галуа, Ли и пр. и применения специальной математической терминологии: колец, полей, идеалов, изоморфизмов и т.д. Для решения алгебраического уравнения n - ой степени нужно только умение решать квадратные уравнения и извлекать корни из комплексного числа. Корни могут быть определены с ...
... математики тригонометрической подстановки и проверка эффективности разработанной методики преподавания. Этапы работы: 1. Разработка факультативного курса на тему: «Применение тригонометрической подстановки для решения алгебраических задач» с учащимися классов с углубленным изучением математики. 2. Проведение разработанного факультативного курса. 3. Проведение диагностирующей контрольной ...
... «проявляется» лишь в процессе преобразований. Очевидность и «завуалированность» новой переменной мы рассмотрим на конкретных примерах во второй главе данной работы. 2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных ...


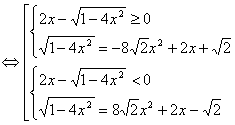
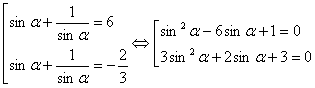
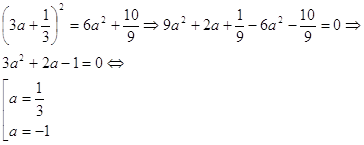
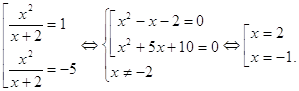
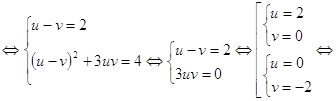
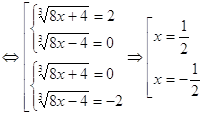
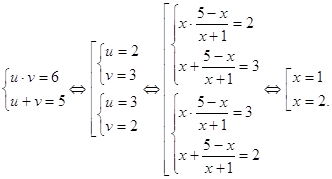
0 комментариев