Решение нелинейных уравнений. Метод деления отрезка пополам. Метод касательных. Комбинированный метод хорд и касательных
Решение систем линейных алгебраических уравнений. Методом Крамера. Методом Гаусса. Метод Жордана Гаусса. Метод Зейделя
Метод Жордана - Гаусса
Математическая обработка результатов опыта. Аппроксимация функций. Полином Лагранжа. Метод наименьших квадратов
Численные методы решения обыкновенных дифференциальных уравнений. Метод Эйлера. Метод Рунге – Кутта
Навигация
Численные методы решения обыкновенных дифференциальных уравнений. Метод Эйлера. Метод Рунге – Кутта
Методы решения алгебраических уравнений
35539
знаков
6
таблиц
3
изображения
4. Численные методы решения обыкновенных дифференциальных уравнений. Метод Эйлера. Метод Рунге – Кутта
1. Метод Эйлера. Дифференциальное уравнение y’=f(x, y) определяет на плоскости так называемое поле направлений, т.е. в каждой точке плоскости, в которой существует функция f(x, y) задает направление интегральной кривой уравнения, проходящей через эту точку. Пусть требуется решить задачу Коши, т.е. найти решение уравнения y’=f(x, y), удовлетворяющее начальному условию y(x0)=y0. Разделим отрезок [x0, X] на n равных частей и положим (X-x0)/n=h (h – шаг изменения аргумента).Допустим, что внутри элементарного промежутка от x0 до x0+h функция y’ сохраняет постоянное значения f(x0,y0,). Тогда 
где y1 – значения искомой функции, соответствующее значению х1=x0+h. Отсюда получаем 
Повторяя эту операцию, получим последовательные значения функции:
Таким образом, можно приближенно построить интегральную кривую в виде ломаной с вершинами Mr (xr; yr), где 
Этот метод называется методом ломаных Эйлера, или просто методом Эйлера.
2. Метод Рунге – Кутта. Пусть функция у определяется дифференциальным уравнением y’=f(x, y) при начальном условии y(x0)=y0. При численном интегрировании такого уравнения методом Рунге – Кутта определяют четыре числа:
Если положить 
то можно доказать что 
Схема вычислений имеет вид
|
|
|
| Добавка |
|
|
|
|
|
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
5. Практический раздел
1.Решение не линейных уравнений.
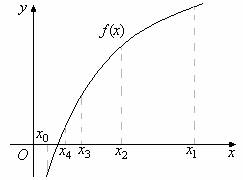
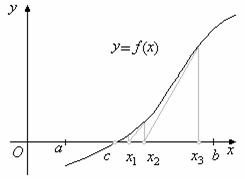
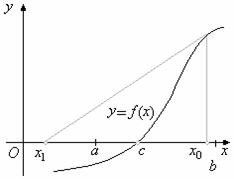
1. Отделить корни графический и уточнить один из них методом касательных с точностью 
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Singf(x) | - | - | - | - | - | - | - | + |
т.к. 
то 
x1=6,488
x2=6,401
x3=6,39756
x4=6,397567
2. Решение систем линейных алгебраических уравнений.
1. Решить систему методом Жордана – Гаусса
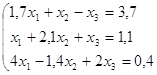
Похожие работы
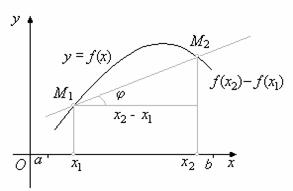
... - в методе Ньютона наблюдается ускорение сходимости процесса приближений. 5. Метод касательных (метод Ньютона) Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f ¢(x) (x-x0) (1.5) Графики ...
... решения от численных методов расчёта. Для определения корней уравнения не требуется знания теорий групп Абеля, Галуа, Ли и пр. и применения специальной математической терминологии: колец, полей, идеалов, изоморфизмов и т.д. Для решения алгебраического уравнения n - ой степени нужно только умение решать квадратные уравнения и извлекать корни из комплексного числа. Корни могут быть определены с ...
... математики тригонометрической подстановки и проверка эффективности разработанной методики преподавания. Этапы работы: 1. Разработка факультативного курса на тему: «Применение тригонометрической подстановки для решения алгебраических задач» с учащимися классов с углубленным изучением математики. 2. Проведение разработанного факультативного курса. 3. Проведение диагностирующей контрольной ...
... «проявляется» лишь в процессе преобразований. Очевидность и «завуалированность» новой переменной мы рассмотрим на конкретных примерах во второй главе данной работы. 2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных ...
0 комментариев