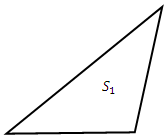
Дано: треугольник с вершинами в точках А [4; 0] B [3; 20] и C [5; 0].
Найти:
a) Уравнение прямой АВ;
b) Уравнение высоты СD, проведенной к стороне АВ;
c) Уравнение прямой СЕ, параллельной стороне АВ;
d) Площадь треугольника АВС
Решение:
А) Уравнение прямой АВ найдем по формуле:
![]() , где
, где
X1, Y1 – координаты первой точки,
X2, Y2 – координаты второй точки.
![]()
![]()
![]()
В) Уравнение высоты СD найдем, используя следующий алгоритм:
1. Найдем угловой коэффициент[1], используя условие перпендикулярности прямых[2]:
![]() , где
, где
K1 – угловой коэффициент прямой АВ
K2 – угловой коэффициент прямой СD
![]()
2. Найдем уравнение прямой с угловым коэффициентом k2, проходящая через точку С [5; 0]:
![]() , где
, где
X1, Y1 – координаты точки,
![]()
![]()
C) Уравнение прямой СЕ найдем, используя следующий алгоритм:
1. Найдем угловой коэффициент, используя условие параллельности прямых:
![]() , где
, где
K1 – угловой коэффициент прямой АВ
K2 – угловой коэффициент прямой СЕ
![]()
2. Найдем уравнение прямой с угловым коэффициентом k2, проходящая через точку С [5; 0]:
![]() , где
, где
X1, Y1 – координаты точки,
![]()
![]()
D) Найдем площадь треугольника по формуле:
![]()
1. Найдем длину стороны АВ по формуле:
![]() , где
, где
X1, Y1 – координаты точки А,
X2, Y2 – координаты точки В,
![]()
2. Найдем длину стороны СD по формуле:
![]() , где
, где
X0, Y0 – координаты точки С,
А, B, C – коэффициенты прямой АВ (Ах+Ву+С – уравнение прямой).
Уравнение прямой АВ ![]() или
или ![]()
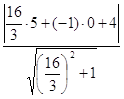
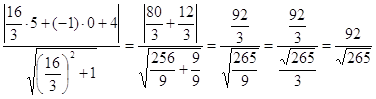
3. Найдем площадь S:
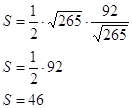
[1] Угловой коэффициент прямой — коэффициент k в уравнении y = kx + b прямой на координатной плоскости
[2] Высота треугольника (СD)— перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону (AB)
Похожие работы
... Следовательно, разность площади треугольника Рело и площади фигуры постоянного диаметра, в которую вписан правильный многоугольник, отрицательна. Из всех фигур постоянной ширины треугольник Рело имеет наименьшую площадь. 5. Применение треугольника Рело 5.1 Применение в некоторых механических устройствах Треугольник Рело находит применение во многих механических устройствах, но ни ...
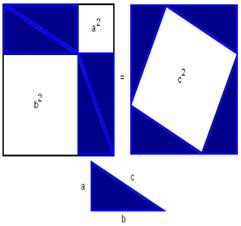
... , мы установим теперь замечательное соотношение между гипотенузой и катетами прямоугольного треугольника. Теорема, которую мы докажем, называется теоремой Пифагора. Она является важнейшей теоремой геометрии. Теорема В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Доказательство Рассмотрим прямоугольный треугольник с катетами a, b и гипотенузой c. Докажем, что . ...
... - медианы треугольников; 4. , , где BH и B1H1 высоты треугольников. §5. Опытная работа Цель опытной работы: выявление методических особенностей изучения темы «Подобные треугольники» в средней школе. Идея: для выявления методических особенностей необходимо провести несколько уроков по разработанной методики, в конце обучения провести контрольную работу, при анализе которой можно судить о ...
в треугольниках и четырехугольниках» Задачи: ü Систематизировать знания по этой теме ü Подготовиться к решению задач повышенной сложности ЕГЭ 2.Теоретическая часть 2.1 Вписанная окружность Определение: если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности. Теорема: в ...




0 комментариев