Окружности в треугольниках и четырехугольниках

Муниципальное общеобразовательное учреждение

средняя общеобразовательная школа № 8

Реферат по геометрии на тему:

Окружности в треугольниках и четырехугольниках

Работу выполнил ученик 9 «А» класса

МОУ СОШ № 8 Петров Игорь

Руководитель: учитель математики МОУ СОШ № 8

Смирнова Надежда Анатольевна

 

 

Содержание:

 

1.  Введение

2.  Теоретическая часть:

2.1 Вписанная окружность

2.2 Описанная окружность

2.3 Взаимное расположение прямой и окружности

2.4 Площади фигур

2.5 Свойства прямоугольного треугольника

3.  Практическая часть:

3.1 Задачи с окружностью, описанной около треугольника

3.2 Задачи с окружностью, вписанной в треугольник

3.3 Задачи с окружностью, описанной около четырехугольника

3.4 Задачи с окружностью, вписанной в четырехугольник

4.  Заключение

Список литературы:

1. Введение

 

Тема «Вписанные и описанные окружности в треугольниках и четырехугольниках» является одной из самых сложных в курсе геометрии. На уроках ей уделяется очень мало времени.

Геометрические задачи этой темы включаются во вторую часть экзаменационной работы ЕГЭ за курс средней школы.

Для успешного выполнения этих заданий необходимы твердые знания основных геометрических фактов и некоторый опыт в решении геометрических задач.

Цель:

ü Углубить знания по теме «Вписанная и описанная окружности в треугольниках и четырехугольниках»

Задачи:

ü Систематизировать знания по этой теме

ü Подготовиться к решению задач повышенной сложности ЕГЭ

2.Теоретическая часть

 

2.1 Вписанная окружность

 

Определение: если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.

 

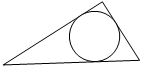
Теорема: в любой треугольник можно вписать окружность, и притом только одну.

Центр окружности, вписанной в треугольник, находится на пересечении биссектрис треугольника.

Свойство: в любом описанном четырехугольнике суммы противоположных сторон равны.

Признак: если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

 

2.2 Описанная окружность

 

Определение: если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.

Теорема: около любого треугольника можно описать окружность, и притом только одну.

Центр окружности, описанной около треугольника, находится на пересечении серединных перпендикуляров.

 

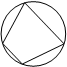
Свойство: в любом вписанном четырехугольнике сумма противоположных углов равна 180˚.

Признак: если сумма противоположных углов четырехугольника равна 180˚, то около него можно описать окружность.

2.3 Взаимное расположение прямой и окружности:

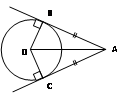
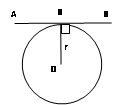
AB – касательная, если OH = r

Свойство касательной:

AB _┴ OH (OH – радиус, проведенный в точку касания H)

Свойство отрезков касательных, проведенных из одной точки:

AB = AC

ﮮ BAO = ﮮ CAO

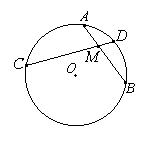
Свойство хорд: если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM ∙ MB = CM ∙ MD.

 

 

 

 

Медиана

Медиана (от лат. mediana — средняя), отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

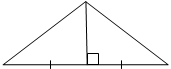
Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

Теорема: сумма углов треугольника равна 180°

Основное тригонометрическое тождество: sin² A + cos² A = 1

Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними: a² = b² + c² – 2bc ∙ cos A

 

2.4 Площади фигур

 

 

 

 

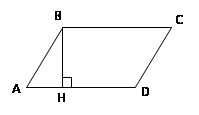
Площадь параллелограмма

Площадь параллелограмма равна произведению его основания на высоту:

·  Площадь параллелограмма равна произведению двух соседних его сторон ​на синус угла между ними:

 

Площадь треугольника

ü Площадь треугольника равна половине произведения двух его сторон на синус угла между ними:

ü Площадь треугольника равна половине произведения его основания на высоту:

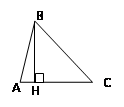
ü  Площадь прямоугольного треугольника равна половине произведения его катетов:

ü Если высоты двух треугольников равны, то их площади относятся как основания.

ü Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы:

 

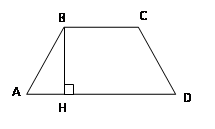
Площадь трапеции

Площадь трапеции равна произведению полусуммы её оснований на высоту:

 

Теорема: отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.