Навигация
Примеры решения задач в matlab
5. Примеры решения задач в matlab
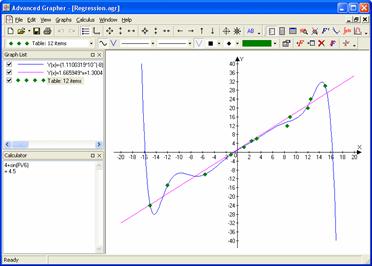
Задача 1. Построить семейство функций ![]() (
(![]() ) и найти их общие точки, при чём в объекте Figure подписать графики и точки, обозначить оси, подписать заголовок
) и найти их общие точки, при чём в объекте Figure подписать графики и точки, обозначить оси, подписать заголовок ![]() и использовать разные цвета для построенных графиков. При решении использовать функцию num2str(x), переводящее число x в строковую величину:
и использовать разные цвета для построенных графиков. При решении использовать функцию num2str(x), переводящее число x в строковую величину:
Программа:
x=-2:0.1:2;
title('{\itf(x)=x^{n}}');
xlabel('x');
ylabel('y');
hFigure=gcf;
set(hFigure,'Color',[1 1 1]);
hText=text;
set(hText,'FontSize',[18]);
for n=2:4
y=x.^n;
hold on
hPlot=plot(x,y);
set(hPlot,'Color',[1.8/n 0.7 0.5]);
set(hPlot,'LineWidth',2);
if n~=2
for i=1:length(y)
s='';
if y(i)==y1(i)
hold on
plot(x(i),y(i),'ko');
s=['(' num2str(x(i)) ',' num2str(y(i)) ')'];
hText=text(x(i),y(i)+2, s); set(hText,'FontSize',[16]);
end
end
end
y1=y; s2=['n=' num2str(n)];
hText=text(1.5, 1.5^2*n-1, s2); set(hText,'FontSize',[14]);
end
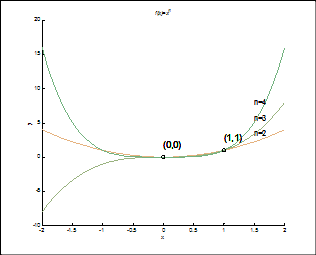
Результат (рис. 12):
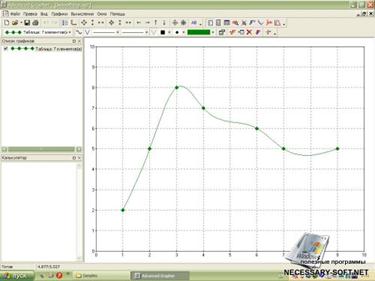
Задача 2. Написать программу-функцию, строящую график функции (funstr) и касательную к нему в точке х0.
Программа:
function kasat(funstr,x0)
f=sym(funstr); y0=subs(f,'x',x0); A=x0-1; B=x0+1; X=[A:(B-A)/100:B]; F=subs(f,'x',X);
Hline=plot(X,F); set(Hline,'LineWidth',2)
syms x
k=diff(f,x,1); K=subs(k,'x',x0); yt=sym('y0+k*(x-x0)');
yt=subs(yt,'k',K); yt=subs(yt,'x0',x0); yt=subs(yt,'y0',y0);
hold on
ezplot(yt,[A B])
plot(x0,y0,'o')
grid on
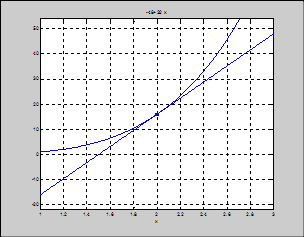
Результат (рис. 13): >> kasat('x^4',2)
Задача 3. Построить поверхность вращения графика функции заданной явно: ![]() (где
(где ![]() ), вокруг оси Ох.
), вокруг оси Ох.
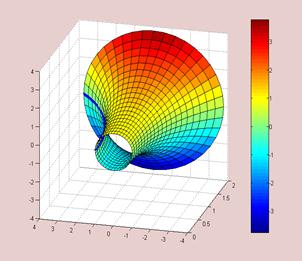
Результат (рис. 14)
Программа:
x1=0; x2=2; a=1;
u=x1:0.1:x2;
v=0:pi/20:2*pi;
[U,V]=meshgrid(u,v);
F=a*(exp(-U/a)+exp(U/a))/2;
X=U; Y=F.*cos(V); Z=F.*sin(V);
figure; hFigure=gcf;
set(hFigure,'Color',[0.9 0.8 0.8]);
surf(X,Y,Z)
colorbar;
view([-75,20])
hold on
x=0:0.1:x0; y=a*(exp(-x/a)+exp(x/a))/2;
hPlot=plot(x,y); set(hPlot,'LineWidth',5)
Задача 4. Визуализировать поверхность, образованной вращением астроиды ![]() .
.
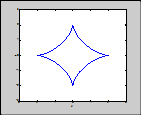
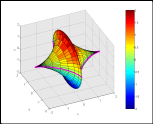
Результат (рис. 15,16)
Программа:
Построение астроиды
a=2;
t=-2*pi:pi/20:2*pi;
X=a*cos(t).^3;
Y=a*sin(t).^3;
w=300;
h=300; figure('Units','Pixels','position',
[100,100,w,h]);
plot(X,Y)
xlabel('x'); ylabel('y');
axis([-3, 3, -3, 3]);
% Поверхность вращения
a=2;
t=-2*pi:pi/20:2*pi;
X=a*cos(t).^3;
v=0:pi/20:2*pi;
[T,V]=meshgrid(t,v);
Y=a*sin(T).^3;
X1=X;
Y1=Y.*cos(V);
Z1=Y.*sin(V);
figure;
hFigure=gcf;
set(hFigure,'Color',[1 1 1]);
surf(X1,Y1,Z1)
hAxes=gca;
set(hAxes,'Color',[0.9,0.9,0.9]);
colorbar;
xlabel('x'); ylabel('y'); zlabel('z');
view([-24,40])
hold on
hPlot=plot(X,Y);
set(hPlot,'LineWidth',5)
set(hPlot,'Color',[1 0 1])
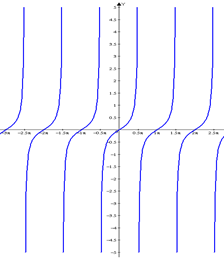
Задача 5. Построить в полярных координатах лемнискату Бернулли: ![]() .
.
Программа:
a=1;
r=[]; phi=[];
for p=0:pi/60:2*pi
if 2*a^2*cos(2*p)>=0
r=[r sqrt(2*a^2*cos(2*p))];
phi=[phi p];
end
end
hFigure=gcf;
set(hFigure,'Color',[1 1 1]);
hP=polar(phi,r);
set(hP,'LineWidth',2);
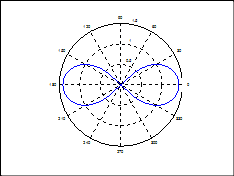
Результат (рис. 17):
Задача 6. Используя численные и символьные вычисления в MATLAB найти: а) определённый интеграл; б) двойной интеграл; в) поверхностный интеграл (1-го рода).
а) Классической задачей численного анализа является задача о вычислении определённых интегралов. Из всех методов вычисления определённых интегралов самым простым, но в то же время довольно успешно применяемым является метод трапеции. В MATLAB для этого метода предусмотрена функция: trapz(x,y) (команда edit trapz позволяет вывести текст этой функции). Одномерный массив х (вектор) содержит дискретные значения аргументов подынтегральной функции. Значения подынтегральной функции в этих точках сосредоточены в одномерном массиве y. Чаще всего для интегрирования выбирают равномерную сетку, то есть значения элементов массива х отстоят друг от друга на одну и ту же величину – шаг интегрирования. Точность вычисления интеграла зависит от величины шага интегрирования: чем меньше этот шаг, тем больше точность.
Задача 7. Вычислить интеграл 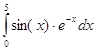 методом трапеции с различными шагами интегрирования (для наблюдения 14 десятичных цифр после запятой нужно предварительно ввести и исполнить команду format long).
методом трапеции с различными шагами интегрирования (для наблюдения 14 десятичных цифр после запятой нужно предварительно ввести и исполнить команду format long).
Программа: Результат:
function t=trap(dx)
x=0:dx:5;
y=sin(x).*exp(-x);
t=trapz(x,y); >> format long
>> trap(1)
ans = 0.42255394026468
>> trap(0.1)
ans = 0.50144886299125
>> trap(0.01)
ans = 0.50226667654901
>> trap(0.001)
ans = 0.50227485744814
Метод трапеций является очень универсальным методом и хорошо подходит интегрирования не слишком гладких функций. Если же функция под знаком интеграла является гладкой (существуют и непрерывны несколько первых производных), то лучше применять методы интегрирования более высоких порядков точности. При одном и том же шаге интегрирования методы более высоких порядков точности достигают более точных результатов.
В системе МАТLАВ методы интегрирования более высоких порядков точноcти реализуются функциями quad (метод Симпсона) и quad8 (метод Ньютона-Котеса 8-го порядка точности). Оба этих метода являются к тому же адаптивными. Последнее означает, что пользователю нет необходимости контролировать достигнутую точность результата путем сравнения последовательных значении, соответствующих разным шагам интегрирования. Все это указанные данные функции выполняют самостоятельно.
У функции quad8 более высокий порядок точности по сравнению с функцией quad, что очень хорошо для гладких функций, так как обеспечивается более высокая точность результата при большем шаге интегрирования (меньшем объеме отчислений). Однако функция quad может иметь не меньшее, а даже большее быстродействие для не слишком гладких функций (разрывны или велики по абсолютной величине вторая или третья производные). В любом случае обе эти функции по умолчанию обеспечивают одинаковую относительную точность результата, равную 0.001.
Как и многие другие функции системы МАТLАВ, функции quad и quad8 могут принимать различное количество параметров. Минимальный формат вызова этих функций включает в себя три параметра: имя подынтегральной функции, нижний предел интегрирования и верхний предел интегрирования. Если применяется четвертый параметр, то он является требуемой относительной точностью результата вычислений. Кстати, если обе эти адаптивные функции не могут обеспечить получение необходимой точности (расходящийся или близкий к этому интеграл), то они возвращают символическую бесконечность Inf.
Для вычисления определённых интегралов символьными методами можно использовать два варианта решения: напрямую или по этапам (с подстановкой символьных чисел).
Задача 8. Вычислить определённый интеграл ![]() .
.
Программа: Результат:
a1=sym('0'); b1=sym('2');
syms w t a b
w=t^2;
% 1 способ: работа с подстановкой символьных чисел
symbol=int(w,'t',a,b)
symbol2a=subs(symbol,[a,b],[a1,b1])
digits(20);
number=vpa(symbol2a)
% 2 способ: работа с символьными числами
symbol2b=int(w,'t',a1,b1) symbol =
1/3*b^3-1/3*a^3
symbol2a =
8/3
number =
2.6666666666666666667
symbol2b =
8/3
Задача 9. Вычислить площадь поверхности, полученной вращением астроиды вокруг оси Ox: ![]() . (поверхность визуализирована в задаче 2).
. (поверхность визуализирована в задаче 2).
Программа: Результат:
t1=sym('0'); t2=sym('pi/2'); a=sym('1');
syms x y t f
x=a*cos(t)^3; y=a*sin(t)^3;
f=y.*sqrt(diff(x)^2+diff(y)^2);
symbol=simplify(int(4*pi*f,'t',t1,t2))
digits(10);
number=vpa(symbol) symbol =
12/5*pi
number =
7.539822370
б) Двойные интегралы сводятся к вычислению повторных определённых интегралов, один из которых является внутренним, а другой внешним. Внутренний интеграл является подынтегральной функцией для внешнего интеграла. Можно было бы для численных вычислений написать некоторую цепочку вычислений, в которой многократные вычисления подынтегральной функции сводились бы к многократным вызовам функции quad. Однако нет необходимости делать это самостоятельно, так как в системе MATLAB для этого имеется специальная функция dblquad.
Задача 8. Вычислить интеграл 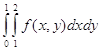 , где
, где ![]() .
.
Программа:
Результат:
function z=fof(x,y)
z=x.*sin(y)+y.*sin(x); >> format long
>> dblquad('fof',0,1,1,2)
ans =
1.16777110966887
Задача 9. С помощью символьных вычислений получить следующие интегралы ![]() ,
, 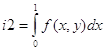 ,
, ![]() ,
, 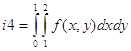 ,
, 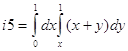 , где
, где ![]() .
.
Программа:
syms x y
z=sym('x*sin(y)+y*sin(x)');
i1=int(z,'x')
i2=int(z,'x',0,1)
i3=int(int(z,'x'),'y')
i4=int(int(z,'x',1,2),'y',0,1)
digits(14);
number4=vpa(i4)
i5=int(int(x+y,'y',x,1),'x',0,1) i1 =
1/2*x^2*sin(y)-y*cos(x)
i2 =
1/2*sin(y)-y*cos(1)+y
i3 =
-1/2*x^2*cos(y)-1/2*y^2*cos(x)
i4 =
-1/2*cos(2)-cos(1)+3/2
number4 =
1.1677711124054
i5 =
1/2
Так как символьные вычисления не дают погрешности метода вычисления и сами по себе они более точные, то можно увидеть, что функция dblquad даёт точный результат до 7 знака после запятой.
в) Из высшей математики известно, что к определенным и двойным интегралам могут быть сведены многие другие типы интегралов, например поверхностный интеграл 1-го рода. Так как при его нахождении используется дифференцирование под знаком интеграла, то использовать численные вычисления некорректно.
Задача 10. Вычислить поверхностный интеграл 1-го рода: ![]() , где S – часть плоскости
, где S – часть плоскости ![]() , лежащая в первом октанте (по теореме 2).
, лежащая в первом октанте (по теореме 2).
Программа: Результат:
syms x y z f1 f2
f1=1-x-y;
f2=x*y*z;
fun=subs(f2,z,f1)
d=1+diff(f1,x)^2+diff(f1,y)^2
syms x1 x2 y1 y2
x1=sym('0');
x2=sym('1');
y1=sym('0');
y2=sym('1-x');
intpov1=int(int(fun*sqrt(d),'y',y1,y2),'x',x1,x2)
digits(10);
number=vpa(intpov1) fun =
x*y*(1-x-y)
d =
3
intpov1=
1/120*3^(1/2)
number =
1443375673e-1
Задача 11. Вычислить поверхностный интеграл 1-го рода ![]() , где S - сфера
, где S - сфера ![]() (по теореме 3).
(по теореме 3).
Сначала создадим функцию, описывающую поверхность по которой происходит интегрирование:
function [x,y,z]=pov;
syms x y z u v a
x=a*sin(u)*cos(v);
y=a*sin(u)*sin(v);
z=a*cos(u);
Программа:
syms x y z u v a
f=sym('x^2+y^2');
[x0,y0,z0]=pov;
syms E G F W
E=diff(x0,'u')^2+diff(y0,'u')^2+diff(z0,'u')^2;
G=diff(x0,'v')^2+diff(y0,'v')^2+diff(z0,'v')^2;
F=diff(x0,'u')*diff(x0,'v')+diff(y0,'u')*
diff(y0,'v')+diff(z0,'u')*diff(z0,'v');
W=sqrt(E*G-F^2); f2=W*subs(f,[x,y],[x0,y0]);
syms u1 u2 v1 v2
u1=sym('0');
u2=sym('pi/2');
v1=sym('0');
v2=sym('pi/2');
p=sym('8');
intpov=p*int(int(f2,'v',v1,v2),'u',u1,u2)
intpov2=simplify(intpov)
digits(10);
number=vpa(intpov2)
b=sym('1');
int=subs(intpov2,a,b) intpov =
4/3*a^2*pi*(a^4)^(1/2)*4^(1/2)
intpov2 =
8/3*a^4*pi*csgn(a^2)
number =
8.377580412*a^4*csgn(a^2)
int =
8/3*pi
Примечание. Функция сsgn является специфической в MATLAB. Она не может быть введена пользователем и возникает только при оперировании с функцией simplify (упрощение символьных выражений). Например:
>> syms a t
>> t=csgn(a^2)*a^2
??? Undefined function or variable 'csgn'.
>> simplify((a^4)^(1/2))
ans =
csgn(a^2)*a^2
>> simplify((a^8)^(1/4))
ans =
(a^8)^(1/4)
>> simplify((a^9)^(1/3))
ans =
(a^9)^(1/3)
Список использованных источников1. Ануфриев, И.Е. Самоучитель MatLab 5.3/6.х / И.Е. Ануфриев. - СПб.: БХВ-Петербург, 2002. - 736 с.
2. Берман, Г.Н. Сборник задач по курсу математического анализа / Г.Н. Берман, И.Г. Араманович, А.Ф. Бермант и др. - М.: Наука, 1966. - 456 с.
3. Бермант, А.Ф. Краткий курс математического анализа для втузов / А.Ф. Бермант, И.Г. Араманович. - М.: Наука, 1966. - 736 с.
4. Гультяев, А. Визуальное моделирование в среде MatLab / А. Гультяев. - СПб.: Питер, 2001. - 553 с.
5. Демидович, Б.П. Задачи и упражнения по математическому анализу для втузов / Б.П. Демидович, Г.С. Бараненков, В.А. Ефименко и др. - М.: Наука, 1966. - 472 с.
6. Лазарев, Ю.Ф. MatLab 5.х / Ю.Ф. Лазарев. - Киев: BHV, 2000. - 388 с.
7. Мартынов, Н.Н. Matlab 5.х: вычисления, визуализация, программирование / Н.Н. Мартынов, А.П. Иванов. - М.: КУДИЦ-ОБРАЗ, 2000. - 336 с.
8. Куринной, Г.Ч. Математика: Справочник / Г.Ч. Куринной. - Харьков: Фолио; Ростов на Дону: Феникс, 1997. - 463 с.
9. Пискунов, Н.С. Дифференциальное и интегральное исчисление для втузов в 2 томах / Н.С. Пискунов. - М.: Наука, 1966. - 2 т. - 312 с.
10. Фихтенгольц, Г.М. Курс дифференциального и интегрального исчисления в 3 томах / Г.М. Фихтенгольц. - М.: Государственное изд-во физико-математической литературы, 1959. - т. 1-3.
11. Сайты http://www/informika.ru, htt://www.softline.ru, http://matlab.ru.
Похожие работы
... (5.16) Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f(x). В вычислительной практике используются другие оценки. Вычтем из равенства (5.15) равенство (5.16): Ih/2 – Ih » Chk(2k – 1). (5.17) Учитывая приближенное равенство (5.16), получим следующее приближенное ...
... , которая состоялась 22 февраля 1995 года, обсуждался ход реализации программы информатизации образования на 1994-1995 гг. Был рассмотрен вопрос о совершенствовании организации обучения информатике в общеобразовательной школе на современном этапе. Коллегия постановила признать целесообразной необходимость выделения нескольких этапов в овладении основами информатики и формировании информационной ...
... разработчиками. На сегодняшний день существует широкий спектр программ от простейших, контролирующих до сложных мультимедийных продуктов. 2. Опытно-экспериментальная работа по формированию познавательной потребности у учащихся средствами информационных технологий 2.1 Особенности изучения темы "Интеграл" в школьном курсе математики Выбор темы "Интеграл" неслучаен. Тема "Интеграл" изучается ...


0 комментариев