Навигация
Практическое применение теории нечетких множеств
3. Практическое применение теории нечетких множеств
Под конкурентоспособностью понимают комплекс потребительских, стоимостных и социальных характеристик товара (изделия), определяющих его успех на данном рынке, т. е. способность данного товара быть обмененным на деньги на конкретном рынке в условиях широкого предложения к обмену других товаров-аналогов. Конкурентоспособность — это степень соответствия совокупности свойств объекта ценностной системе рынка. Границы понятия конкурентоспособность непрерывно расширяются, переходя от конкурентоспособности изделия к конкурентоспособности предприятий и даже государств. Конкурентоспособность обеспечивается высоким технологическим уровнем и качеством, соответствием требованиям и стандартам стран-импортеров, фирм-покупателей, высоким уровнем технологического обслуживания, патентной чистотой и патентной защитой, приемлемой ценой, льготными условиями платежа и т. д. Фирме, занимающейся реализацией компьютеров, необходимо из шести предложенных марок ноутбуков ASUS L8400, ASUS T9, FUJITSU – SIEMENS LIFEBOOK B, IRU NOVIA 1012DVD, COMPAQ EVO N610C, INTEL JS2310 выбрать модель с оптимальным набором характеристик (дисплей с большим количеством точек, процессор с высокой тактовой частотой, большой объем оперативной памяти, жесткий диск с большим объемом памяти, долгий срок автономной работы, маленький вес, низкая стоимость, большой гарантийный срок ). Известно, что ноутбук ASUS L8400 обладает следующими качествами: дисплей 14.5 точек, процессор 1 ГГц, память 256 Мбайт, жесткий диск 20 Гбайт, привод DVD-ROM, время автономной работы 2,7 часа, вес 2.9 кг, цена 1.5 тыс. долларов США, гарантийный срок 3 года. Ноутбук ASUS T9 обладает следующими качествами: дисплей 14.1 точек, процессор 0.8 ГГц, память 128 Мбайт, жесткий диск 15 Гбайт, привод DVD-ROM, время автономной работы 2.5 часа, вес 2.1кг, цена 1.16 тыс. долларов США, гарантийный срок 2 года. Ноутбук FUJITSU–SIEMENS LIFEBOOK B: дисплей 10.4 точек, процессор 0.7 ГГц, память 256 Мбайт, жесткий диск 30 Гбайт, привод CD-RW, время автономной работы 2.4 часа, вес 1.6кг, цена 2 тыс. долларов США, гарантийный срок 2.5 года. Ноутбук IRU NOVIA 1012DVD: дисплей 12.0 точек, процессор 1.06 ГГц, память 128 Мбайт, жесткий диск 20 Гбайт, привод DVD-CDRW, время автономной работы 2.5 часа, вес 1.7 кг, цена 1.48 тыс. долларов США, гарантийный срок 1 год. Ноутбук COMPAQ EVO N610C: дисплей 14.0 точек, процессор 1.6 ГГц, память 256 Мбайт, жесткий диск 40 Гбайт, привод DVD-CDRW, время автономной работы 2.4 часа, вес 2.1 кг, цена 2 тыс. долларов США, гарантийный срок 3 года. Ноутбук INTEL JS2310: дисплей 14.0 точек, процессор 1.12 ГГц, память 256 Мбайт, жесткий диск 25 Гбайт, привод CD-RW, время автономной работы 2.5 часа, вес 1.9 кг, цена 1.37 тыс. долларов США, гарантийный срок 1 год. Данная задача может быть решена с помощью метода нечеткого отношения предпочтения /3/. Задачу выбора определенной марки ноутбука с учетом наиболее важных критериев качества рассмотрим на примере анализа альтернатив: a1 – ASUS L8400, a2 – ASUS T9, a3 – FUJITSU–SIEMENS LIFEBOOK B, a4 – IRU NOVIA 1012DVD, a5 - COMPAQ EVO N610C, a6 – INTEL JS2310. Для оценки альтернатив используем девять критериев качества, где, на основе данных об основных характеристиках ноутбуков задаются множества значений, которые могут принимать различные характеристики: F1- дисплей (от 10 до 15 тыс. точек.), интерес представляет дисплей с большим количеством точек; F2- процессор (от 0,6 до 1,7 ГГц), предпочтение отдается процессору с большей тактовой частотой; F3- память (от 120 до 300 Мбайт), интерес представляет ноутбук с большим объемом памяти; F4- жесткий диск (от 10 до 45 Гбайт), предпочтение отдается жесткому диску с большим объемом памяти; F5- привод (от 1 до 10 баллов), предпочтение составляет большее количество баллов; F6- время автономной работы (от 2 до 3,5 часов), предпочтительнее большее количество часов автономной работы; F7- вес (от 1 до 3 кг), интерес составляет ноутбук с меньшим весом; F8- стоимость (от 1 до 3 тыс. долларов США), предпочтение отдается ноутбуку с меньшей ценой;
F9- срок гарантии (от 0,5 до 3,5 лет), предпочтение отдается ноутбуку с большим гарантийным сроком.
Теперь на основании функций принадлежности всех альтернатив находятся их значения по девяти критериям /6/. Для функции принадлежности утверждения «величина х мала» m(C) рассчитывается по формуле:
![]()
1, 0 < х < а1
m(C)= ![]() , а1≤ х ≤ а2 (12)
, а1≤ х ≤ а2 (12)
0, х> а2
Для функции принадлежности утверждения «величина х большая» m(C) рассчитывается по формуле:
![]() 0, 0 < х < а1
0, 0 < х < а1
m(C)= ![]() , а1≤ х ≤а2 (13)
, а1≤ х ≤а2 (13)
1, х > а2
Для F1 значение m(F1) рассчитывается по следующей формуле
![]() 0, 0 < х < 10
0, 0 < х < 10
m(F1)= ![]() , 10 ≤х ≤ 15
, 10 ≤х ≤ 15
1, х > 15
μF1={0.9/ а1; 0.8/ а2; 0.1/ а3; 0.4/ а4; 0.7/ а5; 0.7/ а6}
|
|
|
|
|
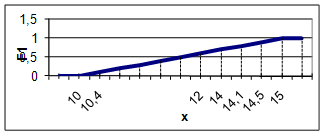
Рисунок 5– График функции принадлежности для F1
Для F2 значение m(F2) рассчитывается по следующей формуле
![]() 0, 0< х < 0,7
0, 0< х < 0,7
m(F2)= ![]() , 0,6 ≤ х ≤ 1,7
, 0,6 ≤ х ≤ 1,7
1, х > 1,7
μF2={0.6/ а1; 0.4/ а2; 0.3/ а3; 0.7/ а4; 0.9/ а5; 0.8/ а6}
|
|
|
|
|
|
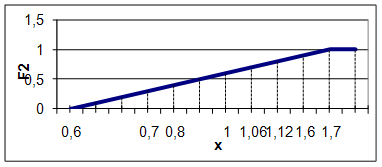
Рисунок 6 - График функции принадлежности для F2
Для F2 значение m(F3) рассчитывается по следующей формуле
![]() 0, 0 < х < 120
0, 0 < х < 120
m(F3)= ![]() , 120 ≤ х ≤ 300
, 120 ≤ х ≤ 300
1, х > 300
μF3={0.8/ а1; 0.4/ а2; 0.8/ а3; 0.4/ а4; 0.8/ а5; 0.8/ а6}
|
|
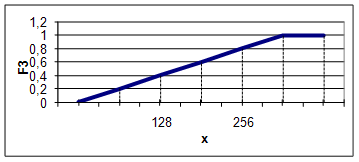
Рисунок 7 - График функции принадлежности для F3
Для F4 значение m(F4) рассчитывается по следующей формуле
![]() 0, 0 < х < 10
0, 0 < х < 10
m(F4)= ![]() , 10 ≤ х ≤ 45
, 10 ≤ х ≤ 45
1, х > 45
μF4={0.3/ а1; 0.1/ а2; 0.6/ а3; 0.3/ а4; 0.9/ а5; 0.4/ а6}
|
|
|
|
|
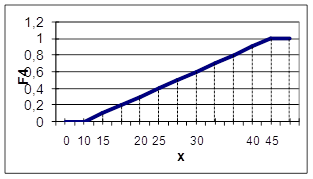
Рисунок 8 - График функции принадлежности для F4
Для F5 значение m(F5) рассчитывается по следующей формуле
![]()
0, 0 < х < 1
m(F5)= ![]() , 1 ≤ х ≤ 10
, 1 ≤ х ≤ 10
1, х > 10
μF5={0.5/ а1; 0.6/ а2; 0.3/ а3; 0.8/ а4; 0.8/ а5; 0.3/ а6}
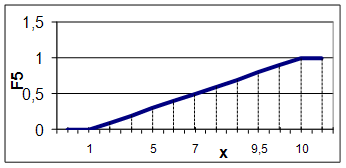
|
Для F6 значение m(F6) рассчитывается по следующей формуле
![]() 0, 0 < х < 2
0, 0 < х < 2
m(F6)= ![]() , 2 ≤ х ≤ 3.5
, 2 ≤ х ≤ 3.5
1, х > 3.5
μF6={0.7/ а1; 0.3/ а2; 0.2/ а3; 0.3/ а4; 0.2/ а5; 0.3/ а6}
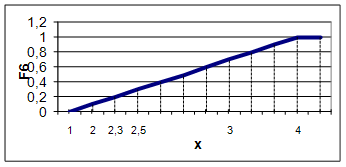
Рисунок 10 - График функции принадлежности для F6
Для F7 значение m(F7) рассчитывается по следующей формуле
![]() 1, 0 < х < 1
1, 0 < х < 1
m( F7)= ![]() , 1 ≤ х ≤3
, 1 ≤ х ≤3
0, х > 3
μF7={0.3/ а1; 0.5/ а2; 0.7/ а3; 0.8/ а4; 0.5/ а5;0.6/ а6}
|
|
|
|
|
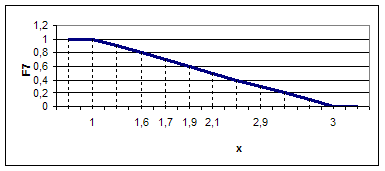
Рисунок 11 - График функции принадлежности для F7
Для F8 значение m(F8) рассчитывается по следующей формуле
![]() 1, 0 < х < 1
1, 0 < х < 1
m( F8)= ![]() , 1 ≤ х ≤ 3
, 1 ≤ х ≤ 3
0, х > 3
μF8={0.6/ а1; 0.9/ а2; 0.5/ а3; 0.8/ а4; 0.5/ а5; 0.7/ а6}
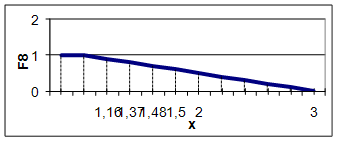
Рисунок 12 - График функции принадлежности для F8
Для F9 значение m(F9) рассчитывается по следующей формуле
![]() 0, 0 < х < 0.5
0, 0 < х < 0.5
m(F9)= ![]() , 0.5 ≤ х ≤3,5
, 0.5 ≤ х ≤3,5
1, х > 3,5
μF9={0.9/ а1; 0.6/ а2; 0.8/ а3; 0.4/ а4; 0.9/ а5; 0.4/ а6}
|
|
|
|
|
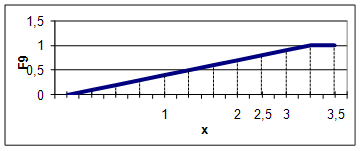
Рисунок 13 - График функции принадлежности для F9
На основе графиков функций принадлежности всех альтернатив по девяти критериям определены их конкретные значения.
По этим данным составим матрицы нечётких отношений предпочтения R1 ,…,R9, причём элементы этих матриц находятся по формуле (14):
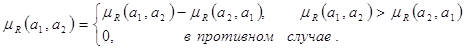 (14)
(14)
mR1 =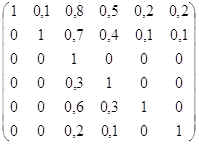 mR2 =
mR2 =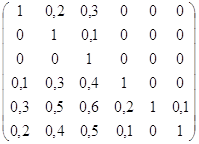
mR3 =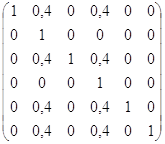 mR4 =
mR4 =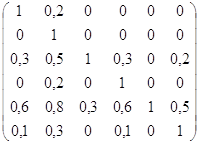
mR5 =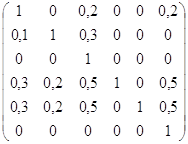 mR6 =
mR6 =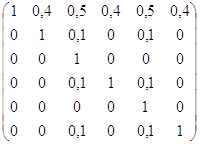
mR7 =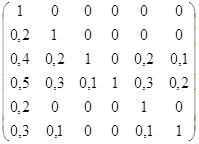 mR8 =
mR8 =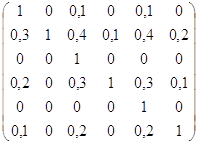
mR9 =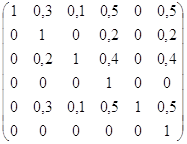
Задача выбора решается в соответствии с описанной выше процедурой, строится нечеткое отношение Q1 = R1 Ç R2 Ç …Ç R9:
Q1=
Находится множество недоминируемых альтернатив на множестве {A, μQ1}: получаем множество ![]() НД=║1,1,1,1,1,1║
НД=║1,1,1,1,1,1║
Строится отношение Q2:
Коэффициенты wk относительной важности критериев по оценке автора работы имеют следующие значения:
W1=0,1; W2=0,15; W3=0,1; W4=0,15; W5=0,09; W6=0,1; W7=0,05; W8=0,2; W9=0,06.
Определяется нечёткое отношение Q2:
![]() (15)
(15)
mQ2(a1,a2)= 0,1*0,1 + 0,15*0,2 + 0,1*0,4 + 0,15*0,2 + 0,09*0 + 0,1*0,2 + +0,05*0 + 0,2*0 + 0,06*0,2 = 0,142.
Аналогично вычисляем остальные элементы матрицы.
Q2=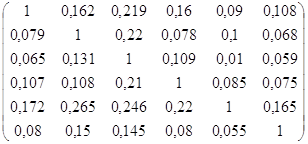
Находится подмножество недоминируемых альтернатив множества {А, ![]() }:
}:
![]() (16)
(16)
по всем i и j (i¹j),Находится подмножество недоминируемых альтернатив множества {A, μQ2}:
μQ2н,д,(а1)=1- max{0; 0,162 – 0,079; 0,219 – 0,065;0,16 – 0,107; 0,09 – 0,172; 0,108 – 0,08}= 0,846
μQ2н,д,(а2)=1- max{0,079 – 0,162; 0; 0,22 – 0,131; 0,078 – 0,108; 0,1 – 0,265; 0,068 – 0,15}= 0,911,
μQ2н,д,(а3)=1- max{0,065 - 0,219; 0,131 – 0,22;0; 0,104 – 0,21; 0,01 – 0,246; 0,059 – 0,145}= 1
μQ2н,д,(а4)=1- max{0,107 - 0,16; 0,108 – 0,078; 0,21 – 0,109;0;0,085 – 0,22; 0,075 – 0,08}= 0,899
μQ2н,д,(а5)=1- max{0,172 – 0,09; 0,265 – 0,1; 0,246 – 0,01; 0,22 – 0,085; 0 ; 0,165 – 0,055}= 0,764
μQ2н,д,(а6)=1- max{0,08 – 0,108; 0,15 – 0,068; 0,145 – 0,059; 0,08 – 0,075; 0,055 - – 0,165; 0 }= 0,914
В результате получается: μQ2н,д,(ai)=(0,846 0,911 1 0,899 0,764 0,914)
Результирующее множество недоминируемых альтернатив есть пересечение множеств μQ1н,д, и μQ2н,д,:
μQ1н,д, Ç μQ2н,д,={(1 1 1 1 1 1) Ç (0,846 0,911 1 0,899 0,764 0,914)}= =(0,846 0,911 1 0,899 0,764 0,914)
Следовательно, рациональным следует считать выбор альтернативы a3, имеющей максимальную степень недоминируемости, равную 1.
Таким образом, с учетом всех перечисленных критериев и их относительной важности, наилучшим для фирмы, занимающейся реализацией компьютеров, будет выбор ноутбука модели FUJITSU–SIEMENS LIFEBOOK B.
Заключение
В данной курсовой работе были рассмотрены такие разделы дискретной математики как применение математической логики, теории графов и элементов теории нечётких множеств. Было рассмотрено на конкретных примерах, как алгоритмы дискретной математики применяются в сфере экономики, в частности, при решении проблемы выбора из нескольких альтернатив.
В первой части курсовой работы было рассмотрено применение методов дискретной математики и математического моделирования в экономике и математической логике, где рассматриваются логические операции и преобразование логических функций, приведение функций к дизъюнктивной и конъюнктивной нормальной форме, построение таблицы истинности, нахождение полинома Жегалкина для заданной функции и её производных по одной и двум переменным.
Во второй части на конкретных примерах рассматривается практическое применение теории графов в экономике. Были решены экономические задачи с использованием таких алгоритмов, как «жадный» (алгоритм Краскала) и алгоритма Дейкстры. Составлены математические модели данных алгоритмов. С помощью венгерского метода, было получено решение для задачи коммивояжера.
В третьей части решена задача, целью которой является выбор оптимальной альтернативы, из шести предложенных. Решение было получено посредством многокритериального выбора альтернатив на основе нечёткого отношения предпочтения. Данный способ весьма удобен для решения различных экономических задач. Для расчетов, в третьей части, использовался табличный редактор «Excel», в целях экономии времени, затрачиваемого на вычисления, а также для наибольшей точности расчетов.
Список использованных источников
1. Яблонский С.В. Введение в дискретную математику: Учеб. пособие / Под ред. В.А. Садовничего. – 3-е изд.; стер. – М.: Высшая школа, 2001. – 384 с.
2. Новиков Ф.А. Дискретная математика для программистов. СПб., Питер, 2002. 304 с.
3. Матюхина Л.Я. Математическое моделирование в экономике: методические указания к курсовой работе. Хабаровск, 2002. 20 с.
4. Белоусов А.И, Ткачев С.Б. Дискретная математика. М., Издательство МГТУ имени Н.Э. Баумана, 2003, 631 с.
5. Гаврилов С.П. Сапоженко А.А. Сборник задач по дискретной математике. – М.: Наука, 1978
6. Галкина В.А. Дискретная математика: комбинаторные методы оптимизации. М., Наука, 2003, 232с.
7. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики. М., Высшая школа, 2004, 128 с.
8. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1988.
9. Свами М.Н., Тхуласираман К. Графы, сети и алгоритмы: Пер. с англ. – М.: Мир, 1984. – 455 с.
Похожие работы
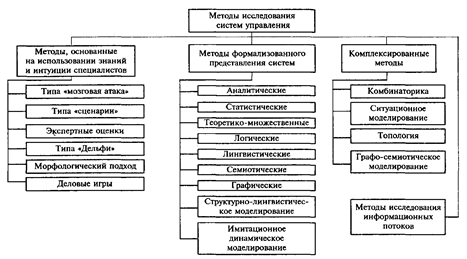
... и др. Они сформировались путем интеграции экспертных и формализованных методов. Схема классификации методов приведена на рис. 1 Рис. 1 - Классификация методов исследования систем управления 2. МЕТОДЫ ФОРМАЛИЗОВАННОГО ПРЕДСТАВЛЕНИЯ СИСТЕМ В ИССЛЕДОВАНИЯХ В настоящее время известны различные классификации методов формализованного представления систем. В результате этого методы, иногда ...
... . Вторая группа - методы формализованного представления систем управления, основанные на использовании математических, экономико-математических методов и моделей исследования систем управления. Среди них можно выделить следующие классы: аналитические (включают методы классической математики - интегральное исчисление, дифференциальное исчисление, методы поиска экстремумов функций, вариационное ...
... на одном этапе исследования, а иные – на другом. ЗАКЛЮЧЕНИЕ В процессе написания курсовой работы мною была изучена такая тема: «Аудит как метод исследования». Выяснила, что аудит входит в комплексно-комбинированные методы исследования систем управления, это указано на рис. 1, см. приложение 1. Комплексно-комбинированные методы исследования систем управления базируются на использовании ...
... . Это обстоятельство учитывается не только на этапе построения модели, но и на завершающей стадии, когда происходит объединение и обобщение результатов исследования, получаемых на основе многообразных средств познания. Моделирование - циклический процесс. Это означает, что за первым четырехэтапным циклом может последовать второй, третий и т.д. При этом знания об исследуемом объекте расширяются и ...

0 комментариев