Навигация
Міністерство освіти і науки України
Дніпропетровський національний університет ім. Олеся Гончара
КОНТРОЛЬНА РОБОТА
з дисципліни „Диференціальні рівняння"
на тему „Особливі точки”
Виконавець: студентка групи
Назаренко Олеся
Перевірив:
м. Дніпропетровськ 2010 р.
Зміст
1. Особливі точки
2. Задача 1
3. Задача 2
4. Задача 3.
5. Задача 4
1. Особливі точки
Особливою точкою системи
![]() (1)
(1)
або рівняння
![]() (2)
(2)
де функції ![]() й
й ![]() неперервно диференційовані, називається така точка, в якій
неперервно диференційовані, називається така точка, в якій ![]() .
.
Для дослідження особливої точки системи
![]() (3)
(3)
або рівняння
![]() (4)
(4)
треба знайти розв’язок характеристичного рівняння
![]() (5)
(5)
Якщо розв’язки ![]() дійсні, різні
дійсні, різні ![]() й одного знаку
й одного знаку ![]() , то особлива точка - вузол (рис.1, а), причому стійкий, якщо
, то особлива точка - вузол (рис.1, а), причому стійкий, якщо ![]() й нестійкий, якщо
й нестійкий, якщо ![]() .
.
Вузол характеризується тим, що всі траєкторії, крім однієї II, мають у точці (0,0) загальну дотичну I, що сама є траєкторією. Прямі I і II спрямовані вздовж власних векторів матриці ![]() , які відповідають
, які відповідають ![]() і
і ![]() , причому пряма I відповідає меншому за модулем з
, причому пряма I відповідає меншому за модулем з ![]() і
і ![]() .
.
При ![]() вузол є стійкою точкою спокою. На рис.1а стрілками показаний напрямок руху вздовж траєкторії при зростанні
вузол є стійкою точкою спокою. На рис.1а стрілками показаний напрямок руху вздовж траєкторії при зростанні ![]() у випадку стійкого вузла. Якщо
у випадку стійкого вузла. Якщо ![]() , то вузол нестійкий і стрілки заміняються на протилежні.
, то вузол нестійкий і стрілки заміняються на протилежні.
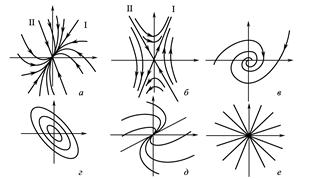
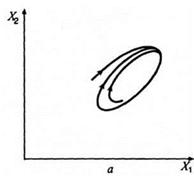
Рис.1. Типові траєкторії [2]
Якщо розв’язки ![]() дійсні, різні
дійсні, різні ![]() й різних знаків
й різних знаків ![]() , то особлива точка - сідло (рис.1, б). Сідло є нестійкою точкою спокою.
, то особлива точка - сідло (рис.1, б). Сідло є нестійкою точкою спокою.
Сідло характеризується наявністю двох траєкторій I і II, що проходять через (0,0) також у напрямку власних векторів. Пряма I є асимптотою для інших траєкторій при ![]() , а II є асимптотою при
, а II є асимптотою при ![]() . Прямолінійна траєкторія I розташована за напрямком власного вектора, що відповідає додатньому
. Прямолінійна траєкторія I розташована за напрямком власного вектора, що відповідає додатньому ![]() , а прямолінійна траєкторія II за напрямком власного вектора, що відповідає від‘ємному
, а прямолінійна траєкторія II за напрямком власного вектора, що відповідає від‘ємному ![]() . Прямі I і II називаються сепаратрисами сідла. На рис.1б стрілками показаний напрямок руху вздовж траєкторії при зростанні
. Прямі I і II називаються сепаратрисами сідла. На рис.1б стрілками показаний напрямок руху вздовж траєкторії при зростанні ![]() . Сепаратриса II є єдиною траєкторією, якій відповідає розв’язок, що прямує до 0 при
. Сепаратриса II є єдиною траєкторією, якій відповідає розв’язок, що прямує до 0 при ![]() . Тільки дві траєкторії I і II є прямолінійними. Інші траєкторії криволінійні й зі зростанням
. Тільки дві траєкторії I і II є прямолінійними. Інші траєкторії криволінійні й зі зростанням ![]() йдуть із
йдуть із ![]() в
в ![]() . Сепаратриси I і II розділяють фазову площину на 4 області, у яких лежать криволінійні траєкторії.
. Сепаратриси I і II розділяють фазову площину на 4 області, у яких лежать криволінійні траєкторії.
Якщо розв’язки ![]() комплексні з дійсною частиною
комплексні з дійсною частиною ![]() , відмінною від нуля, то особлива точка - фокус (рис.1, в), причому стійкий, якщо
, відмінною від нуля, то особлива точка - фокус (рис.1, в), причому стійкий, якщо ![]() й нестійкий, якщо
й нестійкий, якщо ![]() . На рис.1в стрілками показаний напрямок руху при зростанні
. На рис.1в стрілками показаний напрямок руху при зростанні ![]() у випадку стійкого фокуса.
у випадку стійкого фокуса.
Зауваження. У випадку фокуса траєкторії можуть бути закручені навколо (0,0) у різних напрямках. Для того, щоб визначити напрямок закручування, досить обчислити вектор швидкості ![]() в якій-небудь точці, наприклад, в (0,1). Аналогічно досліджується напрямок руху у випадку центра й виродженого вузла.
в якій-небудь точці, наприклад, в (0,1). Аналогічно досліджується напрямок руху у випадку центра й виродженого вузла.
Якщо розв’язки ![]() комплексні чисто мнимі (
комплексні чисто мнимі (![]() ), то особлива точка - центр (рис.1, г). Центр є стійкою, але не асимптотично стійкою точкою спокою.
), то особлива точка - центр (рис.1, г). Центр є стійкою, але не асимптотично стійкою точкою спокою.
Якщо розв’язки рівні й ненульові (тобто ![]() ), то особлива точка може бути виродженим вузлом (рис.1, д) або дикритичним вузлом (рис.1, е), причому дикритичний вузол має місце тільки у випадку системи
), то особлива точка може бути виродженим вузлом (рис.1, д) або дикритичним вузлом (рис.1, е), причому дикритичний вузол має місце тільки у випадку системи ![]() (або рівняння
(або рівняння ![]() ), а у всіх інших випадках при
), а у всіх інших випадках при ![]() особлива точка є виродженим вузлом. У випадку виродженого вузла всі траєкторії дотикаються однієї прямої, спрямованої вздовж єдиного власного вектора, що відповідає
особлива точка є виродженим вузлом. У випадку виродженого вузла всі траєкторії дотикаються однієї прямої, спрямованої вздовж єдиного власного вектора, що відповідає ![]() . Дикритичний вузол може бути стійким
. Дикритичний вузол може бути стійким ![]() і нестійким
і нестійким ![]() .
.
Якщо ж один або обидва розв’язки рівняння (5) дорівнюють нулю, то ![]() , і, отже, дріб у правій частині рівняння (4) скорочується. Рівняння набуває вигляду
, і, отже, дріб у правій частині рівняння (4) скорочується. Рівняння набуває вигляду ![]() , і розв’язок на площині XOY зображуються паралельними прямими.
, і розв’язок на площині XOY зображуються паралельними прямими.
2. Задача 1
Дослідити особливі точки рівняння. Накреслити інтегральні криві на площині XOY:
![]()
Розв’язання.
Для дослідження особливої точки рівняння
![]()
треба знайти розв’язок характеристичного рівняння
![]()
У нас ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Складаємо характеристичне рівняння
. Складаємо характеристичне рівняння
![]()
і розв’язуємо його відносно ![]()
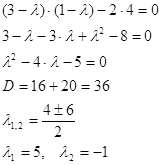
Розв’язки характеристичного рівняння дійсні й мають різні знаки.
Отже, особлива точка (0,0) - сідло. Сідло є нестійкою точкою спокою.
Похожие работы
... за допомогою центральних різниць. Якщо область має форму кола, зручно користуватись полярними координатами Наведемо деякі загальні зауваження. При чисельному розв’язанні крайових задач для диференціальних рівнянь в частинних похідних методом сіток можуть бути використані тільки різницеві схеми, які збігаються, оскільки в цьому разі можна розраховувати на отримання наближеного розв’язку задачі, ...
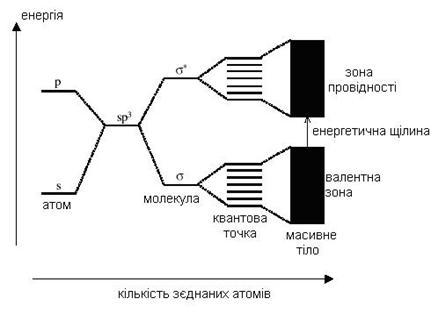
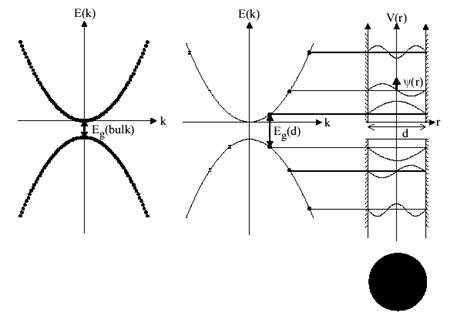
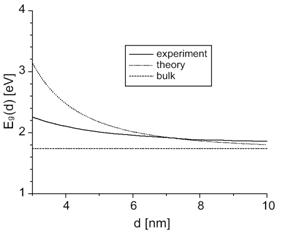
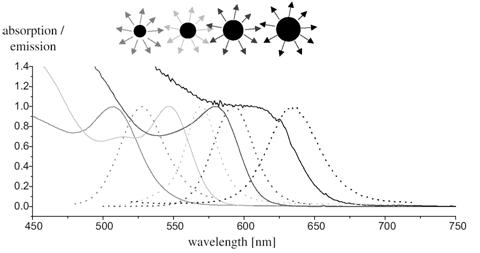
... ість зразків з таким високим контролем розміру квантової точки, форми та монодисперсності, щоб одночастинкові властивості не усереднювалися неоднорідністю зразка. До цих пір ансамблі квантових точок, вироблених з використанням найкращих технологій, все ще залежать від розмірів, але ця область розвивається дуже швидко. Різні технології та методи призводять до різних типологій квантових точок. ...
... Дотримання цих умов обов’язкове для покупця жінки. Спробуємо тепер перевірити правильність наших висновків. Звернемося до історії, оскільки вона зберегла до нас дані щодо правового становища заміжньої жінки, заснованого в стародавності на викраденні, давнині, купівлі й інших способах. Найдавніша історія скупа у своїх свідченнях. Дещо зберегла вона для нас із глибокої давнини. Але і це дещо часто ...
... розробити модель впливу зовнішнього середовища на фінансову стабільність банку; § виконати економіко-математичне моделювання фінансової стабільності; § запропонувати підвищення ефективності діяльності банку на основі економіко-математичного моделювання внутрішніх та зовнішніх факторів; § розробити інформаційну систему, на основі якої буде легко виконувати розрахунки при подальшому ...


0 комментариев