Навигация
Перший спосіб побудови інтегральних кривих
10321
знак
0
таблиц
7
изображений
1. Перший спосіб побудови інтегральних кривих.
Власний вектор 
, що відповідає власному числу 
, знаходимо, підставляючи в рівняння
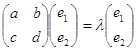
значення 
. Маємо
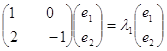
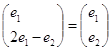
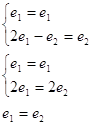
Власний вектор (1,1) матриці коефіцієнтів даної системи, відповідає власному числу 
.
Власний вектор , що відповідає власному числу 
, знаходимо, підставляючи в рівняння
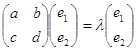
значення 
. Маємо
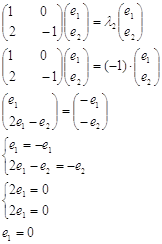
Власний вектор (0, 
) матриці коефіцієнтів даної системи, відповідає власному числу 
.
На площині 
будуємо прямі, спрямовані вздовж власних векторів (1;
1) і (0, ), а потім будуємо гіперболи.
2. Другий спосіб побудови інтегральних кривих.
Знайдемо сепаратриси сідла, тобто прямі, що розділяють гіперболи різних типів, які є фазовими кривими системи (тобто асимптоти цих гіпербол). Розділивши друге рівняння вихідної системи на перше рівняння, одержуємо
або 
Прямі, що проходять через особливу точку (0,0) шукаємо у вигляді 
(а також 
). Підставляючи в останнє рівняння, одержуємо
Виходить, що 
і - шукані прямі.
3. Напрямок руху по траєкторіях.
Для з'ясування напрямку руху по траєкторіях досить побудувати в якій-небудь точці 
вектор швидкості 
. Наприклад, у точці 
вектор швидкості дорівнює
,
у точці 
вектор швидкості
,
у точці 
вектор швидкості
,
у точці 
вектор швидкості
.
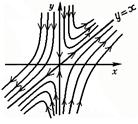
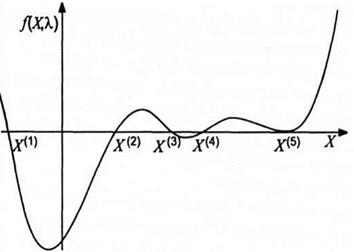
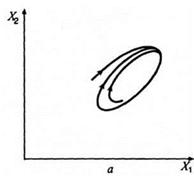
Рис.5. Положення рівноваги й інтегральні криві [6]
Список використаних джерел
1. Боярчук А.К., Головач Г.П. Дифференциальные уравнения в примерах и задачах. Справочное пособие по высшей математике. - М.: Эдиториал УРСС, 2001. - 384 с.
2. Васильева А.Б., Медведев Г.Н., Тихонов Н.А., Уразгильдина Т.А. Дифференциальные и интегральные уравнения, вариационное исчисление в примерах и задачах. - М.: ФИЗМАТЛИТ, 2003. - 432 с.
3. Немыцкий В.В., Степанов В.В. Качественная теория дифференциальных уравнений. - М.: Государственное издание техникотеоретической литературы, 1947. - 448 с.
4. Самойленко А.М., Кривошея С.А., Перестюк Н.А. Дифференциальные уравнения: примеры и задачи. Учеб. пособие. - 2е изд., перераб. - М.: Высш. шк., 1989. - 383 с.: ил.
5. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. - Ижевск, НИЦ "Регулярная и хаотическая динамика", 2000. - 176 с.
Похожие работы
... за допомогою центральних різниць. Якщо область має форму кола, зручно користуватись полярними координатами Наведемо деякі загальні зауваження. При чисельному розв’язанні крайових задач для диференціальних рівнянь в частинних похідних методом сіток можуть бути використані тільки різницеві схеми, які збігаються, оскільки в цьому разі можна розраховувати на отримання наближеного розв’язку задачі, ...
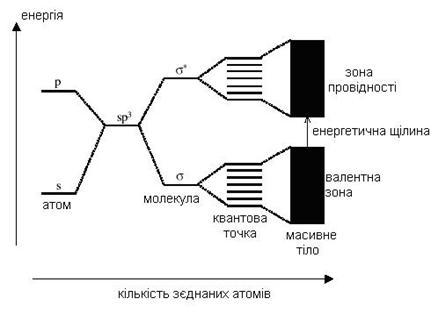
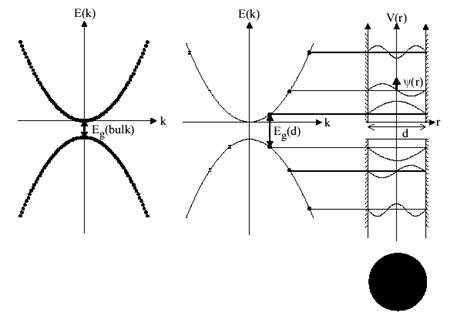
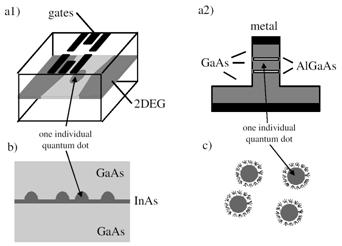
... ість зразків з таким високим контролем розміру квантової точки, форми та монодисперсності, щоб одночастинкові властивості не усереднювалися неоднорідністю зразка. До цих пір ансамблі квантових точок, вироблених з використанням найкращих технологій, все ще залежать від розмірів, але ця область розвивається дуже швидко. Різні технології та методи призводять до різних типологій квантових точок. ...
... Дотримання цих умов обов’язкове для покупця жінки. Спробуємо тепер перевірити правильність наших висновків. Звернемося до історії, оскільки вона зберегла до нас дані щодо правового становища заміжньої жінки, заснованого в стародавності на викраденні, давнині, купівлі й інших способах. Найдавніша історія скупа у своїх свідченнях. Дещо зберегла вона для нас із глибокої давнини. Але і це дещо часто ...
... розробити модель впливу зовнішнього середовища на фінансову стабільність банку; § виконати економіко-математичне моделювання фінансової стабільності; § запропонувати підвищення ефективності діяльності банку на основі економіко-математичного моделювання внутрішніх та зовнішніх факторів; § розробити інформаційну систему, на основі якої буде легко виконувати розрахунки при подальшому ...
0 комментариев