Навигация
Построим графики (полигон и гистограмму) полученного ряда распределения. Для этого используем графический метод
2. Построим графики (полигон и гистограмму) полученного ряда распределения. Для этого используем графический метод.
Для построения полигона и гистограммы необходимо определить срединное значение интервала затрат на рубль продукции по формуле:
![]() ,
,
где SН — нижняя граница интервала;
SВ — верхняя граница интервала.
Таблица 5 Определение срединного значения интервала
| Группы предприятий по затратам на рубль продукции, руб. | Срединное значение интервала, руб. | Количество предприятий |
| 0,77-0,79 | 0,78 | 6 |
| 0,79-0,81 | 0,80 | 5 |
| 0,81-0,83 | 0,82 | 8 |
| 0,83-0,85 | 0,84 | 7 |
| 0,85-0,87 | 0,86 | 4 |
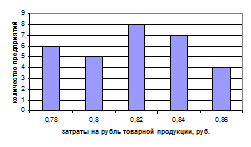
Рис. 1. Гистограмма затрат на рубль продукции
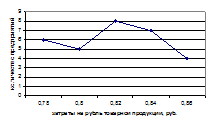
Рис. 2. Полигон затрат на производство
Мода и медиана могут быть определены графически: первая – по гистограмме, а вторая по кумуляте.
Определим моду по гистограмме (рис. 1). В прямоугольнике, имеющем наибольшую высоту, проводим две линии, как показано на рис.3, и из точки их пересечения опускаем перпендикуляр на ось абсцисс. Значение х на оси абсцисс. Значение х на оси абсцисс в этой точке есть мода (Мо). Согласно рис. 3 Мо » 0,82 руб. То есть большинство единиц совокупности имеют затраты на единицу продукции выше 0,82 руб.
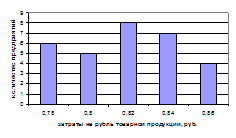
Рис. 3. Графическое определение моды
Для графического отыскания медианы по накопленным частотам строим кумуляту. Для этого из верхней границы каждого интервала на оси абсцисс восстанавливаем перпендикуляр, соответствующий по высоте накопленной частоте с начала ряда по данный интервал. Соединив последовательно вершины перпендикуляров, получим кривую, называемую кумулятой (рис. 4).
Таблица 6 Определение накопленных частот
| Группы предприятий по затратам на рубль продукции, руб. | Срединное значение интервала, руб. | Количество предприятий | Накопленные частоты |
| 0,77-0,79 | 0,78 | 6 | 6 |
| 0,79-0,81 | 0,80 | 5 | 11 |
| 0,81-0,83 | 0,82 | 8 | 19 |
| 0,83-0,85 | 0,84 | 7 | 26 |
| 0,85-0,87 | 0,86 | 4 | 30 |
| Итого | х | 30 |
![]()
![]()
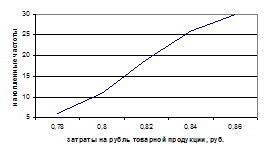
Рис. 4. Кумулята распределения 30 предприятий по затратам на рубль продукции (графическое определение медианы)
Из точки на оси ординат, соответствующей половине всех частот (порядковому номеру медианы), проводим прямую, параллельную оси абсцисс, до пересечения ее с кумулятурой. Опустив из этой точки перпендикуляр на ось абсцисс, находим значение медианы (Ме). Судя по рис. 4 Ме » 0,81 руб.
3. Далее рассчитаем характеристики интервального ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации.
Таблица 7 Данные для расчета показателей вариации
| Группы предприятий по затратам на рубль продукции, руб. | Число предприятий | Расчетные показатели | |||
| fi | xi (ср. значение интервала) | хifi | (хi – | (хi – | |
| 0,77-0,79 | 6 | 0,78 | 4,68 | -0,04 | 0,009 |
| 0,79-0,81 | 5 | 0,80 | 4,00 | -0,02 | 0,002 |
| 0,81-0,83 | 8 | 0,82 | 6,56 | 0,00 | 0,000 |
| 0,83-0,85 | 7 | 0,84 | 5,88 | 0,02 | 0,003 |
| 0,85-0,87 | 4 | 0,86 | 3,44 | 0,04 | 0,007 |
| Итого | 30 | х | 24,56 | 0,007 | 0,021 |
Вычислим средние затраты на рубль продукции по формуле средней арифметической взвешенной, так как даны частоты усредняемой величины:
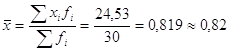 руб.
руб.
Далее вычислим дисперсию.
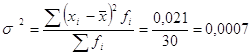 руб.
руб.
Среднее квадратическое отклонение найдем как по формуле:
![]() руб.
руб.
Далее определим коэффициент вариации:
![]() .
.
Таким образом, колеблемость количества предприятий от среднего значения составляет 3,2 %, это незначительный коэффициент вариации и следовательно, совокупность устойчива и средняя величина является типичной для всей совокупности.
4. Вычислим среднюю арифметическую по исходным данным. Так как здесь не даны частоты изучаемого явления, то средняя будет определяться как средняя арифметическая простая по формуле:
![]() ,
,
где х — затраты на рубль продукции, руб.;
n — количество предприятий.
Тогда ![]() руб.
руб.
Эта средняя ниже полученной в п.3, так как здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина:
![]()
3. Задание 2 расчетной части
По исходным данным:
1. Установите наличие и характер связи между выпуском продукции и уровнем затрат на рубль продукции, образовав пять групп с равными интервалами по обоим признакам, методами:
а) аналитической группировки;
б) корреляционной таблицы.
Решение
а) Для анализа группировки построим аналитическую таблицу (табл. 8).
Таблица 8
Зависимость между выпуском продукции и уровнем затрат на рубль продукции
| № п/п | Группы предприятий по уровню затрат на рубль продукции | Количество предприятий | Затраты рубль продукции, руб. | Выпуск продукции, млн. руб. | ||
| всего | в среднем на 1 предприятие | всего | в среднем на 1 предприятие | |||
| А | Б | 1 | 2 | 3=2 / 1 | 4 | 5 = 4/1 |
| 1 | 0,77-0,79 | 6 | 4,69 | 0,782 | 399,272 | 66,545 |
| 2 | 0,79-0,81 | 5 | 4,02 | 0,804 | 256,875 | 51,375 |
| 3 | 0,81-0,83 | 8 | 6,55 | 0,819 | 346,374 | 43,297 |
| 4 | 0,83-0,85 | 7 | 5,86 | 0,837 | 235,159 | 33,594 |
| 5 | 0,85-0,87 | 4 | 3,44 | 0,860 | 82,860 | 20,715 |
| Всего | 30 | 24,56 | 0,819 | 1320,540 | 44,018 | |
Анализ данной таблицы показывает, что при снижении выпуска продукции в стоимостном выражении затраты на рубль продукции пропорционально возрастают. Таким образом, связь между признаками имеется. Связь обратная.
2. Определим зависимость между признаками методом построения корреляционной таблицы. Для ее построения нужно сгруппировать предприятия по выпуску продукции в 5 групп с равными интервалами, аналогично вышеизложенному алгоритму (см. лист расчетов в MS Excel — файл «книга1»).
Таблица 9 Корреляционная таблица
| Группы предприятий по затратам на рубль продукции | Срединное значение интервалов Хi | Группировка предприятий по выпуску продукции | Всего | Групповая средняя Уj | ||||
| 14,4-27,36 | 27,36-40,32 | 40,32-53,28 | 53,28-66,24 | 66,24-79,20 | ||||
| Срединное значение Уj | ||||||||
| 19,08 | 33,84 | 46,80 | 59,76 | 72,72 | ||||
| 0,77-0,79 | 0,78 | — | — | — | — | 3 | 3 | 0,78 |
| 0,79-0,81 | 0,80 | — | — | — | 6 | — | 6 | 0,80 |
| 0,81-0,83 | 0,82 | — | — | 9 | — | — | 9 | 0,82 |
| 0,83-0,85 | 0,84 | — | 8 | — | — | — | 8 | 0,84 |
| 0,85-0,87 | 0,86 | 4 | — | — | — | — | 4 | 0,86 |
| Всего | — | 4 | 8 | 9 | 6 | 3 | 30 | — |
| Групповая средняя Хi | — | 19,08 | 33,84 | 46,8 | 59,76 | 72,72 | — | |
Для определения и характеристики взаимосвязи между двумя изучаемыми признаками следует построить корреляционное поле (по срединным значениям интервалов).
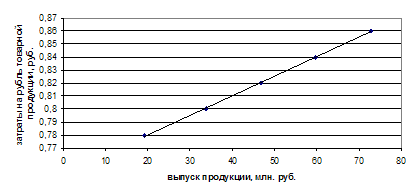
Рис. 5. Корреляционное поле зависимости выпуска продукции от затрат на рубль продукции
Таким образом, метод построения корреляционной таблицы показывает, что связь между анализируемыми признаками имеется, связь эта линейная, зависимость между признаками обратная, то есть при увеличении уровня затрат на выпуск продукции, выпуск продукции в стоимостном выражении уменьшается.
4. Задание 3 расчетной части
По результатам выполнения задания 1 с вероятностью 0,683 определите:
1. Ошибку выборки среднего уровня затрат на рубль продукции и границы, в которых будет находиться средний уровень затрат на рубль продукции в генеральной совокупности.
2. Ошибку выборки доли организаций с уровнем затрат на рубль продукции 0,83 руб. и более и границы, в которых будет находиться генеральная доля.
1. При расчете средней ошибки механического бесповторного отбора пользуются формулой:
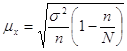 ,
,
где ![]() — выборочная дисперсия;
— выборочная дисперсия;
n — число единиц выборочной совокупности;
N — число единиц генеральной совокупности.
В п. 3 задания 1 ![]() руб.; n = 30;
руб.; n = 30; ![]() .
.
Тогда ![]() руб.
руб.
Предельная ошибка выборочной средней с вероятностью 0,683 (гарантийный коэффициент ![]() ) составит:
) составит:
![]() руб.
руб.
Верхняя граница генеральной средней:
![]() руб.
руб.
Нижняя граница генеральной средней:
![]() руб.
руб.
Таким образом, с вероятностью 0,683 можно утверждать, что средний размер уровня затрат на рубль продукции в генеральной совокупности колеблется в пределах ![]() руб.
руб.
2. Доля предприятий в выборочной совокупности с уровнем затрат на рубль продукции 0,83 руб. и более составляет:
![]() ,
,
где m — количество предприятий, удовлетворяющих условию (предприятия 4 и 5 интервалов).
![]() или 40 %
или 40 %
Предельная ошибка доли с вероятностью 0,683 (гарантийный коэффициент![]() ) при бесповторном отборе определяется по формуле:
) при бесповторном отборе определяется по формуле:
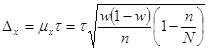 .
.
Подставив имеющиеся значения, получим:
![]() или 8 %.
или 8 %.
С вероятностью 0,683 при бесповторном отборе доля предприятий с уровнем затрат на рубль продукции 0,83 руб. и более в генеральной совокупности находится в пределах:
р = 40 % ± 8 % или 32 % ≤ р ≤ 48 %.
5. Задание 4 расчетной части
Имеются следующие данные по организации:
Таблица 10 Исходные данные к задаче
| Вид продукции | Базисный год | Отчетный год | ||||
| Выпуск продукции, тыс. шт. | Себестоимость единицы продукции, руб. | Отпускная цена за единицу продукции, руб. | Выпуск продукции, тыс. шт. | Себестоимость единицы продукции, руб. | Отпускная цена за единицу продукции, руб. | |
| А | 40 | 210 | 262,5 | 48 | 180,0 | 255,0 |
| Б | 28 | 350 | 425,0 | 25 | 340,0 | 414,0 |
| В | 15 | 280 | 372,0 | 16 | 300,0 | 365,0 |
Определите:
Похожие работы
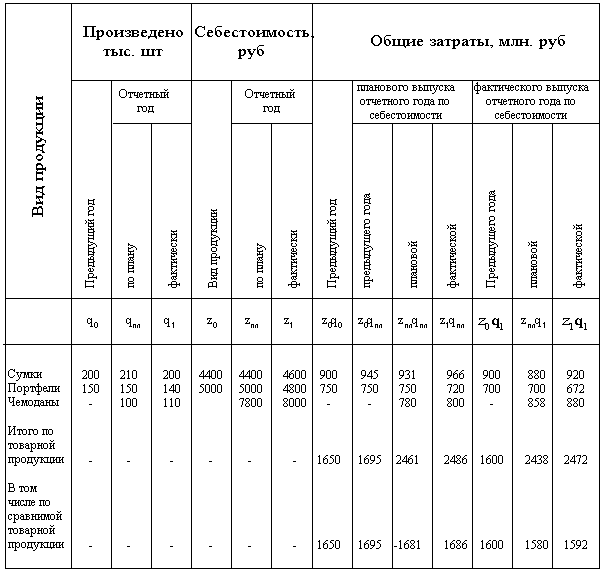
... в отчетном периоде по сравнению с базисным увеличились на 4,68% 3. Аналитическая часть В этой части работы изложены результаты проведенного статистического исследования изменения уровня затрат на рубль товарной продукции организаций. Изучение проводилось средствами пакета программ MS Excel. 3.1 Постановка задачи Произвести исследование изменения уровня затрат на рубль товарной ...
... в сумме 2472-2438=34 млн руб., в том числе по несравнимой продукции: 880-858=22 млн руб. Выпуск и себестоимость продукции на кожгалантерейной фабрике 1.4 Статистические методы изучения уровней динамики Основная цель статистического изучения динамики коммерческой деятельности состоит в выявлении и измерении закономерностей их развития во времени. Это достигается посредством построения и ...
... управления затратами на основе поиска резервов, способной решать проблемы эффективного использования внутрихозяйственных факторов снижения затрат с помощью методов их выявления, анализа и планирования. 2.2 Методика расчета анализа затрат на рубль товарной продукции Для практического использования в системе управления формированием затрат и издержек целесообразно выделить и рассмотреть ...
... себестоимости по видам затрат и выявляет влияние изменения структуры на динамику себестоимости; 2) дает обобщающую характеристику динамики себестоимости продукции; 3) исследует факторы, определяющие уровень и динамику себестоимости, и выявляет возможности ее снижения. 1.2. Статистическое изучение структуры себестоимости. Необходимость изучения структуры себестоимости диктуется тем ...








0 комментариев