Показатели финансового менеджмента
Риск-менеджмент
Классификация предпринимательского риска
Финансовое прогнозирование на предприятиях
Задачи, этапы и методы финансового прогнозирования
Содержание отчета о движении денежных средств (ДДС)
Способы составления отчета о движении денежных средств
Математические основы финансового менеджмента
Начисление процентов при регулярных взносах
Учет денежных обязательств
Вторая концепция эффекта финансового рычага
Тактический финансовый менеджмент
Наращивание оборота за счет самофинансирования
Навигация
Математические основы финансового менеджмента
Финансовый менеджмент
113708
знаков
13
таблиц
6
изображений
4. Математические основы финансового менеджмента
4.1 Начисление простых ставок ссудных процентов
Процентными деньгами (процентами) называют сумму доходов от представления денег в долг в различных формах (открытие депозитных счетов, выдача кредитов, покупка облигаций и др.) Сумма процентных денег зависит от суммы долга, срока его выплаты и процентной ставки. Проценты могут выплачиваться по мере их начисления или присоединяться к сумме долга. Увеличение суммы долга за счет присоединения начисленных процентов называют наращением (ростом) первоначальной суммы долга. Отношение наращенной суммы к первоначальной сумме долга называют множителем (коэффициентом) наращения. Интервал времени, за который начисляют проценты, называют периодом начисления.
При использовании простых процентов сумма процентных денег в течение всего срока долга определяется исходя из первоначальной суммы долга независимо от количества периодов начисления и их длительности. Простая годовая ставка процентов определяется как
(21)
где i(%) – простая годовая ставка процентов, %;
Ir – сумма процентных денег, выплачиваемая за r-ый год;
Р – первоначальная сумма долга.
Чаще всего при проведении расчетов обычно используют относительное значение ставки процентов (i):
(22)
Сумма процентных денег, выплачиваемая за год равна:
(23)
Если срок долга составляет n лет, то общая сумма процентных денег (I) будет равна:
(24)
Сумма долга с начисленными процентами (S) будет определяться выражением:
(25)
Если срок хранения вклада выражается в днях в формулу (24) следует подставить выражение:
(26)
где К¢ – срок хранения вклада в днях;
К – количество дней в году.
Срок вклада в днях и расчетное количество дней в году при начислении процентов определяется по-разному. В так называемой германской практике подсчет числа дней основывается на длительности года в 360 дней и месяцев в 30 дней. При французской практике длительность года принимается равной 360 дням, а количество дней в месяцах берется равным их фактической календарной длительности (28, 29, 30 и 31). При английской практике берутся год в 365 дней и соответствующая точная длительность месяцев.
Из формулы (25) можно при прочих заданных условиях определить срок вклада в годах:
(27)
или срок вклада в днях:
(28)
Из формулы (25) можно также определить ставку простых процентов при прочих заданных условиях:
(29)
Используя формулу для наращенной суммы (25), можно решать обратную задачу – определять сумму вклада при заданных значениях суммы вклада с начисленными процентами и ставки процентов:
(30)
Рассмотренную операцию называют дисконтированием по простой ставке процентов. Дисконтирование позволяет учитывать в финансово-экономических расчетах фактор времени. Выражение (30) можно также записать в виде:
(31)
где Kq – коэффициент дисконтирования.
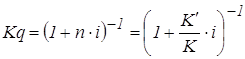(32)
Таким образом, коэффициент дисконтирования является обратной величиной множителя (коэффициента) наращения.
4.2 Начисление сложных ставок ссудных процентов
При начислении сложных процентов процентные деньги, начисленные после первого периода начисления, являющегося частью общего срока хранения вклада, не выплачиваются, а присоединяются к сумме вклада. На втором периоде начисления проценты будут начисляться исходя из первоначальной суммы вклада, увеличенной на сумму процентов, начисленных после первого периода начисления, и так далее на каждом последующем периоде начисления. Если проценты за период начисления начисляются по постоянной сложной ставке i и все периоды начисления имеют одинаковую длительность суммы вклада с процентами в конце первого периода (S1) будет равна:
(33)
Сумма вклада с процентами в конце второго периода (S2) будет соответственно равна:
(34)
Если в течение срока хранения вклада будет N одинаковых периодов начисления, сумма вклада с процентами в конце срока (S) составит:
(35)
Сумма начисленных процентов будет равна:
(36)
Начисление сложных процентов может осуществляться несколько раз в году (например по месяцам, кварталам, полугодиям). В этих случаях указывается либо ставка процентов за период, либо годовая ставка процентов, исходя из которой, определяется ставка процентов за период начисления, иными словами, номинальная ставка процентов.
Сумма вклада с процентами (наращенная сумма) при сроке n лет в этих случаях будет равна:
(37)
где j – номинальная годовая ставка процентов;
m – количество периодов начисления в году;
N – количество периодов начисления в течение срока хранения вклада:
Сумма начисленных процентов составит:
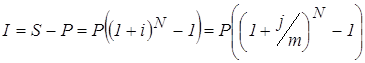(38)
Из формул для наращенной суммы при начислении сложных процентов один или несколько раз в году (35, 37) можно получить выражение для срока хранения вклада при заданных условиях. При использовании сложной годовой ставки процентов срок хранения в годах будет равен:
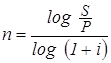(39)
Из формул (35, 37) можно также определить ставку сложных процентов при прочих заданных условиях:
(40)
Из тех же формул можно также определить значение первоначальной суммы вклада, или, иначе говоря, осуществить дисконтирование будущей суммы вклада с процентами S по сложной ставке процентов. При использовании годовой ставки сложных процентов i и сроке хранения вклада n лет дисконтированное значение будущей суммы вклада с процентами будет равно:
(41)
где Kq – коэффициент дисконтирования (приведения):
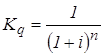(42)
Похожие работы
... (2.2.44) Сложная номинальная процентная ставка (j) (2.2.45) (2.2.46) Сложная учетная ставка (dсл) (2.2.47) (2.2.48) – По мере усложнения задач, стоящих перед финансовым менеджментом, сфера применения непрерывных процентов будет расширяться, так как при этом становится возможным использовать ...
... 37,308 R19992= 2,227 R1997= 9,159 R1998= 6,108 R1999= 1,492 ГЛАВА 4. РЕКОМЕНДАЦИИ ПО СОВЕРШЕНСТВОВАНИЮ ФИНАНСОВОГО МЕНЕДЖМЕНТА ОРГАНИЗАЦИИ 4.1. Направления совершенствования финансового менеджмента Управление финансами стало важнейшей сферой деятельности любого субъекта социально-рыночного хозяйства, ...
... организации высокоэффективного управления его финансами. Такое управление финансами отдельных субъектов хозяйствования выделилось в странах с рыночной экономикой в начале XX века в специальную область знаний, которая получила название “финансовый менеджмент”. Он представляет собой процесс управления формированием, распределением и использованием финансовых ресурсов хозяйствующего субъекта и ...
... предприятия; · самофинансирования, · материальной заинтересованности, · материальной ответственности, · обеспеченности рисков финансовыми резервами. II. Базовые концепции финансового менеджмента 2.1 Концепция временной стоимости денег Концепция изменения стоимости денег во времени играет центральную роль в практике финансовых вычислений и ...
0 комментариев