Навигация
Начисление процентов при регулярных взносах
4.3 Начисление процентов при регулярных взносах
Если взносы вносятся регулярно одинаковыми суммами через одинаковые периоды, можно сразу определить сумму вклада с начисленными процентами и сумму начисленных процентов за весь срок. Например, если ежегодно в конце каждого года в течение n лет на депозитный счет будет поступать сумма R, а проценты на хранящуюся сумму будут начисляться по сложной годовой ставке i, суммы последовательных взносов с процентами, срока хранения вклада, по формуле (35) будет равны:
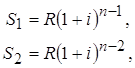
…
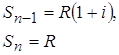
Применив к сумме всех значений St(t = 1, 2,…, n) формулу для суммы членов геометрической прогрессии, получаем:
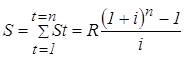 (43)
(43)
Последовательность денежных поступлений, осуществляемых равными суммами через равные периоды, называют постоянной финансовой рентой или аннуитетом, а сумму всех таких поступлений – наращенной величиной финансовой ренты.
Если взносы в размере R будут вноситься P раз в году в конце расчетных периодов, на суммы на счете m раз в году будут начисляться сложные проценты по номинальной годовой ставке j, выражение для суммы всех взносов с начисленными процентами за n лет, которое можно аналогичным образом, будет иметь вид:
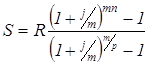 (44)
(44)
Из формул для наращенной суммы последовательности взносов (43) и (44) можно определить размеры взносов при прочих заданных условиях:
![]() (45)
(45)
или 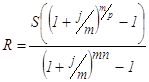 (46)
(46)
Если одинаковые суммы R будут поступать на депозитный счет в начале каждого года, то сумма всех поступлений с начисленными процентами через n лет, определяемая аналогичным образом, будет равна:
![]() (47)
(47)
Если взносы в размере R будут вноситься на депозитный счет P раз в году в начале каждого расчетного периода, и на них m раз в году будут начисляться сложные проценты по номинальной годовой ставке j, сумма всех взносов с начисленными процентами через n лет будет равна:
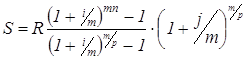 (48)
(48)
Из формул (47) и (48) можно определить размер взносов при прочих заданных условиях:
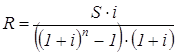 (49)
(49)
или
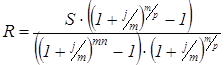 (50)
(50)
4.4 Расчет эффективной годовой ставки процентов
Банки и финансовые компании объявляют самые различные условия начисления процентов по вкладам. Таким образом, возникает необходимость сравнивать условия привлечения вкладов по некоторому общему показателю. В качестве такого показателя обычно используется эквивалентная (эффективная) годовая ставка простых или сложных процентов.
Доходность краткосрочных (до года) вкладов может быть определена по эффективной ставке простых процентов аналогично формуле (29), в числитель которой следует подставлять значение суммы начисленных процентов, определяемое в соответствии с конкретными условиями их начисления. Если в объявлениях банка говорится, что вклады принимаются с ежемесячной (ежеквартальной) выплатой процентов без указания на их присоединение к сумме основного вклада, это означает, что используются простые проценты с годовой ставкой:
![]() (51)
(51)
где I – сумма процентов, начисленных за период начисления;
P – сумма вклада;
n – длительность периода начисления в годах.
Отношение I к P представляет собой ставку процентов за период начисления. Следовательно, эффективная ставка процентов будет равна:
![]() (52)
(52)
где N – количество периодов начисления в году.
Если на вклады начисляются сложные проценты несколько раз в году, эффективная годовая ставка процентов может быть определена исходя из условия, что полученный доход (сумма процентов) I будет равен доходу, который был бы получен при размещении той же самой суммы P на тот же срок n по эффективной годовой ставке простых процентов iэ:
![]() (53)
(53)
Следовательно, эффективная годовая ставка процентов будет определяться соотношением:
![]() (54)
(54)
По формуле (38) доход, получаемый при начислении сложных процентов несколько раз в году, будет равен:
![]() (55)
(55)
Эффективная годовая ставка процентов в соответствии с соотношением (55) будет определятся формулой:
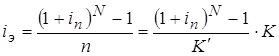 (56)
(56)
Значение ставки процентов за период начисления может задаваться непосредственно или определяться на основе заданного значения номинальной годовой ставки процентов. При этом значение эффективной годовой ставки процентов, соответствующее заданному значению номинальной годовой ставки j, по формуле (56) при n=1 и N= m будет равно:
 (57)
(57)
Похожие работы
... (2.2.44) Сложная номинальная процентная ставка (j) (2.2.45) (2.2.46) Сложная учетная ставка (dсл) (2.2.47) (2.2.48) – По мере усложнения задач, стоящих перед финансовым менеджментом, сфера применения непрерывных процентов будет расширяться, так как при этом становится возможным использовать ...
... 37,308 R19992= 2,227 R1997= 9,159 R1998= 6,108 R1999= 1,492 ГЛАВА 4. РЕКОМЕНДАЦИИ ПО СОВЕРШЕНСТВОВАНИЮ ФИНАНСОВОГО МЕНЕДЖМЕНТА ОРГАНИЗАЦИИ 4.1. Направления совершенствования финансового менеджмента Управление финансами стало важнейшей сферой деятельности любого субъекта социально-рыночного хозяйства, ...
... организации высокоэффективного управления его финансами. Такое управление финансами отдельных субъектов хозяйствования выделилось в странах с рыночной экономикой в начале XX века в специальную область знаний, которая получила название “финансовый менеджмент”. Он представляет собой процесс управления формированием, распределением и использованием финансовых ресурсов хозяйствующего субъекта и ...
... предприятия; · самофинансирования, · материальной заинтересованности, · материальной ответственности, · обеспеченности рисков финансовыми резервами. II. Базовые концепции финансового менеджмента 2.1 Концепция временной стоимости денег Концепция изменения стоимости денег во времени играет центральную роль в практике финансовых вычислений и ...







0 комментариев