Навигация
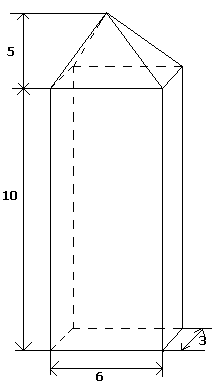
Вычислить объем башни, размеры которой в метрах даны на рисунке 10
88628
знаков
4
таблицы
18
изображений
3. Вычислить объем башни, размеры которой в метрах даны на рисунке 10.
Вывод формулы объема пирамиды в учебнике [7] рассматривается в два этапа (Приложение 7). Вначале автор предлагает рассмотреть для треугольной пирамиды, а затем – для произвольной. Автор проводит ось, рассматривает сечение плоскостью, выражает площадь сечения через площадь основания, применяет основную формулу для вычисления объемов (определенный интеграл). В доказательстве автор также использует признаки подобия. Таким образом, хорошо прослеживается связь с ранее уже изученным.
Следствием теоремы, в отличие от [8], является формула объема для усеченной пирамиды. Доказательства в данном учебнике не приведено. В учебнике [7] формулировка формулы приведена, как задача, причем автор сам задачу решает.
Мы рассмотрели основные рекомендации для изучения данной темы, которые описаны в соответствующей литературе. Но есть и другие приемы и методы, которыми практически не пользуются, но они имеют свои преимущества. Далее приведена примерная (авторская) система данных уроков.
|
Дело в том, что объемы тел – тема, вызывающая достаточно большие трудности у учащихся. В этом разделе есть четыре трудных для усвоения теоремы: 1) об объеме прямоугольного параллелепипеда; 2) об объеме пирамиды; 3) об объеме цилиндра; 4) об объеме тела, полученного вращением криволинейной трапеции [21].
Выводы формул для вычисления объема каждого вида многогранника, цилиндра, конуса проводятся разными методами, что вызывает значительные трудности при их воспроизведении.
Предлагаемая мною система изучения этого раздела устраняет недостатки и создает условия для усвоения основной идеи измерения фигур в пространстве: объем фигуры может быть найден с помощью вычисления интеграла от определенным образом заданной функции.
С целью осуществления такого подхода к измерениям пространственных фигур предлагается посвятить несколько уроков обобщению изученного ранее материала об измерении отрезков и плоских фигур (о длинах и площадях) и ввести аналогичным образом измерение пространственных фигур. Рассмотрим их содержание более подробно.
Урок 1
Тема урока: обобщение свойства длин отрезков и площадей плоских фигур.
Цель урока: повторить свойства длин отрезков и площадей фигур, провести необходимые аналогии.
В начале урока необходимо повторить таблицу метрической системы мер длины, площади и объемов. Для этого удобно заготовить такую таблицу заранее (если ее нет в кабинете) и вывесить ее перед учениками (Приложение 4).
Упражнения для повторения свойств площадей фигур:
1. На рис. 11 изображен отрезок АВ. Найдите длину отрезка АВ, считая единицей измерения: а) сторону одной клетки; б) 1 см (отрезок CD); в) отрезок EF.
При решении этой задачи следует акцентировать внимание учащихся на том, что длина одного и того же отрезка может выражаться разными числами в зависимости от выбора единицы измерения. Но если единица измерения уже выбрана, то длина отрезка есть единственное число. При этом длина отрезка всегда положительна.
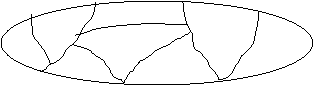
2. На рис. 12 изображена плоская фигура ABCDEF. Найдите ее площадь, приняв за единицу измерения: а)половину клетки; б) одну клетку; в) треугольник POQ.
При решении этой задачи следует обратить внимание учащихся на то, что площадь плоской фигуры есть число, которое зависит от выбора единицы измерения. Если единица измерения выбрана, то площадь фигуры единственна. Кроме того, площадь фигуры обязательно неотрицательна, какая бы фигура ни была взята в качестве единицы измерения.
|
|
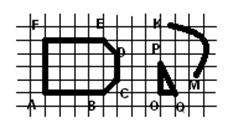
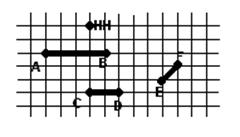Рис. 12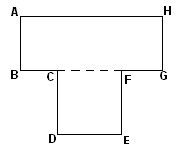 
3. Прямоугольник имеет стороны 5 и 4 см. Какова площадь прямоугольника? Какая фигура выбрана за единицу измерения площадей и какова его площадь?
4.
|
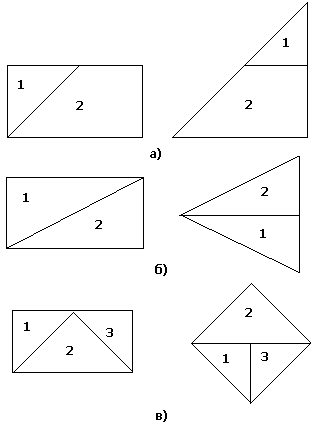
Решая эту задачу, мы пользуемся таким свойством площадей плоских фигур: если плоская фигура разбита на две, общая часть которых есть линия или точка, то площадь всей фигуры равна сумме площадей, ее составляющих.
5. 
Треугольники ABC и A1B1C1 конгруэнтны. Площадь 
ABC равна 36 см2. Какова площадь A1B1C1?
Решив этот комплекс задач, можно сделать выводы, сформулировав их как свойства измерения площадей плоских фигур.
Упражнение для закрепления:
Похожие работы
... подобраны опорные задачи, которые можно использовать на уроке при изучении данной темы. Таким образом, в данной работе были рассмотрены основные, общие моменты изучения многогранников в школьном курсе стереометрии. В следствие чего дальнейшие исследования могут проходить в направлении более детального изучения отдельных разделов данной темы, а также пропедевтического введения многогранников в ...
... . Позитивизма. Для позитивистов верным и испытанным является только то, что получено с помощью количественных методов. Признают наукой лишь математику и естествознание, а обществознание относят к области мифологии. Неопозитивизм, Слабость педагогики неопозитивисты усматривают в том, что в ней доминируют бесполезные идеи и абстракции, а не реальные факты. Яркий ...
... итог сказанному выше, можно утвердительно сказать о том, что поступление названных учебников «Моя математика» в школы даст возможность учителям начального звена обучения более системно и продуктивней осуществлять развитие пространственных представлений младших школьников. Заключение Из курсов педагогики и методики математики известно, что деятельность может быть репродуктивной и продуктивной. ...
... не разработана. В следующей главе мы выявим особенности и методики применения основных идей квантового обучения в обучении математике. Глава 2. Особенности применения квантового обучения при обучении математике 2.1. Реализация основных идей квантового обучения в преподавании математики Рассмотрим реализацию основных идей квантового обучения в преподавании математике в соответствии с разбиением ...
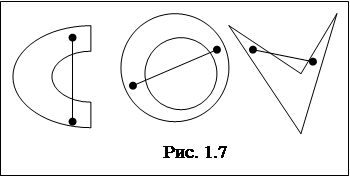
0 комментариев