Навигация
2. Актуализация знаний
Вы изучали геометрические построения на протяжении 7 и 8 классов. Вспомните, какие построения вы выполняли? Таким образом, вы знаете как выполнить построение:
1) отрезка, равного данному;
2) угла, равного данному;
3) биссектрисы угла;
4) перпендикулярных прямых;
5) середины отрезка;
6) треугольника по трем сторонам;
7) деление отрезка на n равных частей.
3. Изучение нового материала
Также вы строили серединный перпендикуляр к данному отрезку. Как вы это делали? (чертеж на доске)
Наверняка вы говорили о том, что на серединном перпендикуляре к данному отрезку находятся все точки, которые равноудалены от концов отрезка.
Говорят, что серединный перпендикуляр – это геометрическое место точек, равноудаленных от двух данных точек.
Геометрическим местом точек плоскости, обладающих данным свойством, называется множество всех точек плоскости, каждая из которых обладает этим свойством (запись определения в тетради).
Рассмотрим еще некоторые основные геометрические построения (раздаточный материал):
I. Геометрическое место точек, одинаково удаленных от данной точки (окружность).
II. Геометрическое место точек, одинаково удаленных от данной прямой (пара параллельных прямых).
III. Геометрическое место точек, равноудаленных от двух данных точек (серединный перпендикуляр к отрезку)
IV. Геометрическое место точек, равноудаленных от двух данных а) пересекающихся, б) параллельных прямых (пара перпендикулярных прямых в первом случае, прямая линия — во втором).
Существуют также более сложные ГМТ, которые используются при решении задач (раздаточный материал):
1) Геометрическое место вершин С треугольников, имеющих общее основание АВ, у которых боковая сторона АС равна данному отрезку.
2) Геометрическое место вершин С треугольников с общим основанием АВ, у которых медиана, проведенная к основанию, равна данному отрезку.
3) Геометрическое место центров окружностей данного радиуса, проходящих через данную точку.
4) Геометрическое место центров окружностей данного радиуса, касающихся данной окружности (внешним образом, внутренним образом).
5) Геометрическое место вершин треугольников с общим основанием, у которых высота, опущенная на это основание, равна данному отрезку.
6) Геометрическое место центров окружностей данного радиуса, касающихся данной прямой.
7) Геометрическое место центров окружностей данного радиуса, отсекающих на данной прямой хорду данной длины.
8) Геометрическое место середин отрезков, соединяющих данную точку со всеми точками данной прямой.
9) Геометрическое место вершин равнобедренных треугольников с общим основанием.
10) Геометрическое место центров окружностей, проходящих через две данные точки.
11) Геометрическое место центров окружностей, описанных около всех треугольников с общим основанием.
12) Геометрическое место центров окружностей, касающихся внешним образом (внутренним образом) двух равных окружностей.
13) Геометрическое место центров окружностей, касающихся двух данных (пересекающихся, параллельных) прямых.
14) Геометрическое место вершин прямоугольных треугольников с общей гипотенузой.
Теперь вспомните, как вы строили треугольник по трем сторонам (чертеж на доске).
Какие ГМТ здесь используются? Их пересечение дает нам третью вершину искомого треугольника. Оказывается, что при решении данной задачи вы использовали метод ГМТ.
Суть метода ГМТ заключается в следующем: сводят задачу к нахождению некоторой точки, которая определяется двумя условиями, вытекающими из требования задачи.
Допустим, геометрическим местом точек, удовлетворяющих первому условию, есть фигура F1, а геометрическим местом точек, удовлетворяющих второму условию, есть фигура F2. Тогда каждая точка пересечения этих двух геометрических мест удовлетворяет требованиям задачи. Например, построение треугольника по трем сторонам.
Таким образом, задача не будет иметь решений, если эти ГМТ не пересекаются. И будет иметь столько решений, сколько имеющихся точек пересечения указанных мест (показать на том же примере).
4. Решение задач
1) Построить треугольник по основанию, боковой стороне и медиане, проведенной к основанию (пересечение ГМТ №1 и №2).
2) Постройте равнобедренный треугольник по основанию и радиусу описанной окружности (пересечение ГМТ №9 и описанной окружности, центр которой – ГМТ №11).
3) Построить окружность данного радиуса, проходящую через две данные точки (пересечение ГМТ №3 и №3).
5. Подведение итогов
Итак, что вы узнали на сегодняшнем занятии? Сформулируйте понятие ГМТ. В чем заключается метод ГМТ? Какие существуют этапы решения задач на построение? Раскройте суть каждого из этапов.
Домашнее задание: 1) Построить равнобедренный треугольник по основанию и боковой стороне. 2) Постройте ромб так, чтобы две противолежащие его вершины были в двух данных точках А и В и третья на данной окружности О. 3) Постройте окружность, которая касается сторон данного угла, причем одной из них – в данной точке.
Рекомендуемая литература: [11], [16], [18], [22].
Занятие №2
Тема: Применение метода ГМТ к решению задач на построение.
Цели: Научить применять метод ГМТ к решению задач на построение.
Краткое содержание: Повторение изученного материала, решение задач на построение, в которых используется более сложные геометрические места точек.
Рекомендуемая литература: [11], [16], [18], [22].
Занятие №3
Тема: Подобие. Метод подобия.
Цели: Повторить тему подобия фигур, сформировать понятие о методе подобия при решении задач на построение.
Краткое содержание: рассмотрение случаев, когда задача на построение решается методом подобия, суть метода подобия, решение задач, в которых размеры фигуры определяются заданием некоторого отрезка, различные случаи выбора центра подобия.
Рекомендуемая литература: [4], [11], [16].
Занятие №4
Тема: Применение метода подобия к решению задач на построение.
Цели: Научить применять метод подобия к решению задач на построение.
Краткое содержание: Повторение изученного материала, решение задач на построение, в которых размеры фигуры определяются заданием некоторого отрезка, суммы или разности отрезков.
Рекомендуемая литература: [4], [11], [16].
Занятие №5
Тема: Решение задач на построение методами ГМТ и подобия.
Цели: Научить видеть какой из методов следует применять к той или иной задаче.
Краткое содержание: Решение задач на применение различных методов: ГМТ и подобия.
Рекомендуемая литература: [4], [11], [16], [18], [20], [21], [22].
Занятие №6
Тема: Решение задач на построение методами ГМТ и подобия.
Цели: Научить применять методы ГМТ и подобия к решению более сложных задач на построение, научить видеть какой из методов следует применять к той или иной задаче.
Краткое содержание: Решение более сложных задач на построение на применение различных методов: ГМТ и подобия.
Рекомендуемая литература: [4], [11], [16], [18], [20], [21], [22].
Похожие работы
... труде - все это формирует и развивает познавательный интерес и превращает его в важный стимул учебной деятельности учащихся [20,46]. Существуют различные средства развития познавательного интереса: решение занимательных, логических задач, игра, исторические экскурсы и другие. Наиболее подробно остановимся на исторических экскурсах. Знакомство с историей науки полезно для каждого человека, а для ...
... координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных изображений. Можно выделить следующие цели изучения метода координат в школьном курсе геометрии: - дать учащимся эффективный метод решения задач и доказательства ряда теорем; - показать на основе этого метода тесную связь алгебры и геометрии; - способствовать ...
... развитие логического мышления учащихся является одной из основных целей курса геометрии. При изучении геометрии развитие логического мышления учащихся осуществляется в процессе формирования понятий, доказательства теорем, решения задач. При изучении геометрических построений, прежде всего, приходится преодолевать трудности логического порядка. В условиях школы для преодоления этих трудностей ...
... Таким образом, в современном мире необходимы информационно-коммуникационные технологии. ГЛАВА II. ОПЫТНО-ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ ПО ТЕМЕ: «ИНФОРМАЦИОННО-КОММУНИКАЦИОННЫЕ ТЕХНОЛОГИИ КАК СРЕДСТВО РАЗВИТИЯ ПОЗНАВАТЕЛЬНОГО ИНТЕРЕСА ПРИ ИЗУЧЕНИИ ЖИВОТНОГО МИРА В НАЧАЛЬНОЙ ШКОЛЕ» 2.1 Диагностика уровня развития познавательного интереса В результате изучения психолого-педагогической литературы ...

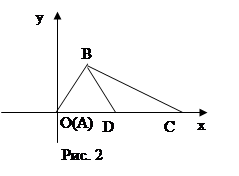





0 комментариев